王富民,倪 明,周 明,吴永政

(中国电子科技集团公司第三十二研究所,上海 201808)

0 概述

求解最大割问题是指对给定的无向加权图求取一个最大分割解,使横跨2个割集的所有边权重之和最大。最大割问题是图论中典型的NP困难组合优化问题,在图像处理[1]、信道分配[2]等工程问题中广泛存在。虽然理论上该问题可由穷举法找到最优解,但是因为运行时间随图中顶点个数或边的条数增加呈指数级增长,问题的搜索空间也急剧扩大,即使用当前最先进的计算机来计算,求解时间也极长[3]。因此,研究者一般使用近似算法计算该问题,以牺牲一定的准确率为代价来缩短运行时间[4]。

最大割问题可以通过构造简单的随机近似算法来解决。该算法随机初始化一个顶点割集,检查每个顶点,若发现某个顶点所连接的所有边中有多于一半的边的顶点属于同一子集,则将其移到另一子集中,重复寻找直到找不到此类顶点,算法终止。易证该算法最大割至少是边总数的一半,因此,其是一个0.5近似比的近似算法。Geomans-Williamson算法是著名的求解最大割问题的近似算法[5],其将半正定规划用于近似求解中,通过证明可知该算法近似比为0.878 6[6]。

在物理绝热过程中,随系统哈密顿量缓慢变化,初始系统哈密顿量的基态也会缓慢演化到最终系统哈密顿量的基态[7]。结合该定理和量子算法叠加性[8]而设计的量子绝热算法,通过设计初始哈密顿量Hb与待解问题的哈密顿量Hp之间的演化路径,构造一个缓慢变化的系统哈密顿量来求解相关问题[9-10]。

本文利用量子绝热近似算法求解最大割问题。基于Python语言的ProjectQ量子编程软件[11-13],根据图中顶点个数以及边的条数编写求解程序,其执行顺序对应于量子算法线路[14]中量子逻辑门的顺序。在此基础上,测量量子寄存器中量子比特的状态获得实验结果[15]。本文在求解最大割问题时采用线性演化路径,即初始哈密顿量的比例线性减小、最大割问题哈密顿量的比例线性增大,以提高求解准确率。

1 绝热定理与量子绝热算法

对于物理绝热过程中的哈密顿量H(t),考虑单参数s的平滑哈密顿量H*(s)(0≤s≤1),取:

H(t)=H*(t/T)

(1)

其中,T控制H(t)的变化率[16-17]。定义H*(s)的瞬时本征值Eα(s)和本征态|ψα(s)〉为:

H*(s)|ψα(s)〉=Eα(s)|ψα(s)〉

(2)

其中,α表示能级。根据绝热定理,如果最低能级之间的缝隙为:

(3)

则对于所有0 ≤s≤1严格大于0,有式(4)存在。

(4)

这意味能级间大于0的缝隙可以确保|ψα(t)〉在遵循薛定谔方程的同时,|ψα(t)〉随着t从0变化到T的过程中无限接近于|ψα(1)〉的瞬时本征态。

根据上述定理构造系统哈密顿量H(t):

H(t)=(1-t/T)Hb+(t/T)Hp

(5)

其中,Hb为易于计算出基态的初始哈密顿量,Hp为基态未知的问题哈密顿量。系统的初态为H(t=0)=Hb的基态|ψ0(0)〉,系统哈密顿量随t的增加演化到t=T时,处于终态H(t=T)=Hp的基态|ψ0(1)〉。

2 量子绝热算法求解最大割问题的理论分析

2.1 最大割问题的数学描述

设无向图G(V,E),其中,V={1,2,…,n}为顶点的集合,E⊆V×V为边的集合。

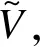
(6)

(7)

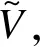
2.2 最大割问题哈密顿量的构造

对于无向图G(V,E),其中|V|=n、|E|=m表示该图有n个顶点和m条边,定义任意一个解:|Ψ〉=|ψ1〉|ψ2〉…|ψn〉,其中:

(8)

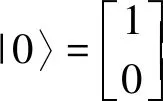
(9)

图中每条边所对应的哈密顿量为Hpei,j,定义为:

(10)

(11)

当最大割解为|z1〉|z2〉…|zn〉时,下式成立:

Hp|z1〉|z2〉…|zn〉=hmin|z1〉|z2〉…|zn〉

(12)

其中,hmin为最小本征值也是最大割解值,|z1〉|z2〉…|zn〉为基态也对应最大割解。

2.3 初始哈密顿量的构造

量子绝热算法需要从一个初始哈密顿量开始演化。这个初始哈密顿量应是简单的并且其基态也是容易获得的,定义:

(13)

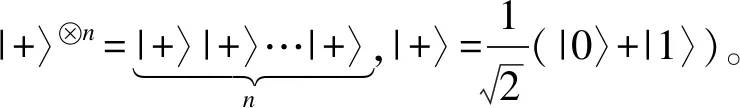
2.4 量子绝热算法逻辑线路

根据式(1)和式(5)可得:

H*(s)=(1-s)Hb+sHp

(14)

其中,s∈[0,1]单调递增,增量为Δs。

定义Ub(s)和Up(s)对应(1-s)Hb和sHp的演化算子为:

Ub(s)=e-iHb(1-s),Up(s)=e-iHps

(15)

根据具体无向图构造演化算子Up和Ub,算法描述如下:

算法1Up(graph,qureg,s)

输入最大割问题graph,待处理量子寄存器qureg,演化时间s

1.n ← graph.vertexnum

2.m ← graph.edgenum

3.edges[ ] ← graph.edges

4.hamiltonian ← 0

5.for i = 0 → m-1 do

6.subhamil[ ] ← 0

7.for j = 0 → n-1 do

8.if j ∈ edges[i] then

9.subhamil[j] ← σz(j)

10.else

11.subhamil[j] ← I(j)

12.end if

13.end for

14.hamil ← subhamil[0]

15.for k = 1 → n-1 do

16.hamil ← hamil ⊗ subhamil[k]

17.end for

18.hamiltonian ← hamiltonian+0.5(hamil-I)

19.end for

20.qureg←TimeEvolution(time=s,hamiltonian=hamiltonian)

算法2Ub(graph,qureg,s)

输入最大割问题graph,待处理量子寄存器qureg,演化时间s

1.n←graph.vertexnum

2.hamiltonian←1

3.for i=0→n-1 do

5.end for

6.qureg←TimeEvolution(time=s,hamiltonian=hamiltonian)

在该线性演化路径下可以求出最大割解|z1>|z2>…|zn>:

|z1〉|z2〉…|zn〉=

Ub(1)Up(1)…Ub(Δs)Up(Δs)Ub(0)Up(0)|+〉⊗n

(16)

演化路径对应的算法描述如下:

算法3EvolutionPath(graph,qureg,T)

输入最大割问题graph,待处理量子寄存器qureg,演化次数T

1.Δs ← 1.0/T

2.for i = 0 → T do

3.s ← i × Δs

4.Up(graph,qureg,s)

5.Ub(graph,qureg,1-s)

6.qureg.engine.flush()

7.end for

采用量子算法求解最大割问题的哈密顿量基态的过程,可用图1中量子逻辑门排列所得到的量子线路模型[18-19]表示。

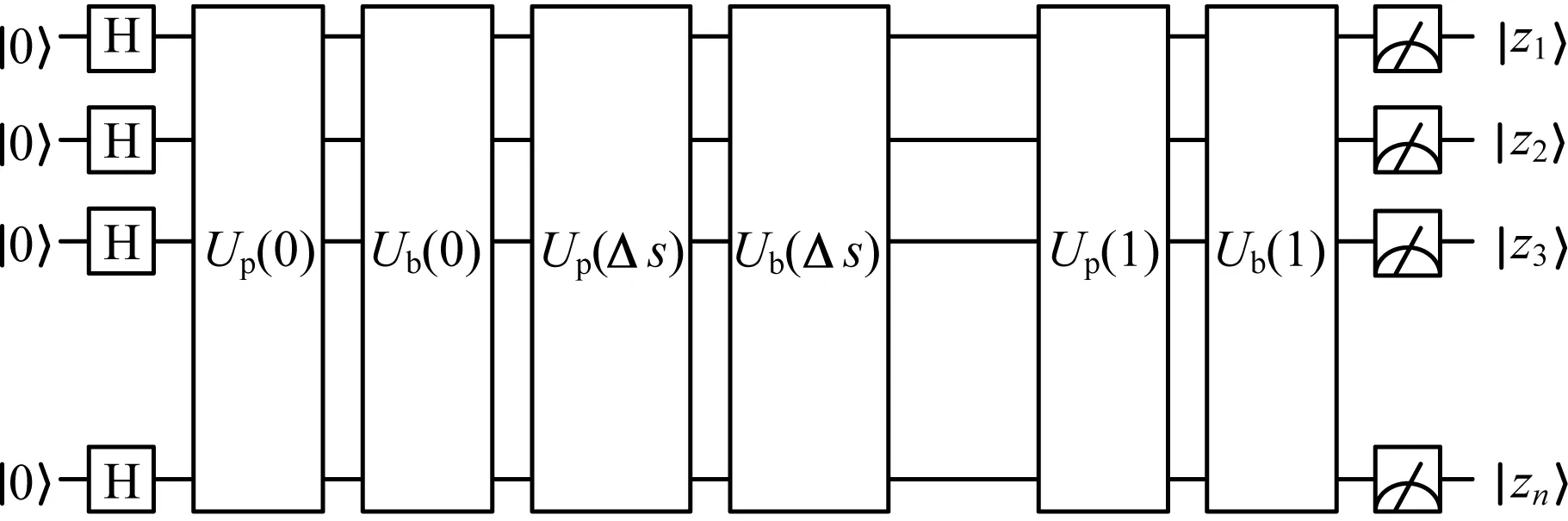
图1 最大割问题量子线路示意图

采用上述量子线路模型的量子逻辑门顺序,用ProjectQ软件框架对该算法进行模拟的伪代码如下:

算法4CreateCircuit(graph,T)

输入最大割问题graph,待处理量子寄存器qureg,演化次数T

输出graph实验结果的最优解

1.n ← graph.vertexnum

2.eng ← MainEngine(Simulator())

3.qureg ← eng.allocate_qureg(n)

4.qureg ← Tensor(H)

5.EvolutionPath(graph,qureg,T)

6.qureg ← All(Measure)

7.return qureg

3 量子绝热算法求解最大割问题的数值分析

上文给出了量子绝热算法求解最大割问题的理论模型和具体步骤,下面分别举3个顶点和6个顶点的例子,从系统哈密顿量期望值的变化曲线入手分析量子绝热算法求解最大割问题的数值结果。

3.1 3个顶点的无向图

3个顶点作为最简单的示例构建无向图,3个顶点分别标号为0、1和2,将顶点0和顶点1分别与顶点2相连构成由3个顶点2条边组成的无向连通图。如果将顶点0和1与顶点2之间的边全部切割开就会得到该图的最大割解,如图2所示。

图2 3个顶点的无向图及其最大割解

对于3个顶点的图,需要用3个量子比特|z1〉|z2〉|z3〉来表示相应顶点0、1、和2的状态。将实验最后测得量子比特状态,|0〉态标同一种颜色,|1〉态标另一种颜色。

由式(4)可得该图最大割问题的哈密顿量为:

(17)

Hp为经计算得到对角矩阵,其对角线元素依次为0、-2、-1、-1、-1、-1、-2、0。

取增量Δs=0.01,可以得到最大割问题的哈密顿量期望值〈ψ(s)|Hp|ψ(s)〉(简写为〈Hp〉)的变化曲线如图3所示。

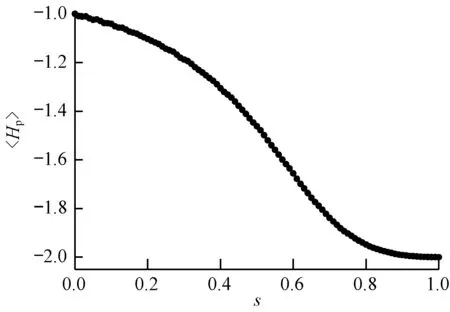
图3 3个顶点无向图最大割问题的哈密顿量期望值变化曲线

Fig.3 Expected value variation curve of Hamiltonian for max-cut problem of 3-vertex undirected graph

由图3可以看出,量子态在演化算子的作用下,从|+〉⊗3逐渐演化到最大割问题的哈密顿量基态,相应的最大割问题哈密顿量的期望值从-1平滑地下降到-2。选用哈密顿量期望的数值模拟值与理论分析的比值作为问题求解准确率,则对于该无向图最大割问题，量子绝热近似求解的准确率为0.999 9。

3.2 6个顶点的稀疏无向图

为验证量子绝热算法能够解决一些更复杂图的最大割问题,将问题规模进一步复杂化,取6个顶点,分别标号0、1、2、3、4和5,构造稀疏无向图。稀疏图即表示有很少条边(|E|≪|V|2)的图,构建稀疏图及其最大割解如图4所示。

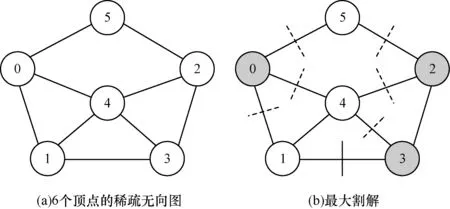
图4 6个顶点的稀疏无向图及其最大割解Fig.4 6-vertex undirected sparse graph and its max-cut solution

图4显示，对条边划分后最多有7条边被切割,因此,最大割解值为-7。同理,对于6个顶点的图需要6个量子比特来表示顶点所属集合状态。由式(10)和式(11)可得,最大割问题的哈密顿量Hp为26×26的对角矩阵,其对角元素为0、-3、-3、-4、-3、-6、-6,-7、-3、-6、-4、-5、-4、-7、-5、-6、-4、-5、-5、-4、-5、-6、-6、-5、-5、-6、-4、-3、-4、-5、-3、-2、-2、-3、-5、-4、-3、-4、-6、-5、-5、-6、-6、-5、-4、-5、-5、-4、-6、-5、-7、-4、-5、-4、-6、-3、-7、-6、-6、-3、-4、-3、-3、0。其中,-7为基态能量,对应最大割哈密顿量期望理论测量值也为-7。

对于线性演化路径下的增量Δs,分别取0.2、0.1、0.01来分析增量取值大小对最大割问题哈密顿量期望值〈Hp〉的影响,如图5所示。

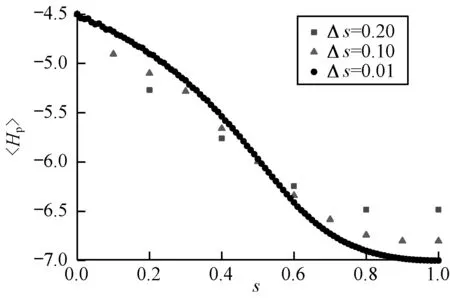
图5 不同增量Δs下6个顶点稀疏无向图最大割问题的哈密顿量期望值变化曲线

Fig.5 Expected value variation curve of Hamiltonian for max-cut problem of 6-vertex undirected sparse graph under different incremental Δs

由图5可知,当增量Δs取值越趋向于0时,演化到最终基态的最大割问题哈密顿量期望值越小,即表明有越大的概率得到最大割问题的最优解,准确率越高。对于取较大增量时,参数s从0增加到0.5时最大割问题哈密顿量的期望值有更快的下降速率,这意味着较大的增量在初期可以提高算法的效率。

当Δs=0.01时,量子绝热算法求解6个顶点稀疏图的最大割问题的准确率为0.999 9。

3.3 6个顶点的完全无向图

稠密图与稀疏图恰好相反,它是由很多条边组成的图,完全图是一种最复杂的稠密图,图中任意2个顶点之间都有边相连。将6个顶点的稀疏图扩展成完全图及其最大割解如图6所示。

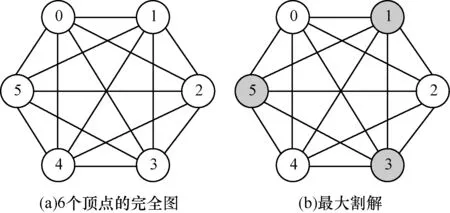
图6 6个顶点的完全图及其最大割解

Fig.66-vertex undirected complete graph and its max-cut solution

图6中共有15条边,对应最大割问题的哈密顿量Hp对角元素为0、-5、-5、-8、-5、-8、-8、-9、-5、-8、-8、-9、-8、-9、-9、-8、-5、-8、-8、-9、-8、-9、-9、-8、-8、-9、-9、-8、-9、-8、-8、-5、-5、-8、-8、-9、-8、-9、-9、-8、-8、-9、-9、-8、-9、-8、-8、-5、-8、-9、-9、-8、-9、-8、-8、-5、-9、-8、-8、-5、-8、-5、-5、0的对角矩阵,基态能量为-9,对应最大割哈密顿量期望理论测量值也为-9。根据稀疏图例子将增量Δs取0.01,对最大割问题哈密顿量的期望值〈Hp〉变化曲线如图7所示。

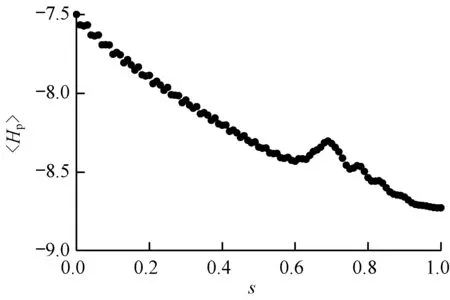
图7 6个顶点完全图的最大割哈密顿量期望值变化曲线

Fig.7 Expected value variation curve of Hamiltonian for max-cut problem of 6-vertex undirected complete graph

由图7可以看出,在参数s从0增加到1的过程中,最大割问题哈密顿量的期望值总体呈下降趋势,量子绝热算法计算出最大割问题最优解的概率较高,测量结果的准确率为0.969 6。

由于实验在设计绝热演化路径时,采用初始哈密顿量Hb与最大割问题哈密顿量Hp之间固定的参数增量Δs,并未考虑具体无向图中边与增量Δs的关系,因此,增加无向图中边的条数会降低求解最大割问题的准确率,并且得到最大割问题哈密顿量期望值的变化曲线也不再平滑[20]。

4 结束语

本文利用量子绝热算法求解无向图最大割问题,结合量子近似的思想设计算法中的演化算子,从而求解最大割问题的哈密顿量。与传统近似算法相比,该算法的时间复杂度不依赖于图的顶点个数以及边的条数,仅与增量Δs的取值相关,并可通过量子比特门的逻辑组合实现。本文列举了3个最大割问题的实例,并用ProjectQ进行编程模拟。数值分析结果表明,在顶点数较少的最大割问题中,量子绝热近似算法准确率高于文献[5]算法和随机近似算法。针对最大割问题的哈密顿量期望值随参数s变化导致曲线不平滑的问题,下一步将根据具体无向图来调整变化的增量Δs,减少无向图复杂度对计算准确率的影响。