江苏省天一中学 查晓东

无锡市第六高级中学 张 钢

前段时间，笔者在期末复习课上选择了一道经典模拟题作为典型例题，旨在引导同学们在处理解析几何问题时，关注参数选择的合理性.而所谓的“合理”也往往是仁者见仁智者见智的，恰恰就有一位同学给出了一种“奇怪”的解法.细细琢磨发现，其解法从理论上看切实可行，只是莫名其妙的产生了“增解”.笔者通过一番探究，解释了“增解”产生的原因，并由此得到了一个不错的结论，现与同学们分享.

一、探究起源

如图1，在平面直角坐标系xOy中，椭圆的右顶点和上顶点分别为A，B，线段AB的中点为M，且

（1）求椭圆的离心率；

（2）已知a=2，四边形ABCD内接于椭圆，AB∥DC.

记直线AD，BC的斜率分别为k1，k2，求证：k1·k2为定值.

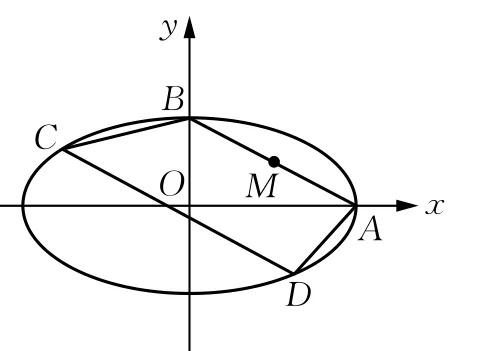
图1

1.常规视角

解析：（1）

（视角1：“设点”）设C（x0，y0），则CD代入椭圆方程整理得

2x2-2（x0+2y0）x+（x0+2y0）2-4=0，又x20+4y20=4，可得x2-（x0+2y0）x+2x0y0=0，

（视角2：“设线”）设CD将代入椭圆方程整理得

x2-2mx+2m2-2=0⇒x1+x2=2m，x1x2=2m2-2.

将x1=2m-x2代入得到（定值）.

【评注】视角1巧妙地利用点在椭圆上，将x20+4y20=4作为整体，视角2则巧妙地利用x1与x2的关系进行替换，根据分母的结构进行配凑，应该说这两种方法是参数的“合理”选择.然而，一个学生给出了如下解法：

2.“奇怪”视角

解析：（2）假设直线AD，BC的方程分别为y=k1（x-2），y=k2x+1，D（x1，y1），C（x2，y2），

将AD方程代入椭圆方程得x2+4k21（x-2）2=4⇒（1+4k21）x2-16k21x+16k21-4=0，解得

将BC方程代入椭圆方程得x2+4（k2x+1）2=4⇒（1+4k22）x2+8k2x=0，解得

所以32k21k22+16k1k2（k1-k2）+4k2-4k1-2=0⇒（4k1k2-1）[4k1k2+2（k1-k2）+1]=0，

所以4k1k2-1=0或4k1k2+2（k1-k2）+1=0.

【评注】上述解法看似十分“暴力”，其实根据“设而且求”的思想将C，D两点的坐标分别用k1，k2来表示，最后利用来找到k1，k2的关系，也应该算是一种“合理”的解法.只是为何产生4k1k2+2（k1-k2）+1=0这个“增解”，着实费了一番功夫.

经过思考，笔者发现-32k21k22-32k21k2-8k21+8k22-8k2+2=-2[4k1k2+2（k1-k2）+1]·[4k1k2+2（k1+k2）-1]，这样就不难解释为什么4k1k2+2（k1-k2）+1≠0了，换言之，上述解法进行了不等价变形.至此，学生提出的疑惑得以解决.然而，笔者却意犹未尽，进一步探究发现当4k1k2+2（k1-k2）+1=0时，C，D两点重合，相信这绝非偶然，因此笔者给出了如下结论.

二、探究结果

考虑到：椭圆上任意一点P与椭圆长轴的两个端点A，B（点P异于A，B）有kAP·kBP为定值，当A，B为短轴的两个端点时，结论也成立.我们可以联想，当A与B，一个为长轴端点，另一个为短轴端点时，是否会有类似的结论呢？

结论：如图2，A，B分别为椭圆的右顶点与上顶点，P为椭圆上任意异于A，B的一点，设直线AP，BP的斜率分别为k1，k2，则

证明：设P（x0，y0），则

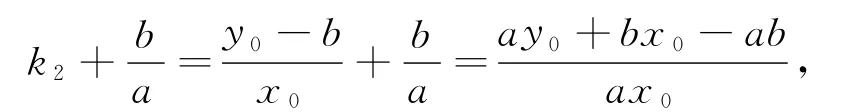
将a2y20=a2b2-b2x20代入，

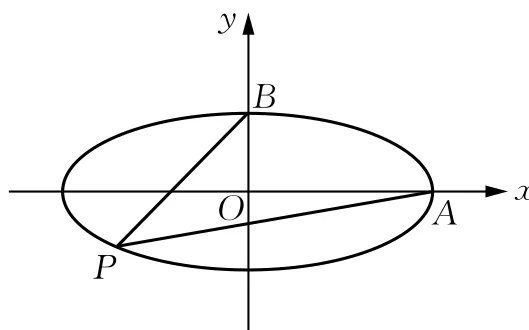
图2

【评注】类似地，我们还可以得到：①当A，B分别为椭圆的左顶点与下顶点时，有相同的结论；②当A，B分别为椭圆的右顶点与下顶点（或者A，B分别为椭圆的左顶点与上顶点）时，有

双曲线中是否存在类似的结论呢？有兴趣的同学可以尝试探究.

三、结语

古云“学而不思则罔，思而不学则殆”，同学们要学会用数学眼光观察世界，用数学思维分析世界，用数学语言表达世界.在笔者看来，同学们解题不仅需要“仰视”，也需要“俯视”.

1.解题视角替代不了解题经验

本文中谈及的例题恰恰是站在“参数的合理选择”的视角来总结处理解析几何问题的方法.然而，要真正驾驭这些方法，同学们除了对方法有深层次的理解，还需要有大量的解题经验，以及各种解题视角下的不断尝试、失败、再尝试.正所谓“操千曲而后晓声，观千剑而后识器”，讲的就是“仰视”的道理.

2.解题反思丰富解题经验

本文“奇怪”视角中谈及的“增解”产生的原因说明：在解题过程中，同学们需要时刻关注代数式结构转换的等价性.必要的解题回顾与反思也就是“俯视”，不仅能加深同学们对问题的本质及其解法的进一步理解，同时也能够培养同学们解题的科学与严谨.