■张文伟

题型一：二分法求函数零点

二分法只适用于变号零点，二分法是求方程的根的近似值的一种方法。其记忆口诀是：定区间，找中点，中值计算两边看，同号去，异号算，零点落在异号间，周而复始怎么办，精确度上来判断。

例1用二分法求函数f（x）=ln（x+1）+x-1在区间[0，1]上的零点，要求精确度为0.01时，所需二分区间的次数最少为（ ）。

A.5 B.6

C.7 D.8

解：开区间（0，1）的长度等于1，每经过一次操作，区间长度变为原来的一半，经过n次操作后，区间长度变为因为用二分法求函数f（x）=ln（x+1）+x-1在区间[0，1]上的近似解，要求精确度为0.01，所以0.01，解得n≥7。应选C。

跟踪训练1：用二分法求图像连续不断的函数f（x）在（1，5）上的近似解（精确度为0.1），求解的部分过程如下：f（1）·f（5）＜0，取（1，5）的中点，计算得f（1）·f（x1）＜0，f（x1）·f（5）＞0，则此时能判断函数f（x）一定有零点的区间为

提示：因为f（x）为图像连续不断的函数，且f（1）·f（3）＜0，所以函数f（x）在区间（1，3）内一定有零点。

题型二：函数零点所在区间的判断

确定函数f（x）的零点所在区间的两种常用方法：（1）定义法：使用零点存在性定理，函数y=f（x）必须在区间[a，b]上是连续的，当f（a）·f（b）＜0时，函数在区间（a，b）内至少有一个零点。（2）图像法：若一个函数（或方程）由两个初等函数的和（或差）构成，则可考虑用图像法求解，如f（x）=g（x）-h（x），作出y=g（x）和y=h（x）的图像，其图像交点的横坐标即为函数f（x）的零点。

例2函数的零点所在的大致区间是（ ）。

A.（0，1） B.（1，2）

C.（2，3） D.（3，4）

解：因为f（1）=ln2-2＜0，f（2）=ln3-1＞0，所以由零点存在性定理可得零点所在的大致区间是（1，2）。应选B。

跟踪训练2：设f（x）=lnx+x-2，则函数f（x）的零点所在的区间为（ ）。

A.（0，1） B.（1，2）

C.（2，3） D.（3，4）

提示：（方法1）因为f（1）=0+1-2=-1＜0，f（2）=ln 2+2-2=ln2＞0，所以函数f（x）的零点所在区间为（1，2）。应选B。

（方法2）函数f（x）的零点所在的区间可转化为函数g（x）=lnx与h（x）=-x+2的图像交点的横坐标所在的取值范围。作出两个函数的图像，如图1所示。

由图1可知，函数f（x）的零点所在的区间为（1，2）。应选B。

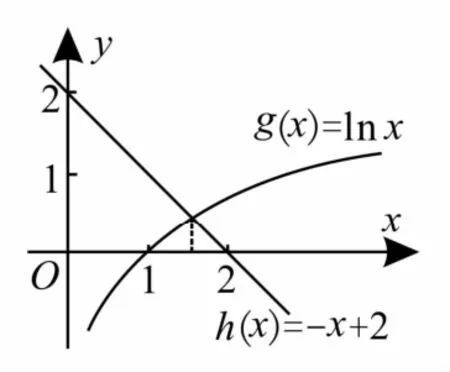
图1

题型三：判断函数零点的个数

判断函数零点个数的三种方法：（1）方程法：令f（x）=0，如果能求出解，则有几个解就有几个零点。（2）零点存在性定理法：利用定理不仅要求函数在区间[a，b]上是连续不断的曲线，且f（a）·f（b）＜0，还必须结合函数的图像与性质（如单调性、奇偶性、周期性、对称性）才能确定函数有多少个零点或零点所具有的性质。（3）数形结合法：转化为两个函数图像的交点个数问题，先画出两个函数的图像，看其交点的个数，其中交点的横坐标有几个不同的值，就有几个不同的零点。

例3函数f（x）=|x-2|-lnx在定义域内的零点的个数为（ ）。

A.0 B.1

C.2 D.3

解：由题意可知f（x）的定义域为（0，+∞）。在同一直角坐标系中画出函数y=|x-2|（x＞0）和y=lnx（x＞0）的图像，如图2所示。

图2

由图2可知，函数f（x）在定义域内的零点个数为2。应选C。

跟踪训练3：已知分段函数f（x）=（为自然对数的底数），则e函数y=f[f（x）]-f（x）的零点个数为（ ）。

A.2 B.3

C.4 D.5

提示：令u=f（x），对函数y=f[f（x）]-f（x）求零点。由f（u）-u=0，可得解得u=e或u=-2。

当u=e时，由f（x）=e，可得或易得共有3个解;当u=-2时，由可 得或易得共有 个解。2

综上可知，所求方程共有5个解，即所求函数有5个零点。应选D。

题型四：函数零点中的含参数问题

已知函数有零点（方程有根）求参数取值范围的三种常用方法：（1）直接法：根据题设条件构建关于参数的不等式，通过解不等式确定参数的范围。（2）分离参数法：将参数分离，转化成求函数值域问题加以解决。（3）数形结合法：先对解析式变形，在同一平面直角坐标系中画出函数的图像，利用图像求解。

例4已知在区间（0，2]上的函数f（x）且g（x）=f（x）-m x在区间（0，2]上有且仅有2个不同的零点，则实数m的取值范围是（ ）。

解：函数g（x）=f（x）-m x在（0，2]上有且仅有2个不同的零点，即函数y=

f（x）与y=m x在（0，2]上的图像有且仅有2个不同的交点。作出函数y=f（x）与y=m x的图像，如图3所示。

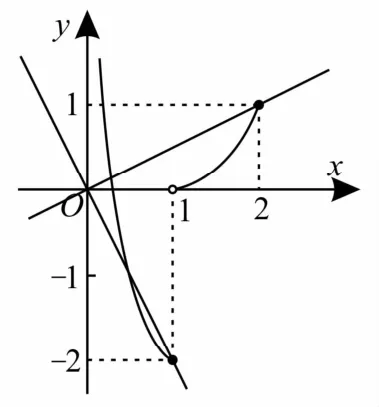
图3

跟踪训练4：已知函数f（x）=，若函数f（x）在R上有2个零点，则实数a的取值范围是（ ）。

图4

提示：画出函数f（x）的大致图像，如图4所示。

因为函数f（x）在R上有2个零点，所以f（x）在（-∞，0]和（0，+∞）上各有一个零点。当x≤0时，f（x）有一个零点，需满足1-a≥0，即a≤1;当x＞0时，f（x）有一个零点，需满足-a＜0，即a＞0。综上可知，0＜a≤1。应选A。

题型五：函数零点中的新定义问题

对于这类问题，首先要弄清楚新定义的含义，再根据函数的性质来解答。

例5用[a]表示不大于实数a的最大整数，如[1.68]=1，设x1，x2分别是方程x+ex=4，x+ln（x-1）=4的根，则[x1]+[x2]

解：因为x1，x2分别是方程x+ex=4和x+ln（x-1）=4的根，所以x1，x2分别是函数g（x）=x+ex-4和h（x）=x+ln（x-1）-4的零点。

由g（x）是单调递增函数，且g（1）＜0，g（2）＞0，可得1＜x1＜2。由h（x）在定义域内单调递增，且h（3）＜0，h（4）＞0，可得3＜x2＜4。由上可得[x1]=1，[x2]=3，故[x1]+[x2]=4。

跟踪训练5：设函数f（x）=1+[x]-x，其中[x]表示不超过x的最大整数，若函数y=logax的图像与函数f（x）的图像恰有3个交点，则实数a的取值范围是（ ）。

A.[2，3） B.（2，3]

C.（3，4] D.[3，4）

提示：f（x+1）=1+[x+1]-（x+1），

而[x+1]=[x]+1，故f（x+1）=1+[x+1]-（x+1）=1+[x]+1-x-1=1+[x]-x=f（x），即函数f（x）的周期为1。

当x∈[0，1）时，f（x）=1-x，由此可得f（x）在[0，+∞）上的图像，如图5所示。

图5

因为y=logax的图像与y=f（x）的图像有3个交点，故可得3≤a＜4。应选D。

题型六：复合函数的零点问题

求复合函数y=f[g（x）]的零点问题可转化为解方程问题。令f[g（x）]=0，可得f（t）=0和g（x）=t，先从方程f（t）=0中求出t，再代入方程g（x）=t中求出x的值。

例6设函数则函数y=f[f（x）]-1的零点个数为

解：①当x≤0时，y=f[f（x）]-1=f（2x）-1=log22x-1=x-1，令x-1=0，则x=1，显然与x≤0矛盾，可知当x≤0时，y=f[f（x）]-1无零点。

②当x＞0时，分两种情况讨论：当x＞1时，log2x＞0，y=f[f（x）]-1=f（log2x）-1=log2（log2x）-1，令log2（log2x）-1=0，得log2x=2，解得x=4;当0＜x≤1时，log2x≤0，y=f[f（x）]-1=f（log2x）-1=2log2x-1=x-1，令x-1=0，解得x=1。

综上可知，函数y=f[f（x）]-1的零点个数为2。

跟踪训练6：已知函数f（x）=则函数F（x）=f[f（x）]-f（x）-1的零点个数是

提示：令f（x）=t，则函数F（x）=f[f（x）]-f（x）-1的零点个数问题⇔f（t）-t-1=0的根的个数问题。画出函数y=f（t），y=t+1的简图，如图6所示。

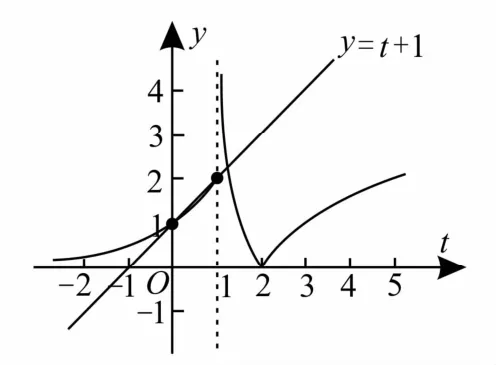
图6

结合图像可得f（t）-t-1=0的根为t1=0，t2=1，t3∈（1，2）。方程f（x）=0有1个解，f（x）=1有3个解，f（x）=t3有3个解。综上可知，函数f（t）-t-1=0的零点个数是7。

题型七：利用所给函数模型解决实际问题

求解所给函数模型解决实际问题的几个关注点：（1）认清所给函数模型，弄清哪些量为待定系数。（2）根据已知条件，利用待定系数法确定模型中的待定系数。（3）利用该模型求解实际问题。

例7某公司为激励创新，计划逐年加大研发资金投入，若该公司2017年全年投入研发资金130万元，在此基础上，每年投入的研发资金比上一年增长12%，则该公司全年投入的研发资金开始超过200万元的年份是（ ）。

A.2020年 B.2021年

C.2022年 D.2023年

解：由题意求满足130（1+12%）n-1＞200的最小n值。

由 130（1+12%）n-1＞200，可 得l g[130（1+12%）n-1]＞l g200，所以l g 1.3+2+（n-1）l g1.12＞l g2+2，即 0.11+0.05（n-1）＞0.3，所以n＞4.8，所以nmin=5，可知开始超过200万元的年份是2017+5-1=2021。应选B。

跟踪训练7：将甲桶中的am3水缓慢注入空桶乙中，tm i n后甲桶剩余的水量符合指数衰减曲线y=aen t。假设过5m i n后甲桶和乙桶的水量相等，若再过mm i n甲桶中的水只有，则m的值为（ ）。

A.5 B.8

C.8 D.10

提示：根据题意，因为5m i n后甲桶和乙桶的水量相等，所以函数y=f（t）=aen t满足，可得，因此当km i n后甲桶中的水只有可得f（k）=，所以，解得k=10。故k-5=5（m i n），即得m=5m i n。应选A。

题型八：构建函数模型解决实际问题

构建函数模型解决实际问题的常见类型与求解方法：（1）构建二次函数模型，常用配方法、数形结合法求解。（2）构建分段函数模型，应用分段函数分段求解的方法。（3）构建指数函数、对数函数和幂函数模型解决实际问题的关键是理解三种函数的图像与性质。

例8加工爆米花时，爆开且不煳的粒数占加工总粒数的百分比称为“可食用率”。在特定条件下，可食用率p与加工时间t（单位：m i n）满足函数关系p=a t2+b t+c（a，b，c是常数），图7记录了三次实验的数据。根据上述函数模型和实验数据，可以得到最佳加工时间为

图7

解：由题意可得函数p=a t2+b t+c（a，b，c是常数）经过点（3，0.7），（4，0.8），（5，0.5），代入此方程解得a=-0.2，b=1.5，c=-2，这时函数p=-0.2t2+1.5t-2=-0.2（t-3.75）2+0.8125。故得到最佳加工时间为3.75m i n。

跟踪训练8：某单位为鼓励职工节约用水，作出如下规定：每位职工每月用水不超过10m3，按每立方米3元收费;用水超过10m3的，超过的部分按每立方米5元收费。某职工某月的水费为55元，则该职工这个月实际用水为（ ）。

A.13m3B.14m3

C.15m3D.16m3

提示：设该职工这个月的实际用水为xm3，水费为y元。由题意可得y=于是整理可得=y易知该职工这个月的实际用水量超过10m3，所以5x-20=55，解得x=15。应选C。