■傅红玲 陈立明

本文对函数应用中的创新问题的求解方法进行归纳总结，希望对同学们求解创新问题有所帮助与启迪。

创新1：函数最大值与最小值之和中的整体思维

例1已知函数f（x）=ln（x+的最大值和最小值分别是M和m，则M+m=

解：利用指数作为变量的分式函数和对数的复合函数，研究奇偶性和单调性确定其最值。由[-k，k]，可知g（x）为增函数，可得g（-k）≤g（x）≤g（k），g（-k）+g（k）=，即g（x）关于点（0，2）对称，而由h（x）=ln（x+可知h（x）为奇函数且为增函数，可得h（-k）≤h（x）≤h（k），且h（-k）+h（k）=0。故M+m=f（k）+f（-k）=g（k）+h（k）+g（-k）+h（-k）=g（-k）+g（k）+h（-k）+h（k）=g（-k）+g（k）=4。

升华：本题实质上是求递增的奇函数与递增的中心对称函数构成的复合函数在对称区间上的最大值与最小值的和。研究两个函数的对称性、单调性以及树立整体思维的意识是求解的关键。

创新2：由函数的值域探究其定义域

例2设分段函数f（x）=若函数f（x）在区间[m，4]上的值域为 [-1，2]，则实数m的取值范围为

解：由函数的值域探究其定义域，可利用数形结合法切入。作出函数f（x）的图像，如图1所示。

图1

当x≤-1时，函数单调递减，且最小值为令，解得x=-8;当x＞-1时，函数在（-1，2）上单调递增，在[2，+∞）上单调递减，其最大值为2，且

结合函数图像可得所求实数m的取值范围为

升华：由函数值域探究其定义域系逆向思维，利用定义域到值域唯一的对应关系，借助函数图像和特殊函数值处的自变量的取值，以形助数和运动变化的观念是探究其定义域的关键。

创新3：自变量与函数值求和中的整体思维

例3已知函数g（x）对任意的x∈R，都有成立g（x）的图像有m个交点…，（xm，ym），则

解：探究两个函数的对称中心是解题的切入点。由题设，令t=2x-2013，则2018-2x=5-t，可得g（5-t）=3-g（t），可知y=g（x）的对称中心为由f（x）=，可知y=f（x）的对称中心为据此可知y=f（x）与的图像有m个交点关于点中心对称，所以x1+xm=x2+xm-2=x3+xm-3=…=5，y1+ym=y2+ym-2=y3+ym-3=…=3。

设x1+x2+…xm-1+xm=M，则xm+xm-1+…+x2+x1=M，两式相加可得

升华：利用换元法探究函数图像的对称中心是本题的一个创新;求两个函数交点的自变量与函数值的和，探究两个函数的同一对称中心，利用整体思维的意识简化求解是本题的又一个创新。

创新4：函数不等式中的合理转化

例4已知函数f（x）=2x且f（x）=g （x）+h（x），其中g （x）为奇函数，h（x）为偶函数，若不等式3a g （x）+h（2x）≥0对任意的x∈[1，2]恒成立，则实数a的取值范围是

解：由已知得g （x）+h（x）=2x，注意g （x）为奇函数，h（x）为偶函数，则g（-x）+h（-x）=2-x，即-g（x）+h （x）=2-x。由此解得，代入不等式3a g（x）+h（2x）≥0，可知在[1，2]上恒成立。

令t=2x-2-x，则可得22x+2-2x=t2+2。

故上述不等式可转化为3a≥可知函数在上单调递减，当取得最大值为由此可得，即a∈

升华：利用奇偶性构建方程组，求待定解析式是本题的一个创新;把函数不等式问题合理转化为含指数变量的不等式恒成立问题是本题的又一个创新。本题的解题过程凸显函数不等式中的合理转化思想。

创新5：新定义的图像交点问题

例5若点A，B分别是函数y=f（x）与y=g（x）的图像上的点，且线段A B的中点恰好为原点O（0，0），则称A，B为两个函数的一对“孪生点”。若函数f（x）=l g|x|，g（x）=2x，则这两个函数的“孪生点”共有（ ）。

A.1对 B.2对

C.3对 D.4对

解：由题意可知“孪生点”为y=f（x）与y=g（x）的交点且交点关于原点对称，因此也就是求y=f（x）与y=-g（-x）的交点个数。由g（x）=2x，得-g（-x）=-2-x=，画出与y=l g|x|的图像，如图2所示。

图2

由图2可知，两个函数图像有2个交点，所以f（x）=l g|x|与g（x）=2x这两个函数的“孪生点”共有2对。应选B。

升华：解答新定义的函数图像交点问题的关键是弄清新定义的含义，按新定义的要求，“照章办事”，逐条分析、验证、运算。本题通过定义两个函数的“孪生点”达到考查对数函数、指数函数的图像以及函数图像的对称变换的目的。

创新6：超越方程中的最值问题

例6已知方程2018x=a-x和方程log2018x=a-x（a＞1）的根分别为x1，x2，则的取值范围为（ ）。

解：注意到两个方程的特征，利用同底数的指数函数与对数函数的图像关于直线y=x对称以及根的意义为切入点，构建二次函数在区间上的最值求解。由题意可知y=2018x与y=log2018x互为反函数，其图像关于直线y=x对称。由可得交点坐标满足于是恒有x+x=2×12设0＜x1＜x2，则，所以注意到函数g（x1）在区间上单调递减，于是可得g（x1）＜g（0）=a2。应选B。

升华：利用互为反函数的图像关于直线y=x对称，探究两根的关系，选择主元挖掘隐含条件，构建函数求解取值范围问题。解答本题的关键是如何缩小主元的取值范围，如由对称性及隐含条件可得

创新7：复合函数中的不等式问题

例7已知分段函数f（x）=则不等式f（2x2-|x|）≤5的解集为

解：作出分段函数的图像，利用函数的单调性求解。

当x＜0时，f（x）=-x2+x+1=且函数为增函数;当x≥0时且函数为增函数。画出分段函数f（x）的图像，如图3所示。

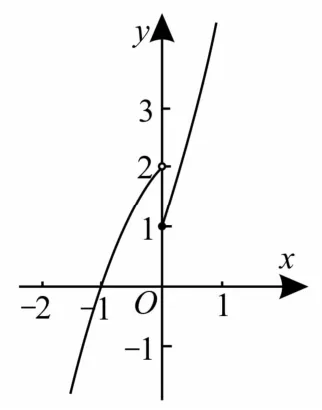
图3

因为f（1）=5，所以不等式f（2x2-|x|）≤5等价于则，即解得或，所以

升华：解答复合函数中的不等式问题的关键是树立“整体变量”观念的应用意识。解题时，作出分段函数的图像便于寻找分界点和单调性。