Manipulating transition of a two-component Bose–Einstein condensate with a weak δ-shaped laser∗
2019-11-06BoLi李博XiaoJunJiang蒋小军XiaoLinLi李晓林WenHuaHai海文华andYuZhuWang王育竹
Bo Li(李博), Xiao-Jun Jiang(蒋小军), Xiao-Lin Li(李晓林),†,Wen-Hua Hai(海文华), and Yu-Zhu Wang(王育竹)
1Key Laboratory for Quantum Optics,Shanghai Institute of Optics and Fine Mechanics,Chinese Academy of Sciences,Shanghai 201800,China
2University of Chinese Academy of Sciences,Beijing 100049,China
3Department of Physics and Key Laboratory of Low-dimensional Quantum Structures and Quantum Control of Ministry of Education,Hunan Normal University,Changsha 410081,China
Keywords:two-component Bose–Einstein condensate,quantum kicked top model,nonclassical state
1.Introduction
The two-mode quantum system is a basic model to study the transition dynamics in quantum physics. With the experimental realization of the double-well Bose–Einstein condensate(BEC)[1]and the two-states BEC,[2,3]these ultracold atoms are an ideal platform for studying and manipulating transition dynamics and entanglement of atoms on a macroscopic scale.[4]Different from the single-atom system,the transition dynamics of the many-body BEC system are remarkably affected by collision interactions.[5]This nonlinear interaction has been found to play an important role in nonlinear Josephson oscillation,[6–8]nonlinear Landau–Zener tunneling,[9–12]nonlinear Rosen–Zener tunneling,[13,14]and coherent destruction of tunneling(CDT),[15,16]and affects the generation of many-body entangled states.[17–19]
In recent years,periodic modulation technique has been frequently used for controlling the transition dynamics of the BEC systems.For example,researchers proposed two ways to precisely control the number of bosons allowed to tunnel in a double-well BEC system by periodically modulating the collision interactions[15]and the external force,[16]respectively.The δ-shaped periodic kick,which is a specific periodic modulation,exhibits a series of dynamical phenomena in chaos research,such as quantum chaos owing to the existence of the two-body interaction,[20,21]the emerging field of the excited-state quantum phase transition owing to dynamic instability,[22]and the quantum resonance.[23–25]Recently,the δ-shaped kick was realized with a pair of frequency combs and was used to manipulate the transition dynamics of a single atomic qubit[26]and the entanglement[27,28]of two-atomic qubits.But it remains a difficult task to precisely control the transition(tunneling)in a many-body system.
In this work,we investigate the transition dynamics of the BEC with two internal states driven by weak and periodic δ-shaped laser pulses.The same as the treating in the chaos research,we deal with this system in a quantum kicked top model. Adopting the perturbation method,we find that the transition probability is small in the general case due to the weak pulse intensity,but in some special cases the weak laser pulses could cause resonance and lead to transition.Using this special resonance phenomenon,we propose a scheme to control the atom numbers to be odd or even which is independent of the atom number. We also propose a scheme to obtain a desired number of atoms by tuning the parameters to be atom number dependent.
2.Theoretical model and solution
We consider a two-mode BEC system that consists of N87Rb atoms with two hyperfine statesand[3]The atoms are trapped in a single well and the two levels are coupled through the laser-induced Raman transition. In the form of second quantization,the Hamiltonian of the system can be given as follows:[29,30]
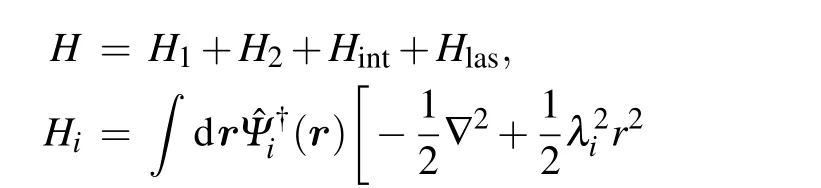
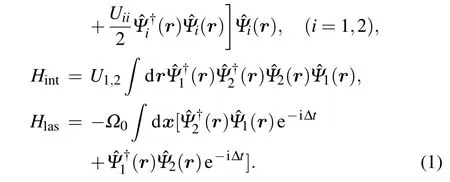
The above Hamiltonian has been rescaled by an appropriateand all the variables are dimensionless.[29]describes the Hamiltonian of the atoms in statesandin the absence of the interactionsbetween atoms in different internal states.represents the laser-induced coupling with a Rabi frequency Ω0and a laser detuning ∆.The Rb atoms are confined in a harmonic trap at frequencies λi.describe the interaction strengths of the intra-component and inter-component two-body collisions,with the corresponding s-wave scattering lengthsand the length of the harmonic oscillatorThe field operatorsandannihilate and create atoms at r in states,and satisfy the commutation relationFor simplicity,we assume the scattering lengths satisfy
To focus on the population change in the two internal levels and neglect the external motion of the atoms,we take a two-mode approximationwhere a1and a2are the annihilation operators of statesandrespectively,and obey the commutation relationsandexpresses the spatial and normalized mode functions. The two-mode approximation performances well when the scale of the condensate is small,otherwise the atoms will not stay in the ground state of the harmonic oscillator because of the collisional interactions and the two-mode approximation breaks down.As shown in Ref.[31],the number of the atoms should satisfy the conditionwhere r0is the position uncertainty in a harmonic oscillator ground state.After dropping the c-number terms as the total number of the atoms,is conserved,the two-mode Hamiltonian becomes[30]
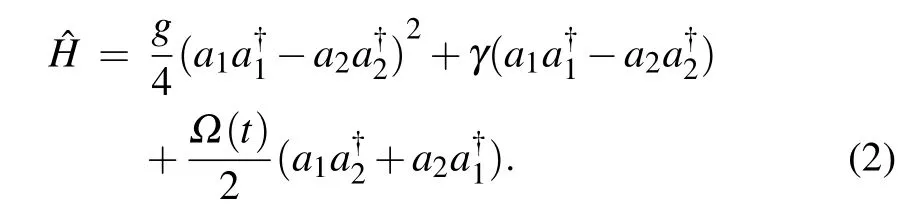
Here the effective nonlinearity g=u11+u22−2u12, the effective detuningand the coupling strengthwithandIf we switch the coupling laser on and off rapidly and periodically,Ω(t)will take the form of δ-function pulse[32]

Here the evolution time t and the pulse separation T are the dimensionless variables in units of 1/ω0and the pulse width σ →0,while σΩ0remains finite.Moreover,we reduce the Hamiltonian to a simpler form by employing an angular momentum representation
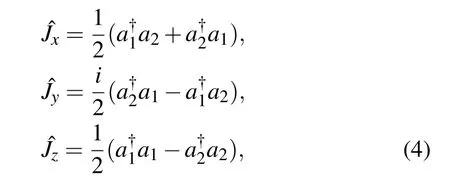
which obeys the usual angular momentum commutation relations and fulfillsFinally,we obtain a Hamiltonian in the form of a nonlinear quantum top model

The previous works toward this quantum kicked model were mostly focused on quantum entanglement,chaos,[33,34]and dynamical instability.[20,22]Generally,the iterated mapping method is preferred for solving this model.[35–38]However,this iterated mapping method,which has frequently been used for the chaos problem,loses quantum characteristics,such as the eigenfunction and the eigenenergy,[35]which are very important for controlling the atoms precisely. Differently,we attempt to study the transition dynamics of this model using a perturbation method as shown in Ref.[39].
Assuming a weak laser coupling,we study the transition probability of the atoms among different eigenstates(l=N/2,m=−l,−l+1,...,l)of the angular momentum component Jzthrough a time-dependent perturbation method.According to the perturbation theory,we divide the Hamiltonian into two partswhere the timeindependent part isand the time-dependent perturbation isNext,we carry out perturbation expansion of the state vector as
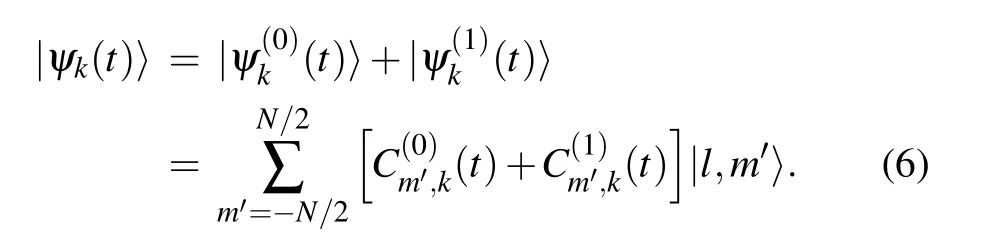
Here the letter k labels the initially occupied state,and superscripts(0)and(1)indicate the perturbation orders.Clearly,satisfeis the time-dependentequationIt is easy to obtain the wave function of the zeroth order as Such a state is an eigenstate of H0with eigenenergy Ek=γk+gk2.Next,we solve the first-order equationwhich is equivalent to
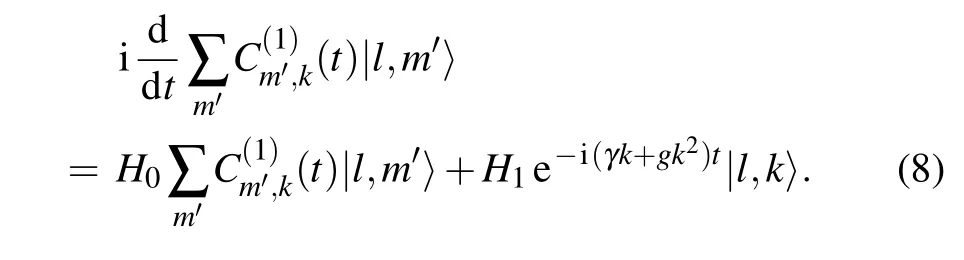
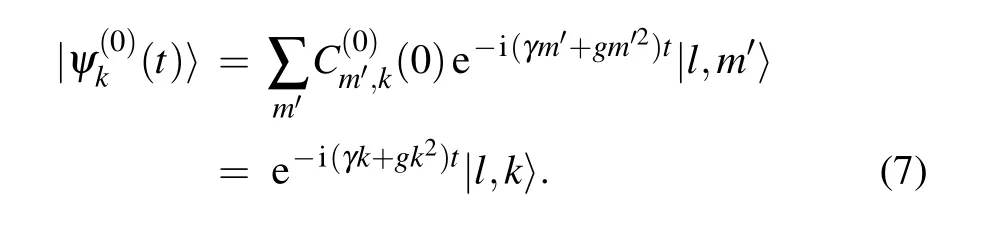
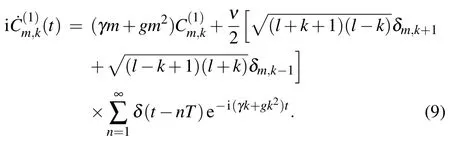
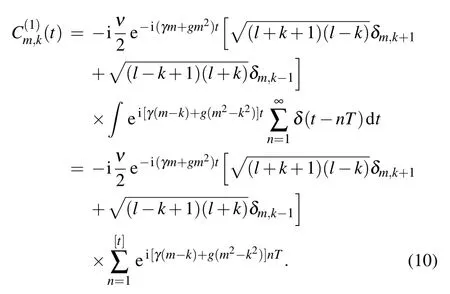
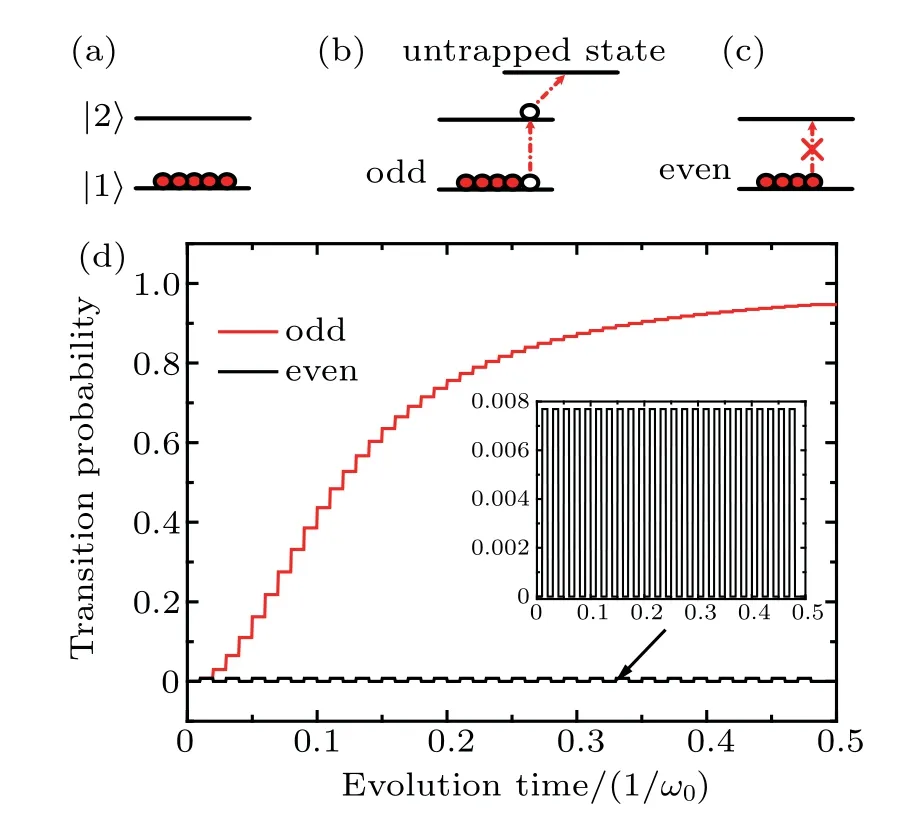
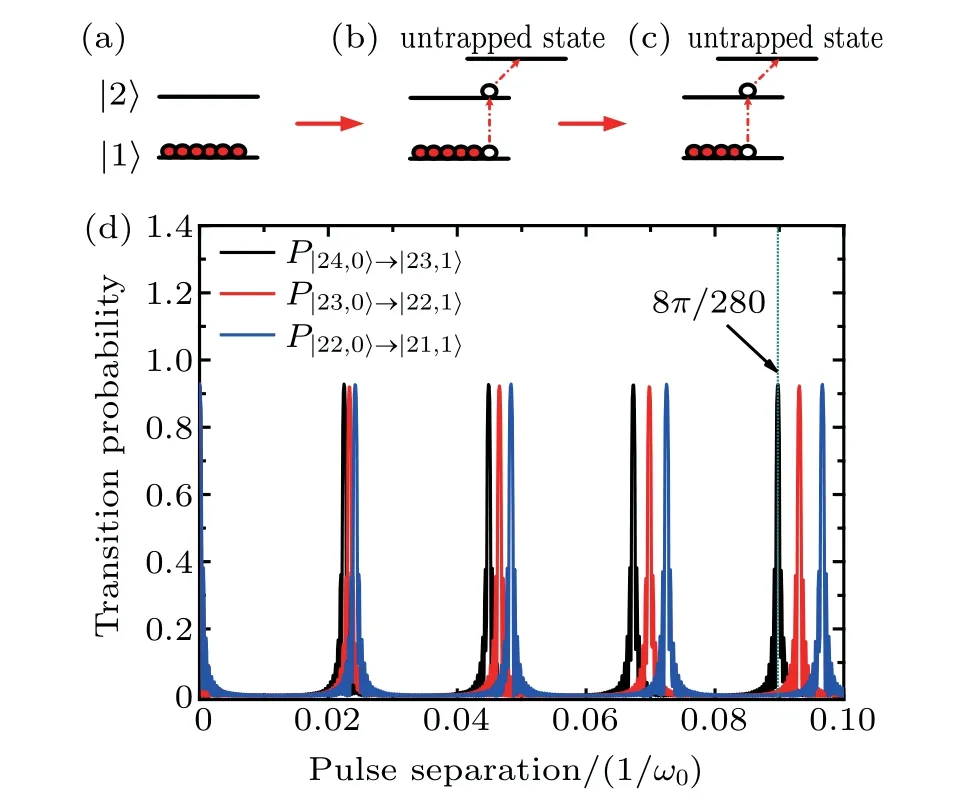
Here[t]denotes an integer obeying[t]≥1 and t −1<[t] The corresponding transition probabilities read From Eq.(12),one can conclude that the following condition has to be satisfied to make the transition probability grow with the kick numbers adds: where n±is integer.As shown in Fig.1(a),the transition probability will lead to resonance when the parameters meet the resonance condition(different peaks relate to different values of n±).Additionally,the resonance conditions of the transition between different angular momentum eigenstates are diverse because they are k-dependent.The specific evolution process of the transition probability is shown in Fig.1(b).When the resonance condition is satisfied,the transition probability increases monotonically with the kick time.Otherwise,it will oscillate periodically and remain to be a negligible value.It should be noted that the resonance condition ofis equal toaccording to the first-order time-dependent perturbation theory.Therefore,the system could evolve back from stateif the transitionis allowed. Fig.1. (a)The transition probabilities of P9,10(black line)and P8,9(red line)after 50 kicks with N=20,ν=0.01,γ=50,and g=10.(b)The specific evolution processes of the transition probabilities with T=2π/240(resonant situation)and T=0.04(off-resonant situation)respectively(assuming a trap frequency ω0 of 2π×10 kHz).Pj,i expresses the probability of transiting from initial statetoand all the variables are dimensionless. Quantum transition between stationary states is a basic problem in quantum mechanics.The idea of resonance transition is associated with the driving frequency fitting a level difference between two internal electronic states[40]or two external motional states.[41–44]But,additional resonance condition is required to allow the transition to happen when the coupling strength is weak.Quantum chaos studies determined the resonance condition of a linear kick-rotor system aswith ω±denoting the energy difference of the vibrational levels and n±being the positive rational numbers.[45]Recall the eigenenergy Ek=γk+gk2,we have the level differences Here,the resonance condition allowing the transition between different angular momentum eigenstates is similar to that in the quantum chaos case,but with n±being an integer. It is well known that the state vector of a Hamiltonian system(5)also can be expressed by the Fock baseswith Ni(i=1,2)being the number of atoms occupying the i-th internal hyperfine state.Employing the equationsand N1+N2=N,we fnidandThis means that the initial and final statescorrespond to the Fock statesConsequently,the transitions fromtoare equivalent to those fromwhich means an atom jumps between the two internal levels.For the resonance case,we list two types of resonance parameters as follows. Although the resonant condition is k-dependent as shown in Eq.(13),this dependence could be removed in some special cases.Considering the parameters fulfill a special condition where n1and n2are integers, we find three types of kindependent resonances: 1)If n1and n2are both even,all transitions between different angular momentum eigenstates are resonant,which means every atom is allowed to transition.2)If n1and n2are both odd,the resonance condition is fulfilled when 2k=N1−N2is even,i.e.,the transition is allowed when the population difference is even.3)Similarly,if n1is even and n2is odd,the resonance condition is fulfilled when the population difference is odd.Based on this unique phenomenon,we can control whether the number of atoms is even or odd. As an example,we consider a two-level BEC with all the atoms prepared in statei.e.,the Fock stateat first(as shown in Fig.2(a)). Secondly,we shine a continuous laser onto the condensate to pump the atoms in stateto a high-field-seeking Zeeman sublevel and eject them from the trap.[46]Next,we set the parameters as ν=0.01,γ=200π,g=100π,and T=0.01.Consequently,if the number of atoms is odd,the transition between the statesandis allowed.Once the system evolves from the Fock statetothe pump laser will evolve the system from(as shown in Fig.2(b)).After this,further transition is forbidden because the number of atoms in the condensate is now even(as shown in Fig.2(c)). Therefore,we can prepare a condensate with an even number of atoms in stateThe procedure to obtain an odd number of atoms is similar. Fig.2. The procedure to obtain an even number of atoms. (a)The atoms are prepared in the internal stateat first. (b)With the resonance condition of the odd-allowed transition fulfilled,one atom is allowed to transition from statetoand then be pumped to an untrapped state.(c)The resonance condition is no longer fulfilled as the number of atoms has changed from odd to even.(d)The evolution of transition probability of the atoms in the Fock states(odd)and(even)with ν=0.01,γ=200π,g=100π,and T=0.01. Precisely controlling the atom number of the BEC remains difficult even with the feedback control technique.[47]Here,we propose a scheme to precisely control the atom number of the condensate using the N-dependent resonance condition.For a condensate with atom number N±a,where a is the atom number uncertainty(here we set N=22 and a=2),we can obtain a condensate of atom number N=20 as follows:Firstly,we prepare all of the atoms in stateand then turn on the pump laser,in the same way as mentioned in the above subsection.As shown in Fig.3(d),the resonance condition is separated when the atom number in stateis different.Furthermore,the separation will increase as n±in the resonance condition(16)increases.Therefore,for example,we can adjust the parameters to ν=0.01,γ=50,g=10,and T=8π/280 to meet the resonance condition ofonly without arousing the transitionand other transitions as well.If there are 24 atoms in statewith the pump laser continuously pumping the atoms in stateout of the condensate,one atom will transition fromtoafter several kicks and then leave the condensate.Next,we adjust the pulse separation T=8π/270,which satisfies the resonance condition ofto pump another atom out of the condensate.Repeating the process,we can also eliminate the possibility ofand get a desired population distributionThus,we could prepare a nonclassical state in the many-body system with fixed atom number,which is important in quantum computing and metrology.[48]It is difficult to measure the atom numbers in stateowing to the indistinguishability of the bosons,but we can confirm it by detecting the atoms in statebecause the atoms would not show up in stateunless the atom numbers in statesatisfied the resonance condition. When the resonance condition is satisfied,the transition speed w can be expressed aswhereObviously,a shorter pulse separation T will lead to a faster transition speed and thus a shorter preparation time.Recalling the unit of time 1/ω0and assuming a typical trap frequency ω0=2π×10 kHz,we only need tens ofµs or even less to realize a transition as shown in Figs.1(b)and 2(d),which is much shorter than the BEC lifetime. Fig.3.The procedure to obtain the desired number of atoms.(a)The atoms are prepared in stateat first.(b)With the resonance condition offulfilled,one atom is allowed to transition from statetoand be pumped to an untrapped state.(c)The further transition is stopped because the population has changed,but we can restart it by altering the parameters to fulfill the resonance condition ofetc.(d)The transition probability after 60 kicks with ν=0.01,γ=50,and g=10. We have calculated the transition dynamics of a two-level BEC system through a perturbation method.From the analytical solution,we found that the transition probability induced by a single weak kick could be ignored.However,when the pulse separation T and the energy differences of the angular momentum eigenstates γ+g(2k±1)fulfilled the resonance condition[γ+g(2k±1)]T=2πn±,the transition probability would quickly add to a considerable value as the kick number increased.It has been found that the resonance can be Nindependent or N-dependent in some special cases.For the Nindependent resonance,the transition has an odd–even sensitivity to the population difference.Based on this,we proposed a scheme to control the atoms in one of the internal states to be odd or even.while for the N-dependent resonance,we proposed a scheme to precisely control the atom numbers.The manipulations of the transitions can be experimentally tested in the existing setups.Adjustment of the pulse separation T could be achieved easily through the acousto-optic modulator.As for the two-body interaction,we can adjust it through the Feshbach resonance.[49] Our findings provide a new route to the manipulation of transition dynamics.The precise control of the atom number could improve the precision of collision shifts and therefore of atomic clocks.[50]Additionally,the preparation of the nonclassical state with certain atom numbers is essential for the sensitivity of two-mode interferometers[51]and the quantum metrology.[48]Furthermore,our study can be extended to the double-well system easily.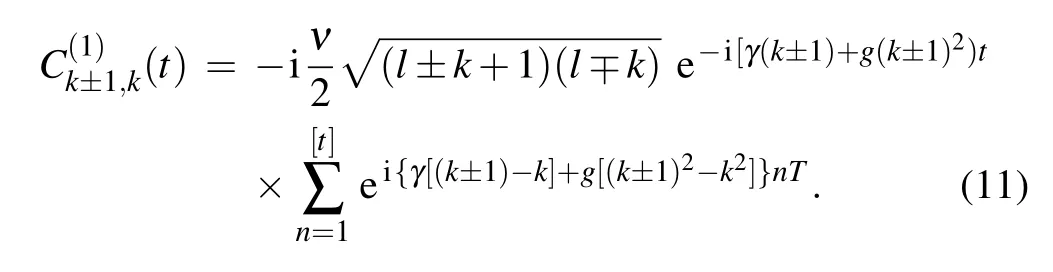
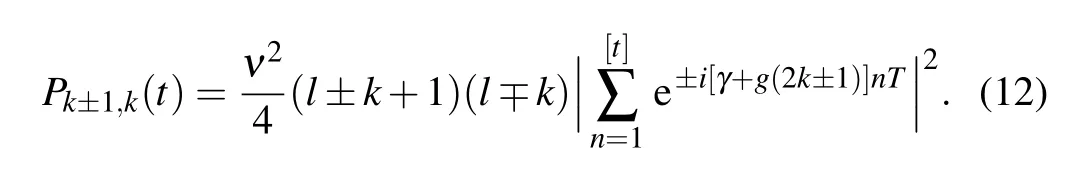


3.Manipulating transition via different resonances

3.1.The N-independent odd–even sensitive transition

3.2.The N-dependent population transform
4.Conclusion
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Compact finite difference schemes for the backward fractional Feynman–Kac equation with fractional substantial derivative*
- Exact solutions of a(2+1)-dimensional extended shallow water wave equation∗
- Lump-type solutions of a generalized Kadomtsev–Petviashvili equation in(3+1)-dimensions∗
- Time evolution of angular momentum coherent state derived by virtue of entangled state representation and a new binomial theorem∗
- Boundary states for entanglement robustness under dephasing and bit flip channels*
- Topological phases of a non-Hermitian coupled SSH ladder*
