知识·策略·创新：解题教学的三重境界

2019-09-04江苏省仪征市新集初级中学211403

中学数学研究(江西) 2019年8期

江苏省仪征市新集初级中学 (211403)

李爱民

“解题”在现代汉语词典中有三层含义，数学中的含义是指解答或演算习题、试题.解题是一种实践性的技能，就好像游泳一样.[1]刚开始是观察和模仿别人，如果被模仿的人能提供有效的帮助，学习者再勤加练习，技能自然能学会学好.在学习解题时，模仿者是学生，被模仿者和提供帮助的人是教师，教师借助解题教学帮助学生学会解题.解题教学不是数学教学的全部，但解题能培养学生的四基四能，锻炼学生克服困难的意志，培养严谨的科学态度，增强应用意识，发展创新能力.更重要的是解题还是考核学生，决定学生升学、未来发展的评价工具.不同的解题教学境界，发挥育人的功能也不一样.

笔者借助教学中的两个问题，谈谈解题教学的境界.

1.解题教学的三重境界

1.1 境界一：授之以鱼，知识境界

问题1如图1，△ABE，△ADC分别是△ABC关于AB，AC边所在直线对称的轴对称图形，若∠1∶∠2∶∠3=7∶2∶1，则∠α的度数为.

图1

本题是在学习“轴对称性质”之后的一道填空题.主要考查轴对称的性质：“成轴对称的两个图形全等”，再由全等的性质可以得到“全等三角形对应角相等”，最后再找到所求的角α与已知角的联系，求出α的度数.

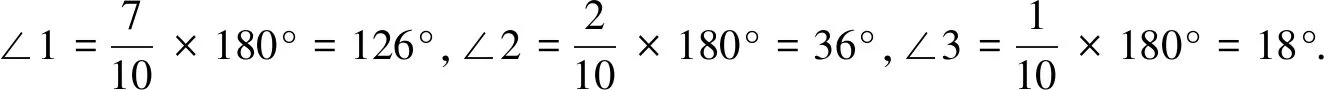
图2

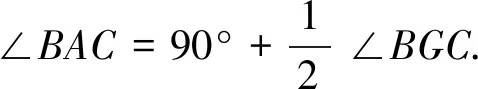
思路3：(利用规形图(或飞镖图)求解)如图3，这是在学习多边形内角的时候总结的一个基本图形，因为它被广泛地运用到求不规则多边形内角和之中，形状像圆规和飞镖，所以被称为规形图或者飞镖图.这个图中的角有这样的一个结论：∠DGE=∠D+∠E+∠DAE.证明这个结论不难，如图4，可以延长线段DG与线段AE相交于点F，借助外角的性质可以证明，具体求解略.

图3 图4 图5

现在回到图1，借助规形图可以得到∠DGE=∠D+∠E+∠DAE，而根据对称的性质可以求出∠D=∠2=36°，∠E=∠3=18°，∠BAE=∠DAC=∠BAC=126°，所以∠DAE=∠BAE+∠DAC+∠BAC-360°=3×126°-360°=18°，因此∠DGE=36°+18°+18°=72°，所以∠α=180°-∠DGE=180°-72°=108°.

思路4：(利用8字形求解)如图5，这是苏科版教材七下“12.2证明”第三课时中的一个例题类似的图形，例题是证明∠G+∠E=∠A+∠C(具体的证明略)，因为形状像数字8，故而起名为8字形.

回到题1，由对称可以得到∠E=∠DCA=∠3，再借助8字形结论就可以得到∠α=∠EAC=∠DAC-∠DAE=126°-18°=108°.

解题教学中首要的任务就是借助解题达到巩固知识、应用知识的目的.要最大限度发挥问题的知识功能，教师必须要精选精讲，切忌就题论题，一题一法，只注重问题的结果，忽略对问题多角度的思考.本题虽然是一道填空题，但它提供了丰富的图形背景和数量关系，所以教师要抓住这个契机，引导学生观察图形，主动参与发现基本的数学模型，提升应用知识的能力，充分挖掘试题的知识价值.

通过问题1的解题教学，学生及时巩固了新知，复习了一些基本数学模型，培养了发散思维，达到了授之以鱼的效果，解题教学境界属于知识境界.

1.2 境界二：授之以渔，策略境界

问题2如图6，在△ABC中，∠ACB=90°，点D、E是AB上的两个点，AC=AD，BE=BC，求∠ECD的大小.

图6

本题是以直角三角形的两个锐角为顶角，在直角三角形内部构造出两个部分叠合在一起的等腰三角形.图形中角之间的关系比较复杂，可以采用整体思想求解，也可以设参数帮助求解，但这两种解题的策略对学生要求较高，成绩中等及以下的学生难以解决.结合条件和结论可以看出这里还存在一个有趣的结论，所以有必要进行适当的变式和延伸，目的是引导学生探索解题的思路，积累解题的经验，获取研究问题的策略，提升思维的宽度和深度.

为了降低问题的难度，变抽象为具体，笔者采取强化条件的改编策略.

变式1 添加∠A=20°，求∠ECD的大小.

为了进一步强化变式1的解题思路，为后续学生发现∠ACB和∠ECD的数量关系做准备，笔者采取异化∠ACB的度数的改编策略.

变式2 在△ABC中，∠ACB=120°，∠A=20°，点D、E是AB上的两个点，AC=AD，BE=BC，求∠ECD的大小.

有了变式1和变式2的解题经验，笔者自然地采用“弱化条件”的改编策略，将∠A=20°的条件去掉，也就出现的原题和变式3.

变式3 将原题中的∠ACB=90°改编为∠ACB=120°.

在完成原题和变式3之后，笔者采用“一般化条件，探索一般性结论”的改编策略，将∠ACB的角度进一步一般化.

变式4 在△ABC中，∠ACB=α，点D、E是AB上的两个点，AC=AD，BE=BC，猜想∠ECD与α有何关系，并验证你的猜想.

解题教学中最重要的任务是为学生提供解题策略的指导.一切解题策略的基本出发点在于“变换”，就是把面临的数学问题，转化为一道或几道易于解答的新题，通过对新题的考查，发现原题的解题思路，最终达到解决原题的目的.[2]本题的条件和问题均不复杂，已知的角度只有∠ACB=90°，要求∠ECD的大小.可见，∠ACB与∠ECD之间隐含着一定的关系.教学中一方面要帮助学生找到解题的方向，另一方面要帮助学生挖掘出问题的本质，体会数学思想方法，培养数学思维.笔者通过将问题条件强化、异化的策略，引导学生理清问题探究的思路；通过将问题条件弱化、一般化的策略，引导学生抓住问题本质，探究出一般性的规律，以达到做一题，会一类，通一片的效果.

通过问题2的解题教学，学生获取了将复杂问题简单化、抽象问题具体化、陌生问题熟悉化、一般问题特殊化等解题经验，培养了分析问题，解决问题的能力，达到了授之以渔的效果，解题教学境界属于策略境界.

1.3 境界三：授之以塘，创新境界

笔者在引导学生探究出问题2一般性的结论之后，为了进一步挖掘问题的内涵，培养学生发现问题、提出问题的能力，笔者引导学生借题发挥，创造出新的问题.

教学片断：

师：通过探究我们发现了∠ACB和∠ECD的一般数量关系，你能借助这个结论重新编制一个问题吗？

生1：在△ABC中，∠DCE=50°，点D、E是AB上的两个点，AC=AD，BE=BC，求∠ACB的大小.

师：把条件和结论互换，是逆向思维的体现，非常好.

生2：在△ABC中，点D、E是AB上的两个点，AC=AD，BE=BC，问△CDE是什么三角形呢？

师：你认为是什么三角形呢？你是如何想的？

师：由对角的关注转化成对三角形形状的关注，改变了考虑问题的视角，很不错.

生3：在△ABC中，∠A=20°，点D、E是AB上的两个点，AC=AD，BE=BC，求∠ECD的大小.

师：你能求出∠ECD的度数吗？

生3：(想了片刻)哦，不能.

师：为什么？

生3：因为知道∠A并不能确定∠ACB的大小.

师：对，一个角是不能确定三角形的形状的.但你想到借助老师一开始的问题，通过弱化条件的方法来改题，活学活用，值得肯定.

生4：当△ABC是等腰直角三角形时，判断△CDE的形状.

师：你知道是什么三角形呢？

生4：(想了一下)顶角是45°的等腰三角形.

生5：当△ABC满足什么条件时，△CDE是等边三角形？

师：不错，改编成了条件探索问题，那你知道满足什么条件呢？大家一起探究一下.

(经过一段时间讨论探究，大部分学生表示△CDE不能是等边三角形，也有几个学生认为可以.)

师：能分别说明一下理由吗？

生6：(认为不能的代表)因为这个时候，△ACB与△CDE都是等边三角形，两个三角形重合了.

生7：(认为能的代表)△ACB与△CDE是重合了，因为∠DCE随着∠ACB的变化而变化，当∠DCE=60°时，∠ACB也等于60°，点D、E分别与点B、A重合，题目条件中说点D、E是线段AB上的两个点，当然包括A、B两点，这是一种特殊情况.

师：(教师肯定了生7的说法，继续追问.)如果∠ACB的度数比60°小，会怎样能？

集体：点D、E会分别到线段AB延长线上和反向延长线上.

师：是两个点都到线段AB的外部了吗？那之前的结论还成立吗？

(在老师的启发下，学生开始画图、探究、小组讨论，经过探究他们发现可能两个点都到了线段AB的外部，也有可能一个在外部一个还在线段AB上，但结论都依旧成立.)

师：现在我们还可以提出什么问题呢？

生8：在△ABC中，点D、E是直线AB上的两个点，AC=AD，BE=BC，猜想∠ECD与∠ACB有何数量关系，并验证你的猜想.

师：刚刚同学们从点动的角度提出问题，那能不能线动呢？

生9：如图7，在△ABC中，∠ACB=90°，点D、E是AB上的两个点，AF=AD，BE=BC，求∠CGF的度数.

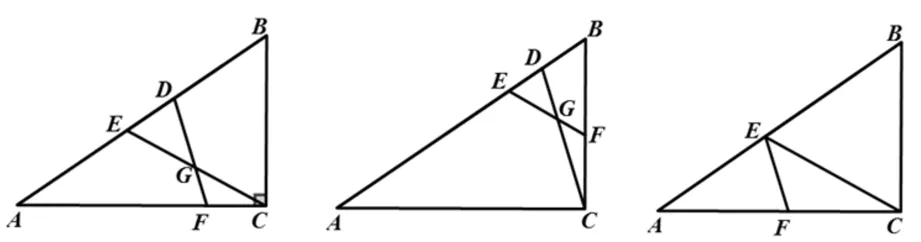
图7 图8 图9

生10：将∠ACB=90°去掉，改成探究∠CGF与∠ACB的数量关系.

生11：如图8，在△ABC中，点D、E是AB上的两个点，AC=AD，BE=BF，探究∠CGF与∠ACB的数量关系.

生12：如图9，在△ABC中，点E是AB上的两个点，AE=AF，BE=BC，探究∠CEF与∠ACB的数量关系.

生13：如图10，在△ABC中，点E是AB上的两个点，AE=AF，BE=BG，探究∠FEG与∠ACB的数量关系.

图10 图11

生14：如图11，在△ABC中，点D、E是AB上的两个点，AD=AG，BE=BF，线段GD、FE的延长线交于点M，探究∠FMG与∠ACB的数量关系.

解题教学中必要的任务是培养学生的创新意识.课程标准(2011)新增的核心概念就是创新意识.课标指出：“创新意识的培养是现代数学教育的基本任务，应体现在数学教与学的过程之中.”[3]解题教学是数学教学的重要组成部分，所以可以借助解题教学培养学生的创新意识.在问题2的基础上，学生能自主的从颠倒条件与结论、从形内到形外、从线段到直线、从点动到线动等不同的视角发现问题、并创造性地以文字、图形、符号语言等形式提出新的问题.学生提出的问题优劣暂且不论，但是学生从中获得了成功体验，激发了学习兴趣，培养了创新意识.

通过问题2的解题教学，培养了学生发现问题、提出问题的能力，达到了受之以塘的效果，解题教学境界属于创新境界.

2.三种境界间的关系

2.1 递进关系

从知识境界到策略境界，再到创新境界，解题教学境界的层次逐渐提升，呈现出递进的关系.解题境界的高低取决于教学理念定位的高低.教学理念是获取知识，解题教学就只会关注问题“怎样解”；教学理念是培养学生的能力，解题教学还会关注“为什么这样解”“怎样学会解”；教学理念是立足学生未来发展，培养学生的数学素养，解题教学就还会关注“还能解什么”.