广东省广州市第一一三中学(510000)余瑜

思维总是从问题提出开始的,进而在师生之间双向互动的有效沟通和深度交流的碰撞发展的.在以问题为导向的课堂教学中,一个好的问题往往能激发学生的学习兴趣,提升思维能力.基于此,有效的课堂提问至关重要,会“提问”,善于“提问”,才能让学生实现思维超越.以下结合教学实践,从思维的逻辑性、发散性和开放性三个着力点,探析课堂提问的有效方法和策略.

一、提问具备逻辑性是提升思维的着力点

思维逻辑能力反映在学生的科学探究能力和逻辑推理能力上,而学生数学解题逻辑的生成,有赖于问题探究和不断追问的刺激.题1 是人教版教材中的例题,如何设计小问题探究,配合有效的提问,以建立与例题解题思维的关联呢?

题1 如图1,点P为等边△ABC内一点,且PA= 2,PB=求∠BPC的度数.

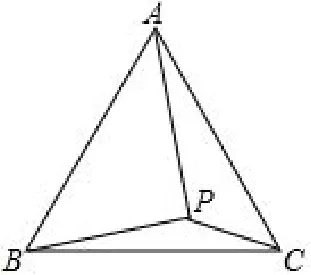
图1

对于题1,已知边长求角度,学生会觉得梯度太高,没有抓手,所以引导学生通过观察边长的特殊性,从而构造特殊三角形解决问题是关键.

因此,可设计两个小问题设计,让学生独立思考和探究后,教师再进行有效追问.

问题1(1)已知,在△ABC中,AB=AC=BC=2,则∠B=____.

(2)已知,在△ABC中,AB= 2,AC== 1,则∠B=____.

问题2如图2,已知等边△ABC与等边△BDE有公共顶点B,(1)请你找出图中的全等三角形;(2)若AE=BE= 2,CE= 1,则∠DAE=____;∠BEC=____.

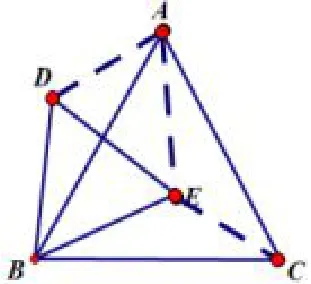
图2

追问过程呈现如下:

追问1:根据问题1 的解法,我们是如何求出角度的?

生1:根据特殊三角形求角度.(经验1)

追问2:你发现例题所求线段与问题1 所求线段的区别和联系吗? (观察、感知、类比)

生2:例题相当于是把问题1 的线段分散在一个等边三角形的内部.

追问3:观察问题2,思考你发现的全等三角形的作用是什么?

生3:将线段EC转移到线段AC的位置.(观察、分析)

追问4:例题中的三条分散的线段如何进行“等量转换”?

生4:利用相等或全等.(类比推理)

追问5:等量转换的途径有哪些? 应该选择哪一个呢?依据是什么?

生5:全等、平移、轴对称、旋转(经验2).因为AB=AC,所以应该选择旋转(转化思想).即以点B为中心,将△BPC逆时针旋转60 度.(知识应用)

追问6:旋转角度如何确定?

生6:要使旋转后的边AB与边AC重合.(旋转应用)

追问7:可以以点P为中心吗?

生7:不可以,因为没有以点P为顶点的等线段.(辨析思维)

通过层层追问,使本题的解题逻辑逐渐浮出水面:

分散线段⇒集中(特殊三角形)⇒利用相等⇒全等、平移、轴对称、旋转⇒有共顶点的等线段⇒旋转

上述追问让学生在逻辑思维和数学语言训练的同时,产生新旧知识的碰撞,获得解题思路.这个问题的解决本身有一定的深度和广度,当学生直面问题时,需要将思维断点和盲点显性化,通过递进式的问题,引导学生层层突破,延伸学生的数学思维,指导学生抓住问题的本质,逐个击破,并达到解决问题的目的.在这样的提问方式下,学生经过不断思考,思维碰撞,能够对教师所提出的问题进行深刻的分析和理解,通过一个个小问题的突破,最终破解整体的大问题.

其实,问题的设计不是一蹴而就的,笔者原先有一设计,问题1 不变,而把问题2 设计为:已知线段AB,请你将点B绕点A逆时针分别旋转30°后得到点C,连接对应点并观察所得到的图形是什么特殊三角形? 若旋转角分别为60°,90°,这又是怎样? 而问题3 设计为:请作出任意一个△ABC绕顶点B逆时针旋转60°后得到的图形,连接对应点,你有什么发现?

在这个设计中,意图使学生经历通过旋转产生特殊图形进而解决角度问题,但是在实际的教学过程中发现学生没办法依托问题串的解答,进而类比完成题1 的学习,究其原因,就是在设计问题的时候没有按照学生的思维逻辑来设计,问题串之间的关联性不强,学生无法整合理解.

二、提问具备发散性是创新思维的着力点

关注学生思维的发散点,就是在提问过程中将一个问题从多角度、多层次、多方位设问,引导学生沿着不同方向思考,探求不同解题方法,以培养学生数学思维的深度和广度以及创新能力.有些题目简单,但鼓励学生一题多解,给学生充分的时间进行思考和探究,他们的答案会让教师惊喜.发散思维常常藏在简单题中,教师勿因简单而放弃思考和提问.

题2如图3,已知△ABC,回答问题:

(1)写出△ABC各顶点的坐标;

(2)求△ABC的面积.

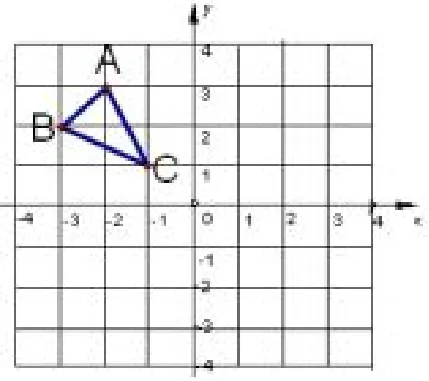
图3

分析问题的重难点在于求△ABC的面积,面积的求法有很多种,不局限于某一解法才能打开学生的思维,所以在处理本题时提问着力于鼓励学生一题多解.

提问你能用多少种方法来求出这个三角形的面积问题呢? 我猜大家都不止一种,请你画出图形并说出你的做法吧.

学生1 想到补成矩形;学生2 想到补成梯形;学生3 想到补成三角形;学生4 的方法是先补成四边形,再将四边形割成梯形和三角形来计算,最后减去一个三角形面积即可;学生5 想到了将三角形沿着平行于坐标轴的直线切割的方法来求,学生6 的方法更巧妙:如图4,利用平行线、等积法转化三角形面积;学生7 的方法是利用中心对称将三角形面积转化为等腰直角三角形和正方形的面积和,如图5.

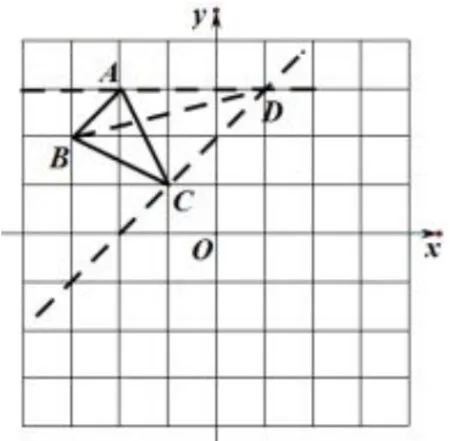
图4

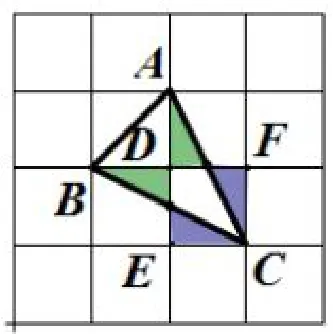
图5

让学生发散性的积极思考、去探索、去讨论,在这些过程中学生的思维得到锻炼,主体地位得以充分体现.笔者在备课时完全没有预设学生所用的方法6 和方法7,因为初一的学生并不太熟悉等底等高和旋转对称,他们无法规范书写这些解法,但是其中的数学思维却是很好的,这样,学生在学习过程中不断对这些解题方法进行推敲、对比,最终筛选出最便捷、最高效、最适合自己的解题思路,从而形成科学的思维方式.基于此,笔者发现,在思维延展处类比提问能促进学生思考,举个简单例子,如题3 的解决思路的获得.

题3(课本原题改编):用一条长40m 的篱笆,怎样围成一个面积为75m2的矩形菜园? 能围成一个面积为101m2的矩形菜园吗? 如能,说明围法,如不能,请说明理由.

学生对于这一类型的题目已经比较熟悉,解题思路也比较清晰,笔者在这个基础上追加三个问题给学生思考:

追问1:如图6,利用一边足够长的墙,围成一个面积为150m2的矩形菜园,矩形的边BC为多少?

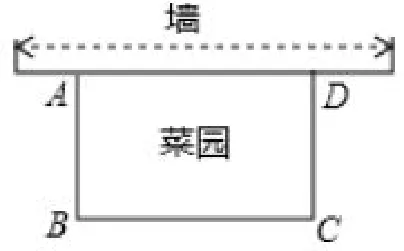
图6

追问2:求矩形的边BC为多少时,菜园的面积最大?

追问3:若墙长为15m,则矩形的边BC为多少时,菜园的面积最大?

通过改变题设的个别条件,使学生引发新的思考和分析,且新的问题需要串联其他单元知识来解决,从而使学生的解题思维更加严谨、系统.魏书生说:“知识是‘生长’出来的”,创新思维亦是如此获得.

三、提问具备开放性是创造思维的着力点

爱因斯坦提出:“提出一个新的问题,新的可能性,从新的角度去看旧的问题,却需要有创造性的想象力,而且标志着科学的真正进步.”学生学习最好的途径是自己去发现问题,自己去解决问题,如在学习菱形的判定时,一般的学习方式是由教师引导学生复习菱形的定义和性质,然后从菱形的边、角、对角线进行探究,通过“观察——归纳——猜想——验证”进行学习,这种单向式引导能保证组织数学活动的有序推进和有效实施,但要实现建构数学的意义和理解,需要教师在教学过程中不断调整自己在活动中的角色,让学生在互动交流中进行深层次的学习.由此,笔者对这节课的设计做了适当变化,采取开放式提问方式引导学生进行探究:

师:今天在我们学习新知识之前,请同学们根据自己的理解画出菱形,或利用长方形纸片折或画出一个菱形,并且跟同伴交流你的菱形是怎么得出来的.

生1:先画2 条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,得到一个菱形.

生2:我画出两条互相垂直平分的线段,再将他们的端点首尾相接得到菱形.

生3:我先做出一个矩形,再分别取矩形的四边中点,连接形成菱形.

生4:我先做出一个等腰三角形,再将它沿底边对称,得到菱形(或者画两个全等且有公共底边的等腰三角形).

生5:将一张长方形的纸横对折,再竖对折,然后沿图中的虚线剪下,打开即可.

生6:两张等宽的纸条交叉重叠在一起,重叠的部分就是菱形.

生7:将一张长方形纸对折,再在折痕上取任意长为底边,剪一个等腰三角形,然后打开即是菱形.

师:非常棒! 接下来请大家挑选一种画法,证明这种画法得到菱形的结论成立或不成立,并与同伴分享你的结论.

新的设计通过让学生自主地画出一个菱形,不仅使学生主动思考“何为菱形”、“菱形有什么性质”,更激发学生深层次地思考“为什么我所画出来的图形是菱形”,从而建构出菱形的判定定理,教师在这一过程中根据学生的不同回答需要做出不同的引导,对于一些不在预设的学生答案也要给予鼓励和有效指导.可见,开放性问题以体现对学生创新意识的培养,避免单一的传授知识的互动阻碍学生思维灵活性的发展.而聚焦式的互动促进了学生投入到解决高认知要求的数学任务中,让学生有足够的话语权,让学生有更多的提出问题的机会.

四、结束语

我们知道,课堂提问是课堂教学活动中经常使用的教学手段之一,是引发教师与学生之间双边互动交流的活动.教师在提问时,结合教学目标要求和学生的学习实际,科学地设计课堂提问,及时唤起学生有意注意,并活化提问的形式,能使教师的主导作用和学生的主体作用在提问过程中得到展示,思维实现教学相长.