许 晶 ，李世尧 ,2，王斌泰 ，李 静 ,3，蒋秀根

（1.中国农业大学水利与土木工程学院，北京 100083；2.杭州电子科技大学通信工程学院，浙江 杭州 310018；3.河南职业技术学院环境艺术工程系，河南 郑州 450046）

深梁指跨高比较小的梁.深梁是常存在于筏板基础、深基坑支护结构、高层建筑中的转换梁、框筒结构中的梁，基于结构安全和经济角度考虑，提出一种对此类构件的受力性能进行精确且高效分析的计算方法很有必要.

分析梁的两个常用基本理论为Euler-Bernoulli梁理论和Timoshenko 梁理论.基于Euler-Bernoulli梁理论，很多学者[1-4]对梁构件进行了受力分析并提出了各类模型，但是这些研究中均未考虑梁的剪切变形.文献[5-6]研究发现，计算深梁内力时不考虑剪切变形影响会导致结构或构件内力计算结果偏低，故基于Euler-Bernoulli 梁理论提出的计算模型不能对深梁受力性能进行精确分析.

针对深梁，各国学者提出了多种理论，其中Timoshenko[7]于1921年提出的两广义位移梁理论得到广泛应用.该理论认为变形前垂直于直梁中心线的截面在变形后仍保持为平面，但不再假定它一定垂直变形后的中心线，即变形后截面转角与梁轴线转角不再相等，两者之差为剪切角.基于Timoshenko梁理论，一些学者采用静力法和能量法对梁进行了研究，但这些理论方法可精确解决受力简单梁内力和位移的计算问题，对于存在移动荷载和多种荷载共同作用的复杂结构或构件分析，静力法和能量法无法得到满意解.利用深梁理论构造单元时，最为关键的问题是确定剪切修正系数.剪切修正系数有多种计算理论和方法[8-10]，但这些系数是对不同截面的剪应力分布或梁的本构关系采用不同假定得出的，这些假定对简单截面计算结果相同，对复杂截面计算的剪切修正系数不同.

数值计算法中的有限元法[11]以效率更高、适用性更广、精度可以满足工程要求被很多学者用于梁构件受力性能分析中.实际分析中，常采用插值形函数法构造的梁单元对梁受力及变形进行分析.基于Timoshenko 梁理论，不同学者利用线性插值、二次插值、多次插值等方法构造了深梁单元[11-12]，由于这些插值函数为位移的近似方程，计算结构存在截断误差，计算精度较低.为取得较好计算精度，须采取多单元，加密节点的技术，则必然造成计算效率的降低.文献[13-16]考虑剪切变形对沿杆长方向的内力和位移影响，提出了构建杆件单元解析形函数的一般理论，并构造出一系列解析型单元，通过与插值形函数构造的单元对比发现，该解析型单元的计算精度更好，效率更高.

本文以深梁为研究对象，以Timoshenko 梁理论和有限元法为基础，利用Timshenko 梁基本方程建立了深梁位移控制方程，进而构建了梁挠度、截面弯曲转角和剪切角的解析位移形函数.基于势能原理和解析位移形函数，构造了解析型深梁单元.通过计算悬臂梁、简支梁的端部挠度和转角，将本单元与理论解、插值形函数计算的结果进行对比，验证了本解析型单元的高精度、高效性.

1 参数及控制方程

1.1 位移内力参数

如图1所示，深梁总长度为l，梁上荷载有：节点A、B 两端分别受弯矩MA、MB；剪力VA、VB；梁上集中力矩Mi、分布弯矩mi、 横向集中荷载Pi、均布荷载qy，其中，i为横向坐标点.梁上位移有：挠度v；梁两端轴线转角 φA、 φB.所有荷载和位移（挠度、转角）与坐标轴方向一致为正；当截面法线与坐标方向一致时，深梁内力与坐标方向一致时为正，反之为负.

如图2所示，深梁的位移变量有：v；弯曲挠度vM；剪切挠度vV；截面弯曲转角θ；截面剪切角 γ；梁轴线转角 φ.

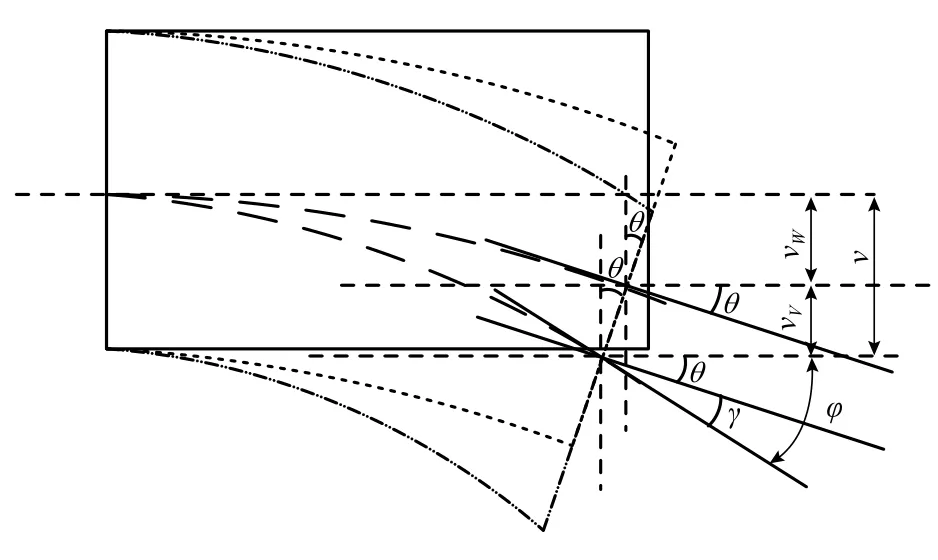
图2 梁微段变形图Fig.2 Deformation of beam micro segment

梁单元的自由度：节点A、B 共有4 个自由度，节点位移向量其中，vA、vB为梁节点A、B 的挠度，θA、 θB为梁节点A、B 的截面转角；单元的节点力向量

1.2 基本方程

1.2.1 几何方程

梁轴线转角方程为

转角关系方程为

截面曲率方程为

1.2.2 平衡方程

力矩平衡方程为

式中：M（x）、V（x）表示沿深梁杆长任意截面的弯矩、剪力.

剪力平衡方程为

1.2.3 物理方程

弯曲刚度方程为

式中：E为材料弹性模量；I为深梁截面惯性矩.

剪切刚度方程为

式中：G为材料剪切模量；A为截面面积；k为截面不均匀剪切系数[17]，，S为面积矩，b为截面宽度.

1.3 位移控制方程

1.3.1 挠度控制方程

由式（4）～（6），可得

由式（1）～（3）和式（7）可得

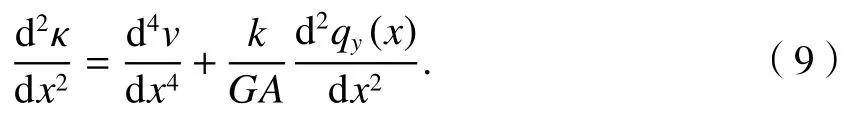
联立式（8）、（9）可得挠度控制方程为

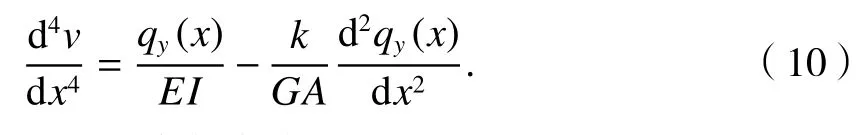
1.3.2 剪切角控制方程

由式（4）、（5）和式（7）可得剪切角控制方程为

1.4 位移协调方程

由式（1）～（7）可得挠度与剪切角的协调方程为

2 单元位移方程

2.1 控制方程求解

2.1.1 挠度控制方程求解

为了建立深梁单元的挠度形函数，不考虑梁上的分布荷载，挠度微分控制方程（10）简化为齐次方程，对其求解，可得挠度为

式中：f为挠度基函数向量，为位移系数.

2.1.2 剪切角控制方程求解

为了建立深梁单元的剪切角形函数，不考虑梁上的分布荷载，剪切角微分控制方程（11）简化为齐次方程，对其求解，可得剪切角为

式中：c5为位移系数.

2.2 位移协调条件的应用

将挠度方程（13）、剪切角方程（14）代入协调方程式（12），可得，剪切角可变为

式中：g为剪切角基函数向量[18]，

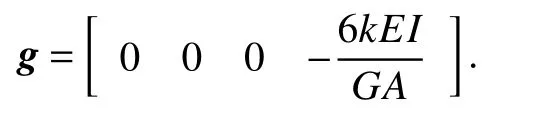
由轴线转角方程（1）、转角关系方程（2）和挠度方程（13），截面弯曲转角可表示为

式中：h为截面转角基函数向量[18]，

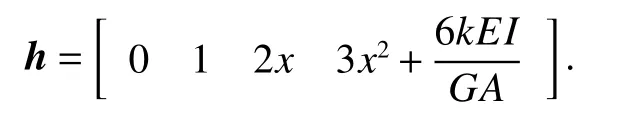
3 单元位移形函数

3.1 位移系数定解

由挠度方程（13）和截面转角方程（16）及节点位移向量表达式，有

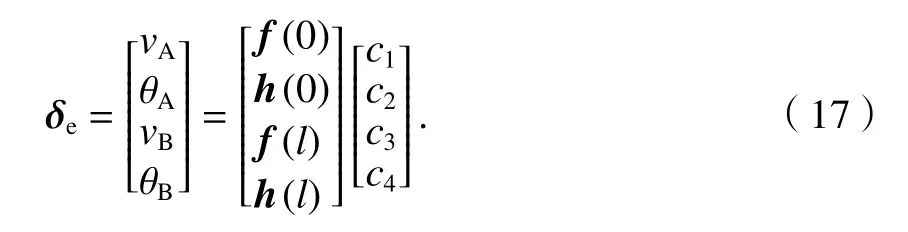
则式（17）用矩阵形式可表示为

位移系数可表达为

则有

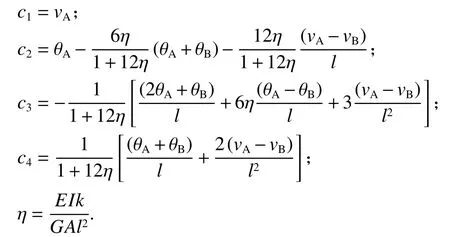
显然，当不考虑剪切变形时，深梁直接退化为浅梁，剪切刚度GA取为无穷大，则η 取为0.

3.2 单元位移形函数

3.2.1 挠度v位移形函数

由式（13）、（19），可得

由位移形函数的定义v(x)=Nvδe，可得

3.2.2 截面转角θ 位移形函数

由式（16）、（19）可得

由位移形函数的定义θ (x)=Nθδe，可得

3.2.3 剪切角 γ位移形函数

由式（15）、（19）可得

由位移形函数的定义 γ=Nγδe，可得

4 Timoshenko 梁单元列式

4.1 单元势能

4.1.1 变形能

单元的变形能为杆件弯曲变形能UM和剪切变形能UV之和，其表达式用位移形函数形式表示为

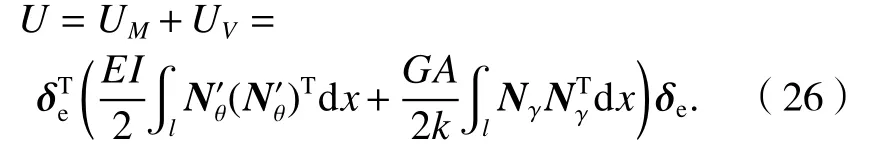
4.1.2 荷载势能

梁的荷载势能由节点力势能、梁上竖向均布荷载势能、竖向集中力及力矩势能组成，其表达式用位移形函数形式表示为

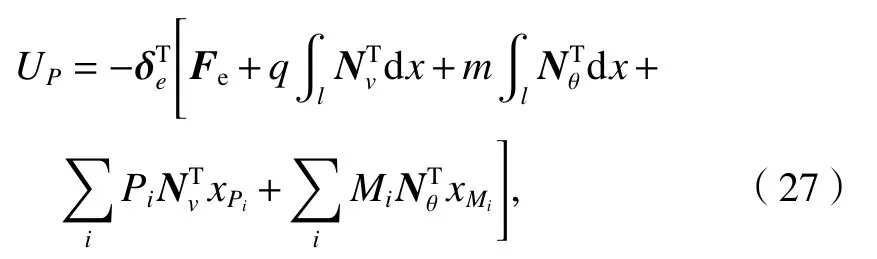
式中：xPi为 横向集中荷载Pi的 作用点位置；xMi为为集中力矩Mi的作用点位置.

4.1.3 总势能

单元总势能为

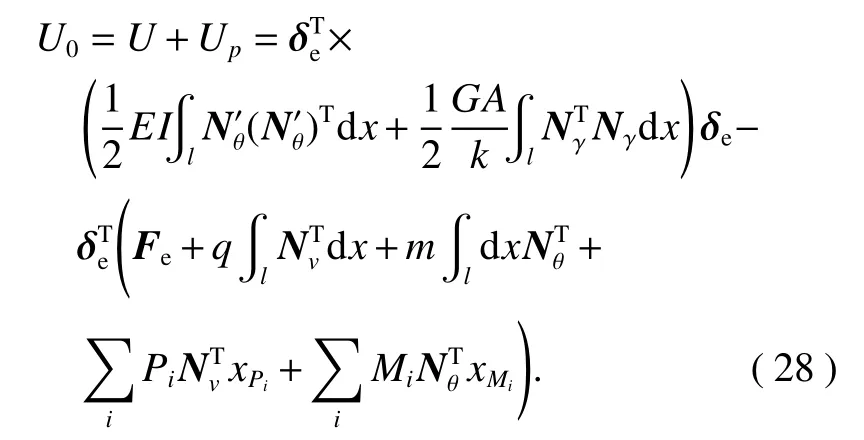
4.2 单元列式

根据势能变分原理，真实的结构位移必然使得单元的势能最小，即对深梁单元，真实的节点位移必然满足由式（28）可得

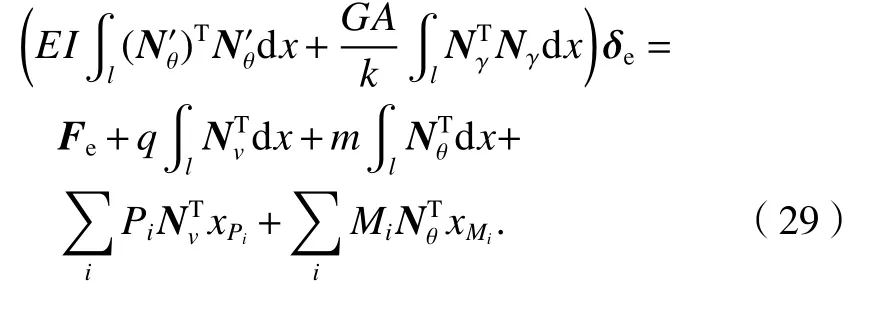
式（29）可简写为

式中：Ke为 单元总刚度矩阵，Ke=KM+KV，KM为弯曲刚度矩阵，其表达式见文献[18]，KV为剪切刚度矩阵，其表达式见文献[18]；为等效荷载向量.

4.3 等效节点力

梁上均布荷载等效节点力向量为

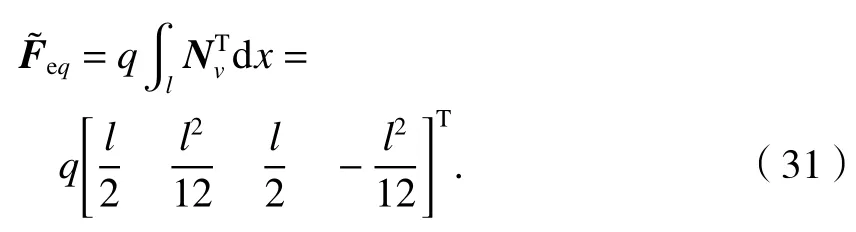
梁上分布力矩等效节点力向量为

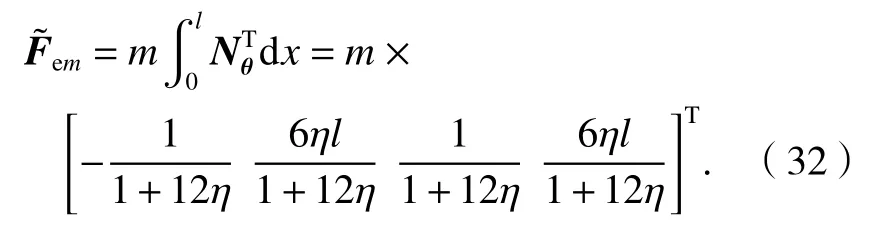
梁上集中力等效节点力向量为

梁上集中力矩等效节点力向量为

4.4 关于适用性的讨论

由KM和KV表达式可得考虑剪切变形影响的单元总刚度矩阵，具体表达式为

不考虑梁的剪切应变，剪切刚度GA取为无穷大，则η 取为0，式（35）可变为

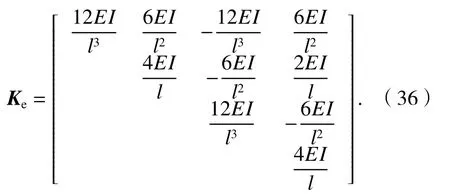
式（36）同Euler 梁单元刚度矩阵一致[16]，由此可见，本文构造的单元总刚度矩阵可退化为Euler梁单元刚度矩阵，且不存在剪切闭锁问题.

5 算例与对比

为验证基于Timoshenko 梁理论，采用解析形函数法构造的梁单元的精确性，分别采用理论解、插值形函数法、解析形函数法求解悬臂深梁和简支深梁的端部位移，并进行对比；为验证剪切变形对深梁位移影响，将Euler 梁单元与Timoshenko 梁单元计算结果进行对比.

5.1 杆件参数

图3为悬臂梁和简支梁受力简图.假定两种梁的截面尺寸均为2 m × 3 m，梁长均为9 m，材料弹性模量E=210 GPa，剪切模量G= 80 GPa，不均匀剪切系数k= 2/3.悬臂梁和简支梁所受的荷载工况：（1）右端集中力100 kN；（2）左端和右端集中弯矩500 kN·m；（3）满跨均布荷载40 kN/m2.

图3 梁构件Fig.3 Beam

5.2 结果与分析

不划分单元，采用解析形函数法计算悬臂梁和简支梁端部位移，并与理论解、插值形函数法的计算结果进行对比，采用Euler梁单元和Timoshenko 梁单元计算的悬臂梁和简支梁结果对比见表1、2.对于悬臂梁，左端为固定端，故左端挠度 νA和 转角 θA为0；对于简支梁，两端为简支，故两端挠度 νA和 νB均为0.

由表1、2 可知，在单元数量相同时，采用解析形函数法构造的梁单元在计算挠度和转角精度上高于插值形函数法构造的单元，这是由于本文构造的解析型单元基于解析位移形函数模式，很大程度消除了模型误差带来的影响.同时，该解析型单元不需要划分单元，即可得到与理论解一致的计算结果.

对于悬臂梁，承受均布荷载作用时，基于Euler梁计算的位移与基于Timoshenko 梁理论构造的解析型单元计算的梁端位移偏差可达到50.000%；承受右端集中弯矩作用时，计算的位移偏差较小.对于简支梁，承受均布荷载作用时，基于Euler 梁计算的位移与基于Timoshenko 梁理论构造的解析型单元计算的梁端位移偏差为0.001%；承受端部集中弯矩作用时，计算的位移偏差可达到10.769%.

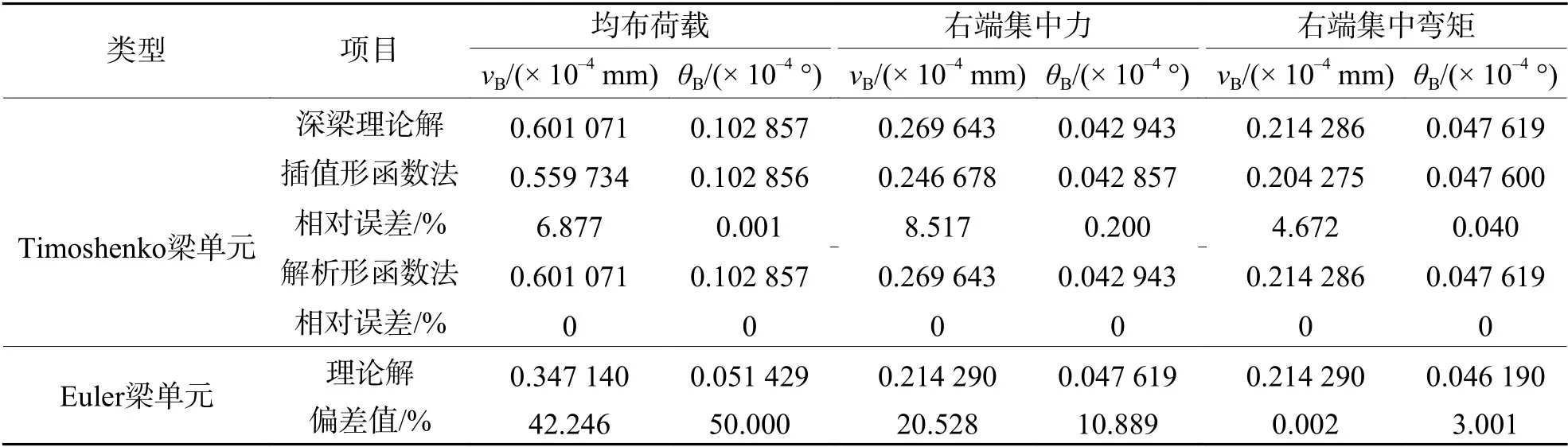
表1 悬臂梁端部位移计算结果对比Tab.1 Comparisons of end displacement for cantilever beam

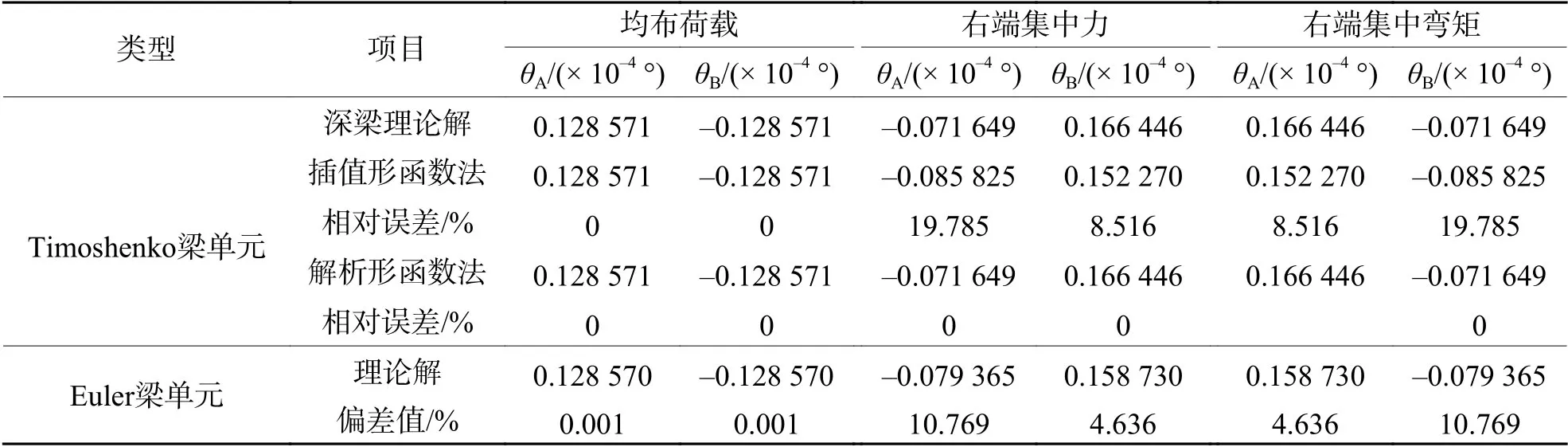
表2 简支梁端部转角计算结果对比Tab.2 Comparisons of end bending angle for simply supported beam

6 结 论

基于Timoshenko 梁基本方程，建立了深梁位移控制方程，构造了深梁单元弯曲挠度、截面转角和剪切角的解析位移形函数；利用势能变分原理，结合解析位移形函数，构造了解析型深梁单元，并给出了解析型深梁单元总刚度矩阵；由势能泛函变分，得到均布荷载、集中力、分布力矩、集中力矩等荷载下的等效节点力.结合单元位移形函数，可得各种复杂荷载下深梁的节点位移.本文构造的解析型单元计算深梁挠度和转角的精度远高于插值形函数单元，且采用一个单元即可保证计算结果与理论解一致，满足了高精度、高效率的要求；构造的深梁单元可用于Euler 梁结构分析，且不存在剪切闭锁问题.