韩朝晖

（湖南文理学院，湖南 常德 415000）

0 引言

随着新材料的不断涌现，有许多材料受拉和受压时变形模量相差较大，在不同应力状态下需要考虑其不同的本构关系，成为了当前研究热点，吸引了广大学者注意力。Medri G建立了考虑受拉受压不同变形模量各向同性材料的非线性模型[1]、Bert CW等[2]、Srinivasan RS[3]研究了受拉受压不同变形模量材料板的振动；李战莉等[4]、曾纪杰[5]、蔡来生等[6]建立了受拉受压不同变形模量材料的本构关系；吴晓等[7]考虑材料的双模量特性，分析了双模量圆板的弯曲变形；罗战友等[8]建立了不同拉压模量及软化特性材料的柱形孔扩张问题的统一解；Ambartsumyan SA[9]、高潮等[10]和吴晓等[11-12]对不同拉压模量板、梁[13-14]的弹性理论解开展了研究；吴晓等[15]和韩朝晖等[16-18]考虑剪切效应建立了不同拉压模量材料的弹性理论。本文考虑双模量材料特性，利用奇异函数对分布载荷作用下不同拉压模量梁的平面应力问题进行了研究，

并推导出了双模量简支梁应力公式的级数解。

1 应力函数

如图1所示双模量简支梁。

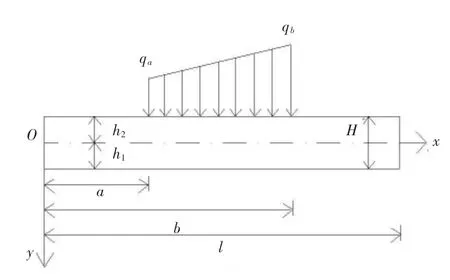
图1 双模量简支梁

其拉伸区和压缩区的应力函数应满足协调方程：

式中：i=1时代表拉伸区，i=2时代表压缩区。以下类同。令式（1）的解为

将式（2）代入式（1）可得

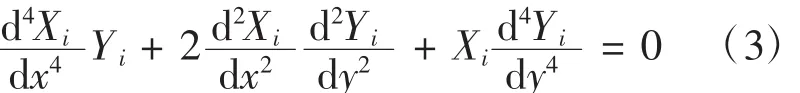
由式（3）可得

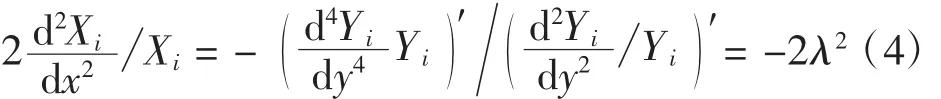
由式（4）可以求得：

将式（6）代入式（3）可得

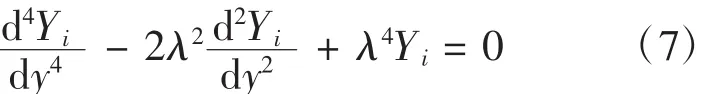
由式（7）可以求得

所以，双模量简支梁的应力函数为

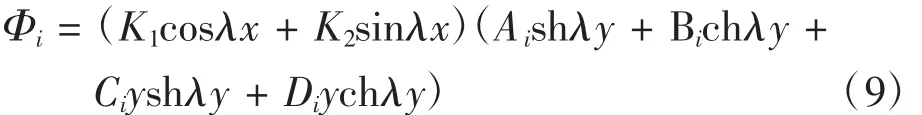
对于图1所示双模量简支梁，在梁两端x=0和x=l时，有

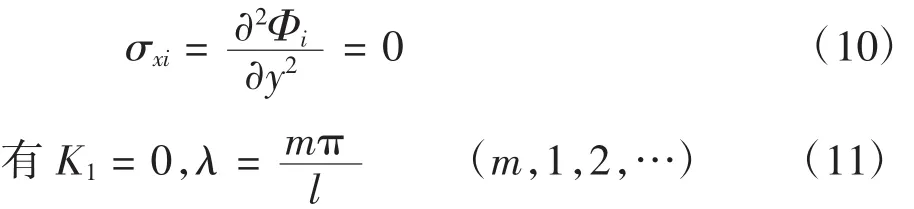
故图1所示双模量简支梁应力函数通解为

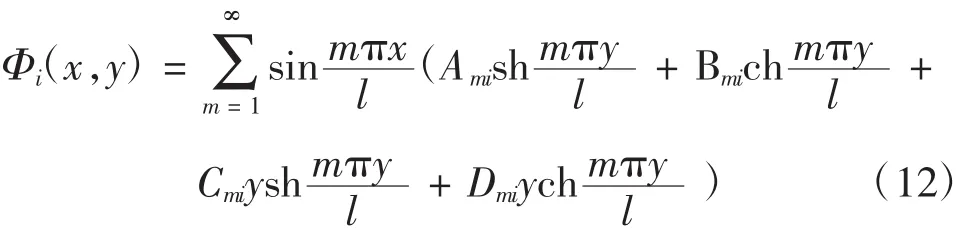
2 应力公式

对于图1所示工程中常见的线性分布载荷可用奇异函数表示为如下形式：

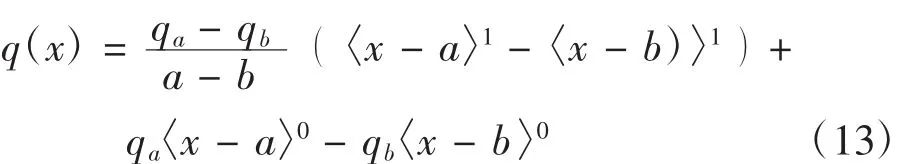
其中，奇异函数运算规则为

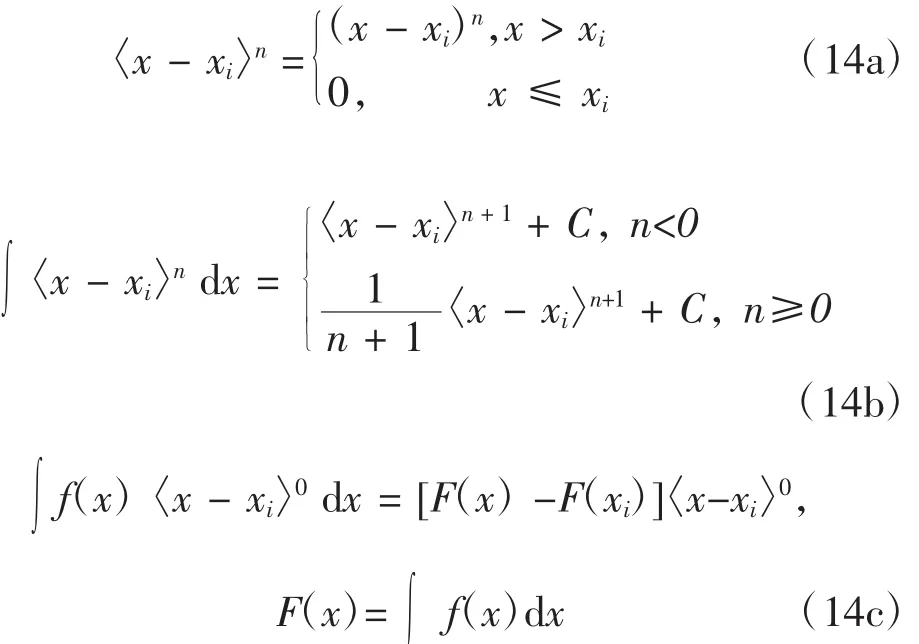
利用傅里叶级数可把式（13）展开为如下形式：

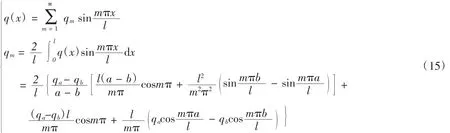
由式（12）可知双模量简支梁拉伸区和压缩区的应力分别为：

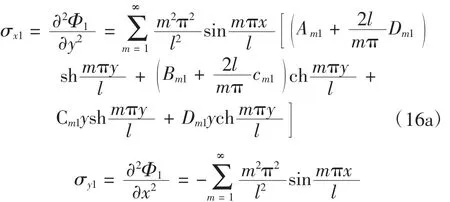
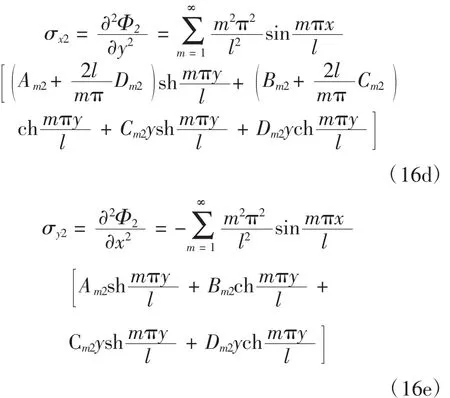
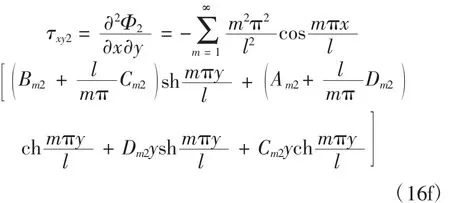
双模量简支梁的边界条件及中性层连续条件分别为

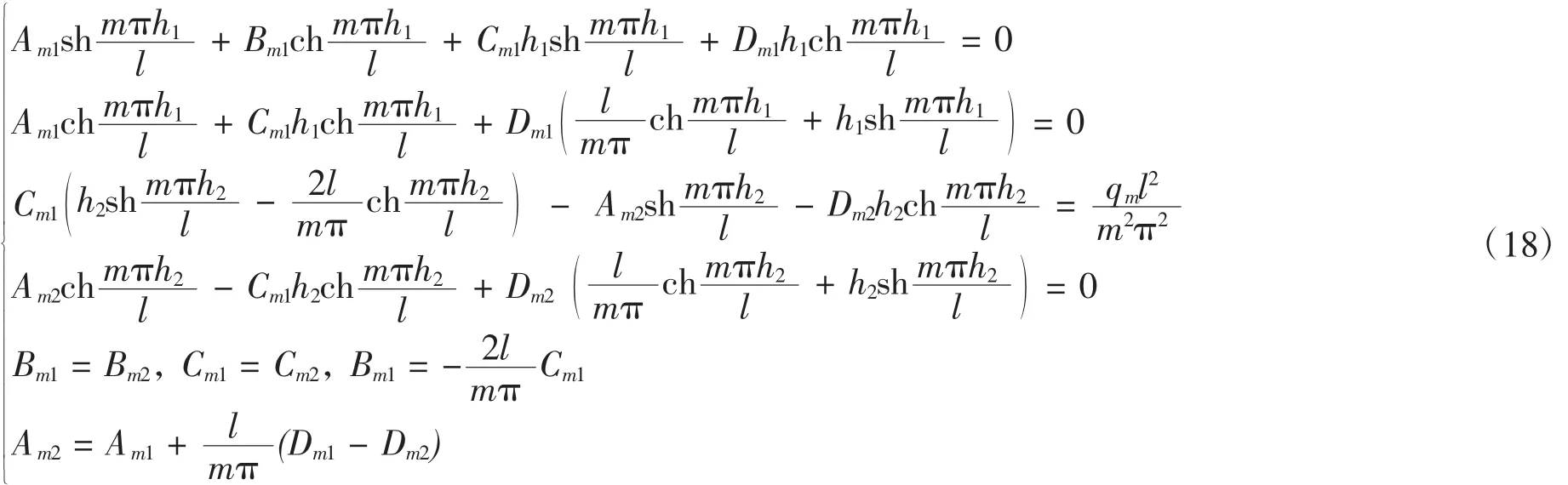
将（16）代入式（17）可得

利用式（18）可以求得

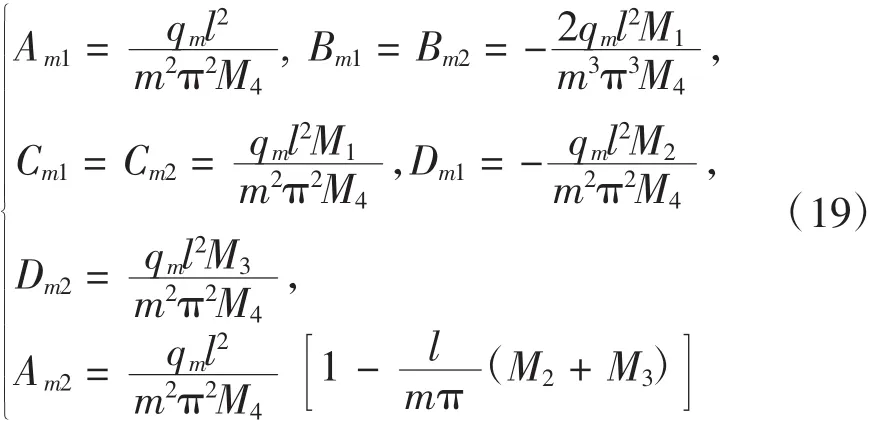
式中：

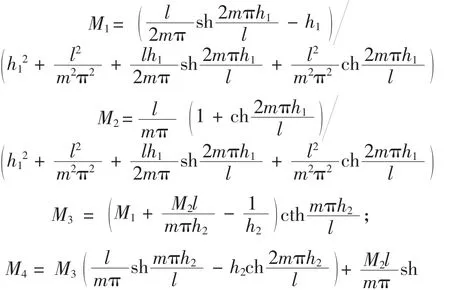
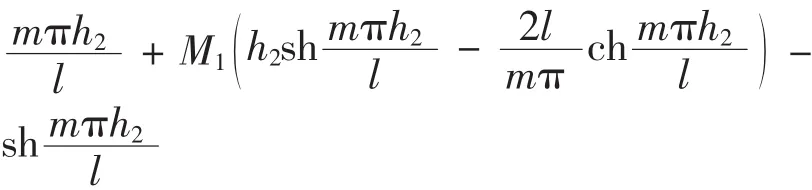
将式（19）代入式（16）即可得到双模量简支梁在横向分布载荷作用下的应力表达式。

3 中性轴位置的确定

双模量梁在外荷载作用下弯曲时的应力和应变关系为

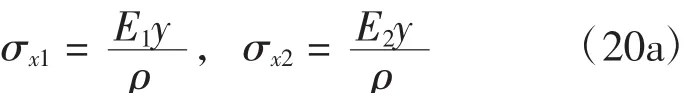
式中：E1为拉伸区的弹性模量；E2为压缩区的弹性模量。

如图2所示任意荷载作用下的简支梁，对B点的力矩平衡方程为

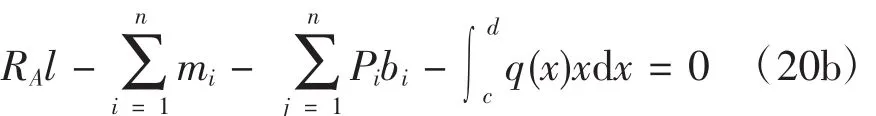
所以，

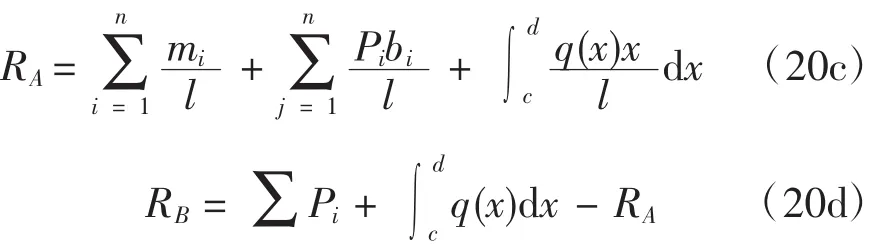
图2 任意荷载作用下简支梁

这样，由简支梁的支座反力，就可以得到各个截面的弯矩表达式。

弯曲时双模量梁的力矢和力矩平衡方程分别为：

将式（20）代入（21）中，可得

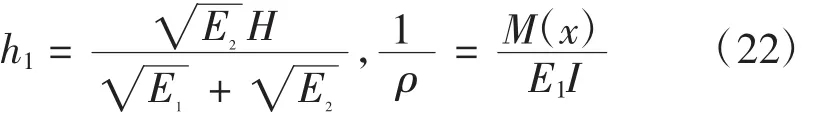
式中：h1为拉伸区高度；h2为压缩区高度；H=

由式（22）可知，双模量梁中性轴的位置与作用在梁的横向载荷无关。

4 算例分析与讨论

设某双模量简支梁的b=1，E1=93.2 GPa，E2=124.36 GPa。采用本文方法计算中点处的最大拉应力及最大压应力，如表1~表4所示。

为验证本文方法，采用ANSYS有限元程序对双模量简支梁中点处的最大拉应力及最大压应力也进行了计算，结果一并列入表1~表4。

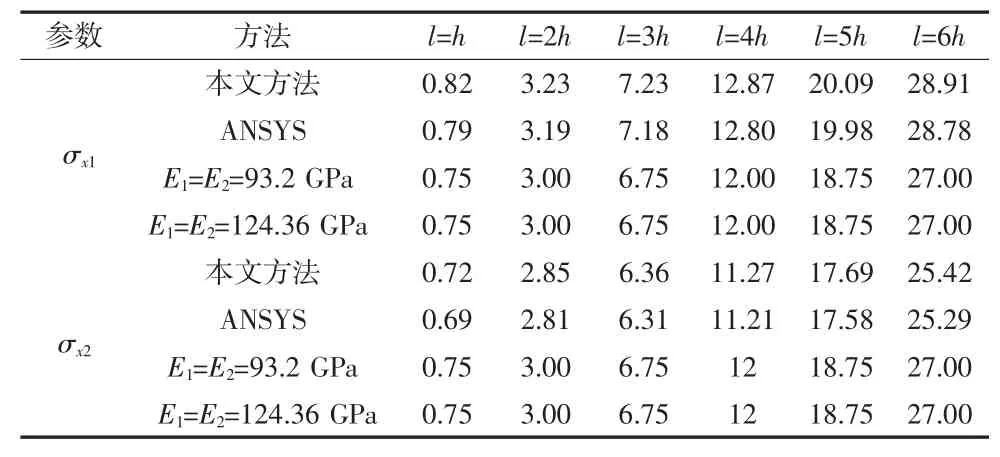
表1 qa=qb，a=0，b=l时双模量简支梁中点处弯曲应力

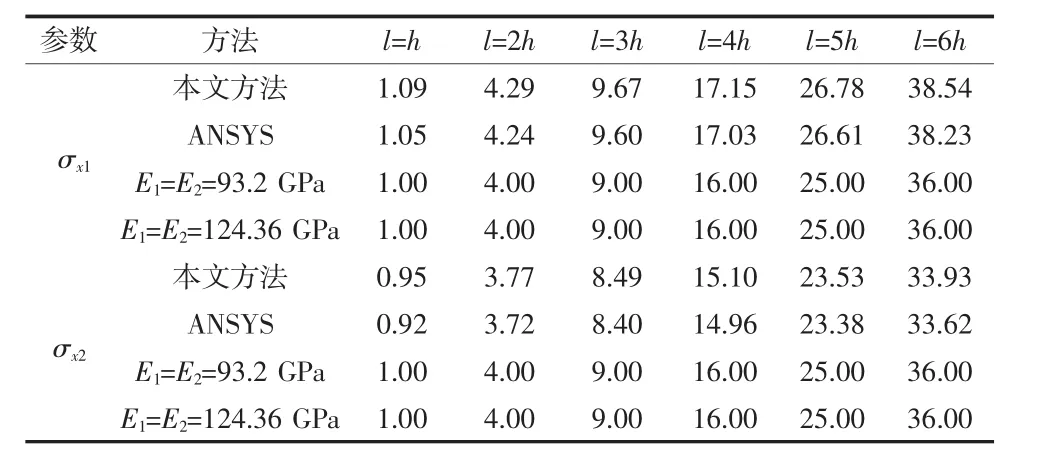
表2 qb=2qa，a=0，b=l时双模量简支梁中点处弯曲应力

表 3 qa=qb，a=，b=l时双模量简支梁中点处弯曲应力

表 3 qa=qb，a=，b=l时双模量简支梁中点处弯曲应力

参数 方法 l=h l=2h l=3h l=4h l=5h l=6h σx1本文方法 0.72 2.83 6.35 11.27 17.58 25.29 ANSYS 0.69 2.79 6.28 11.21 17.49 25.18 E1=E2=93.2 GPa 0.65 2.63 5.91 10.50 16.41 23.63 E1=E2=124.36 GPa 0.65 2.63 5.91 10.50 16.41 23.63 σx2本文方法 0.63 2.49 5.59 9.89 15.49 22.25 ANSYS 0.60 2.45 5.52 9.80 15.38 22.13 E1=E2=93.2 GPa 0.65 2.63 5.91 10.50 16.41 23.63 E1=E2=124.36 GPa 0.65 2.63 5.91 10.50 16.41 23.63

表 4 qb=2qa，a=，b=l时双模量简支梁中点处弯曲应力

表 4 qb=2qa，a=，b=l时双模量简支梁中点处弯曲应力

注：表1~表4中E1=E2=93.2 GPa、E1=E2=124.36 GPa是材料力学方法。

参数 方法 l=h l=2h l=3h l=4h l=5h l=6h σx1本文方法 0.95 3.77 8.48 15.02 23.45 33.71 ANSYS 0.92 3.71 8.39 14.91 23.29 33.45 E1=E2=93.2 GPa 0.88 3.50 7.88 14.00 21.88 31.50 E1=E2=124.36 GPa 0.88 3.50 7.88 14.00 21.88 31.50 σx2本文方法 0.82 3.30 7.43 13.20 20.58 29.68 ANSYS 0.80 3.26 7.35 13.09 20.46 29.42 E1=E2=93.2 GPa 0.88 3.50 7.88 14.00 21.88 31.50 E1=E2=124.36 GPa 0.88 3.50 7.88 14.00 21.88 31.50

本文把双模量梁应力公式的级数解、有限元法、材料力学方法计算的结果均列在表1~表4中，以便分析对比三种方法计算结果的计算精度。

由表1~表4可知，采用奇异函数研究分布载荷作用在双模量简支梁上任意梁段上的弯曲变形都是很方便的。本文方法与有限元法的计算结果相差不大，验证了本文方法的正确性。

相同弹性模量弹性理论与本文双模量简支梁中点处弯曲应力的级数解误差均在5%以上。对于双模量梁而言，采用单模量弹性理论研究双模量梁的弯曲应力，拉压区的弯曲应力绝对值是相等的，因为单模量弹性理论确定的梁的中性轴位置是在梁横截面高度的中点处。而事实上，双模量梁的拉压区的弯曲应力绝对值是不相等的，是随双模量简支梁拉压区的弹性模量变化而变化的，即双模量弹性理论确定的梁的中性轴位置不在梁横截面高度的中点处，从而导致双模量梁的拉压区的弯曲应力绝对值不相等。在本文中，双模量简支梁的拉压区的弯曲应力相差均达10%以上。所以，双模量简支梁的平面应力问题，不宜采用相同弹性模量弹性理论，而应该采用双模量弹性理论。

由于长高比的增大使得弯矩变大，因而，在外载荷作用下，双模量简支梁的弯曲应力随着长高比的增大而增大。

由于分布载荷作用下的弯矩大于均布载荷，相应的，双模量简支梁中点处的弯曲应力大于均布载荷。

由表3、表4可以看出，对于拉伸区的弯曲应力，材料力学方法与本文方法计算结果相差不大，压缩区的弯曲应力则误差较大，大于50%，说明了材料力学方法计算双模量简支梁的弯曲应力的局限性。

5 结论

（1）采用奇异函数研究分布载荷作用在双模量简支梁上任意梁段上的弯曲变形都是很方便的。本文证明了双模量梁中性轴的位置与作用在梁的横向载荷无关。

（2）采用奇异函数研究双模量简支梁弯曲应力，具有较高的计算精度。

（3）对于拉压弹性模量相差较大的简支梁，其平面应力计算要采用双模量弹性理论。

（4）在外载荷作用下，双模量简支梁的弯曲应力随着长高比的增大而增大；均布载荷作用下的弯曲应力小于分布载荷作用。