刘孝磊，顾丽娟，刘晓燕，郭立娜

（1.海军航空大学，山东烟台264001；2.南山学院，山东烟台265706）

自1983年，Cohen和Grossberg提出了一种广义的整数阶神经网络模型[1]

以来，对该类模型的研究就日益深入，并逐步推广到时滞Cohen-Grossberg神经网络模型[2]、Cohen-Grossberg神经网络模型鲁棒稳定性[3]、带随机项Cohen-Grossberg神经网络模型的研究。而在2009年，由Arefeh Boroomand和Mohammad B.Menhaj提出了分数阶Hopfield神经网络模型[4]：

式（2）中：i=1,2,…,n； 0＜α＜1；为Caputo型分数阶导数。

自此，分数阶神经网络伴随着分数阶微积分理论、分数阶微分方程及其稳定性相关理论的日渐成熟，对分数阶神经网络的稳定性研究也日益丰富[5-8]。而分数阶Cohen-Grossberg神经网络是分数阶Hopfield神经网络的一种推广，本文提出一类分数阶Cohen-Grossberg神经网络模型：

进而讨论了该类型Cohen-Grossberg模型稳定性的充分条件。

1 预备知识

定义1[9]：给定α∈ℝ，f()x的分数阶Caputo导数Dαf(x)定义为Dαf(x)=Jm-αf(m)(x)，其中m=[]α+1，，这里的Γ()为Γ-函数，即Γ(β)=

性质1：DαC=0，其中，C为常数。

性质 2：Dα(μf(t)+νg(t))=μDαf(t)+νDαg(t)，这里，μ、ν为常数。

定义 2[10]：Mittag-Leffler函数Eα(z)和双参数形式的Mittag-Leffler函数分别定义为：

从定义易得，Eα(z)=Eα,1(z)，并且E1,1(z)=ez。

考虑一般的分数阶系统：

定 义 3[11]：若xˉ=0 是 系 统 的 平 衡 点 ，且，其中λ＞0,b＞0,m(0)=0,则称系统的解是Mittag-Leffler稳定的。

引理1[12]：若x(t)为[0,+∞)上的连续可微函数，则

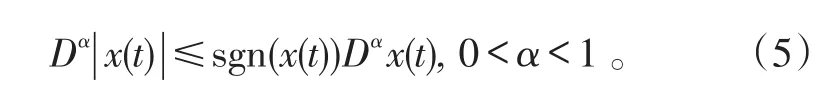
在[0,+∞)几乎处处成立。

引理2[13]：若V(t)为[0,+∞)上的连续函数，且满足DαV(t)≤θV(t)，0＜α＜1，θ为常数，则V(t)≤V(0)Eα(θtα)，t≥0。

2 主要结果

给出如下形式的分数阶Cohen-Grossberg神经网络模型：

式（6）中：x=(x1,x2,…,xn)T表示神经元状态变量；A(x(t))=diag[a1(x1),a2(x2),…,an(xn)]T表示放大函数；B(x(t))=[b1(x1),b2(x2),…,bn(xn)]T表示放大函数；C为神经元之间的互联矩阵；F(x)=[f1(x1),f2(x2),…,fn(xn)]T为激活函数。

对于函数ai(xi) 、bi(xi) 、fi(xi) 做如下假设。

H1：对于i=1,2,…,n，有

H2：对于i=1,2,…,n，fi(xi)满足Lipschitz常数为li的Lipschitz条件。

H3：存在μi＞0，使得

定理：若系统满足H1、H2，则x=0是系统的Mittag-Leffler稳定平衡点。

证明：构造Lyapunov函数

由分数阶导数的性质、引理1及假设H1、H2、H3得：

所以由引理2可得，

故则x=0是系统的Mittag-Leffler稳定平衡点。

3 实例仿真

为系统选取参数：

图1～3分别为x1(t)、x2(t)、x3(t)随时间t收敛于0的曲线图。

由仿真结果可以看出，系统的状态曲线明显收敛于稳定平衡点x=0。

图1 x1(t)的状态曲线图Fig.1 State curve ofx1(t)

图2 x2(t)的状态曲线图Fig.2 State curve ofx2(t)

图3 x3(t)的状态曲线图Fig.3 State curve ofx3(t)

4 结论

本文首先通过对分数阶Cohen-Grossberg神经网络的分析，给出了判定该类系统Mittag-Leffler稳定的充分性条件，并进行了Matlab仿真，通过具体实例验证了文中给出定理的正确性。