■刘大鸣（特级教师）

2018年高考对三角函数的考查主要是围绕“三角函数的图像变换，函数y=Asin（ωx+φ）和y=Acos（ωx+φ）的图像与性质，三角函数在区间上的零点，三角函数的最值”等展开的，彰显“整体变量观念、转化与化归和数形结合”素养的具体应用。

聚焦1：三角函数图像变换的思维方法

例1（2018年高考天津卷）将函数y=的图像向右平移个单位长度所得图像对应的函数（ ）。

解：由题意求出平移后的函数解析式，然后确定函数的单调区间。将函数y=的图像向右平移个单位长度所得图像的解析式为依据正弦函数的单调性，可得所求函数的单调增区间为即令k=1，得到一个单调增区间为同理可得单调递减区间为即令k=1，得到一个单调递减区间为应选A。

品味：三角函数的图像变换的两种途径：一是先伸缩后平移，二是先平移后伸缩。要注意的是：y=Asin（ωx+φ1）到y=Asin（ωx+φ2）的平移单位是当Δx＞0时，将y=Asin（ωx+φ1）图像上所有点向左平移Δx个单位得到，当Δx＜0时，将y=Asin（ωx+φ1）图像上所有点向右平移-Δx个单位得到。

变 式 1：已知函数f（x）=（其中ω＞0）的最小正周期为π。

（1）求ω 的值。

提示：（1）f（x）=由得ω=1。

聚焦2：函数y=Acos（ωx+φ）+B图像的应用

例2（2018年高考北京卷）设函数（ω＞0），若 f（x）≤对任意的实数x都成立，则ω的最小值为_________。

解：根据余弦函数取最大值的条件解得ω，进而确定其最小值。对任意的实数x都有成立，可知当时，函数f（x）有最大值，可得所以=2kπ（k∈Z），即又ω＞0，故

品味：理解y=cosx，y=Acos（ωx+φ）+B之间的关系，借助整体变量观念，利用余弦函数的性质可研究y=Acos（ωx+φ）+B的性质。

变式2：已知函数y=sin（2x+φ）的图像关于直线对称，则φ的值是_______。

提示：由 函 数 y=sin（2x+φ）的图像关于直线对称，可得所以即又故

聚焦3：求函数y=Asin（ωx+φ）+B 的周期及最值问题

（1）求f（x）的最小正周期。

解：（1）利用辅助角公式化为一个角和一种三角函数形式，再用周期公式求解。由于所以f（x）的最小正周期

品味：形如y=asinωx+bcosωx的函数，利用辅助角公式可化为形式，其最小正周期为

变式3：已知函数fx（）=sin2ωx+的最小正周期为π。

（1）求ω 的值。

提示：（1）函数

聚焦4：三角函数的解或零点问题

例4（2018年高考上海卷）设常数a∈R，函数f（x）=asin2x+2cos2x。

（1）若f（x）为偶函数，求a的值。

解：（1）若f（x）为偶函数，则对任意x∈R，均有f（x）=f（-x），即asin2x+2cos2x=asin2（-x）+2cos2（-x），化简可得方程2asin2x=0对任意x∈R都成立，故a=0。

若该方程在[-π，π]上有解，则k=0或k=1，对应方程的解x的值分别为

品味：三角变换中常用的降幂公式有：

变式4：函数在上的零点个数为_________。

提示：由题意可得所以即∈Z。当k=0时当k=1时当k=2时均满足题意。故函数f（x）在[0，π]上的零点个数为3。

聚焦5：三角函数的单调性问题

例5（2018年高考全国卷）若f（x）=cosx-sinx在[-a，a]上是减函数，则a的最大值是（ ）。

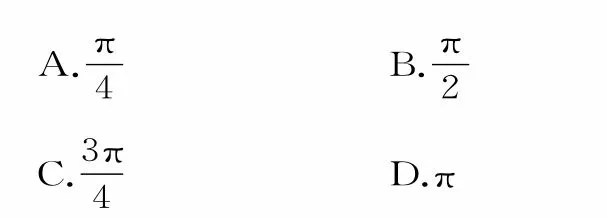
解：先确定三角函数的单调减区间，再根据集合包含关系确定a的最大值。由函数f（x）=cosx-sin且y=cosx在区间[0，π]上单调递减，可得0≤x+即

品味：求解三角函数的单调性，凸显整体变量的应用。

变式5：若f（x）=cosx-sinx在[0，a]是减函数，则a的最大值是（ ）。

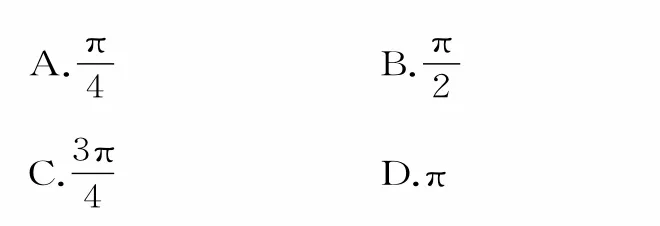
提示：由 f（x）=cosx-sinx=可得（k∈Z），即Z），所以所以0＜a≤即a的最大值为应选C。