基于滑动窗迭代最大后验估计的多源组合导航因子图融合算法

2019-05-08徐昊玮廉保旺刘尚波

兵工学报 2019年4期

徐昊玮，廉保旺，刘尚波,2

(1.西北工业大学电子信息学院, 陕西西安 710072； 2.中国科学院西安光学精密机械研究所, 陕西西安 710119)

0 引言

通过内部子导航系统间共享信息和性能互补，配备不同类型导航源的多源组合导航系统，能够在复杂环境中为各种平台提供连续且准确的导航解决方案。信息融合是多源组合导航系统中的最基本问题，近年来已有许多研究集中于各种导航源的相互融合，如全球卫星导航系统(GNSS)、惯性导航系统(INS)、激光测距(LiDAR)系统、磁力计、计算机视觉或超宽带(UWB)定位系统等[1-3]。在许多基于INS的多源组合导航系统中[4-6]，集中式卡尔曼滤波算法经常被用来处理所有观测量，并提供全局最优估计。尽管集中式卡尔曼滤波可以避免观测信息的丢失，但随着导航源数量的增多，急剧增加的计算负担和较差的系统容错性会使得整个融合系统的性能下降。

针对上述问题，联邦卡尔曼滤波器[7-8]作为一种分散化的卡尔曼滤波算法，逐渐受到关注。联邦卡尔曼滤波器由众多子滤波器和一个主滤波器组成，它是一种具有两阶段数据处理的算法。在进行多源组合导航数据融合的过程中，子滤波器将子导航源输出的导航观测量与参考导航源输出的导航解进行融合，从而得到局部导航状态估计值，而局部导航状态估计值和子系统协方差矩阵被输入到主滤波器中，计算全局最优估计并更新全局协方差矩阵。然而，由于不同子导航源之间异步的数据更新以及在线和离线传感器之间的切换，在主滤波器融合过程中各个局部导航观测量的时刻并不统一，导致引入全局估计误差。一些研究通过引入内插或递推的算法，将子系统的时刻统一，但也因此会引入人为误差，增加了计算负担[9]。

为了解决多源组合导航融合应用中存在的上述问题，文献[10-12]提出了一种基于因子图的多源组合导航信息融合算法。因子图算法(简称FG算法)是一种基于图的贝叶斯推理平滑算法[13]，它为即插即用型传感器提供了灵活的应用基础。在FG算法中，传感器网络中的每个观测量被编码成一个因子，所有传感器的观测因子通过节点互连的方式组成框架图，通过对这些连接在框架上的因子使用贝叶斯推理完成数据融合和参数估计。由于在多源组合导航系统中，各导航源更新观测量的速率不一致，因此采用更新速率最高的INS作为主导航源，当在某时刻从任意子导航源获取测量结果时，首先利用INS中的惯性测量单元(IMU)输出数据进行预积分和定位解算，来计算未知观测节点的预测值；然后将观测量作为后验信息，通过迭代得到各节点状态量的全局最大后验估计。文献[14]在此基础上进一步将滑动窗的概念引入多源组合导航因子图算法中。滑动窗使得因子图的全局最优化过程仅发生在最新生成的若干个节点间，它的引入不仅提高了融合算法的估计速度，而且减少了算法的计算量。

多源组合导航因子图融合算法的最优化过程是通过最小化观测量与预测量之间的马氏距离[15]实现的，马氏距离与子系统先验误差分布的均值向量和协方差矩阵相关，在上述FG算法[10-14]中，观测量的误差分布一旦完成初始化后将保持不变。然而，由于各种环境因素的影响，非惯性导航源的观测量是时变的，当融合算法中观测量误差的先验估计与实际得到的观测量存在差异时，就会导致估计结果相对于真实值存在较大偏差，因此需要引入算法对观测量误差进行实时的估计。基于以上原因，本文提出了一种基于高斯模型下的子系统观测量均值向量和协方差矩阵的估计算法，该算法能够通过迭代选权的方式对观测量误差分布状态进行准确、快速地估计，进而提高FG算法对导航状态估计的精度。

1 基于滑动窗的因子图组合导航系统模型

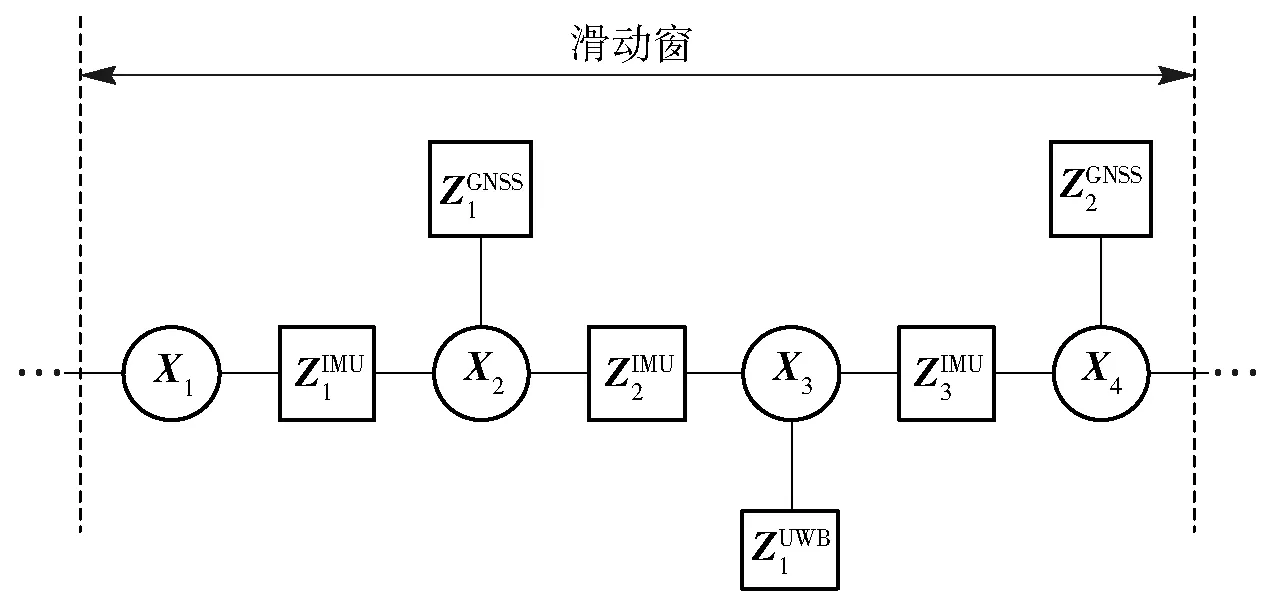
图1 多源组合导航FG算法的原理示意图Fig.1 Schematic diagram of factor graph-based multi-source integrated navigation data fusion algorithm

在FG算法中，应用贝叶斯推断进行状态量估计的范围可以是整个因子图网络，但是遍历估计的方法使得算法在运行过程中的计算量不断增大，而且最新得到的观测值对早期变量估计准确性的提高也并不显著。因此通过对因子图的优化范围加窗，即限定参与优化的因子节点范围，能够有效减少算法计算量、提高算法的效率。

滑动窗因子图意味着滑动窗口内仅包含全部因子节点中的一部分，它类似于固定滞后平滑算法。然而，与传统的线性平滑器不同，滑动窗因子图可以通过应用增量平滑算法，在每次产生新观测量时无需重新计算整个雅克比矩阵，仅需要对经过正交三角分解(QR)的雅克比矩阵进行增量更新即可。滑动窗FG算法中加窗的范围即是应用贝叶斯推断进行状态量估计的范围，滑动窗的滑动规则包括定步长、变步长和定窗长、变窗长[15]。滑动规则的选择一般与应用场景相关，如在动态性变化较大的应用场景中，一般采用定步长、变窗长的滑动规则，从而保证算法能够根据载体动态性自适应地调整估计值输出速率。而在本文的应用场景下，由于信号和载体运动状态的动态性变化相对较小，选取定步长、定窗长的滑动规则。本文中加窗的范围是通过设定观测量数目而确定的，即当观测节点达到设定上限时，则产生新的窗。

2 因子图组合导航融合算法

2.1 FG算法

为了实现导航系统中的数据融合，首先建立k时刻导航坐标系下的状态变量Xk为

(1)

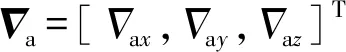
需要说明的是，之所以选用导航参数而非导航参数误差作为系统的状态量，主要是基于两方面的考虑：1)将导航参数作为系统状态变量，可以通过系统模型直接描述系统导航参数的动态过程，相比于根据1阶近似推导得到的基于导航参数误差状态量，导航参数能够更加准确地反映真实状态的演变[16]；2)对更新的IMU数据进行预积分和解算后，无需等待子系统观测量更新，可以直接建立因子节点并加入因子图中[7,18]。导航参数的微分方程为

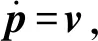
(2)

(3)

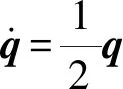
(4)

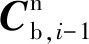
pi=pi-1+vi-1Δt，

(5)

(6)

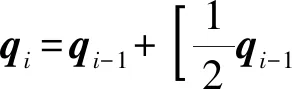
(7)

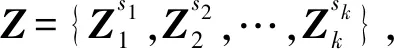
(8)

该后验概率密度函数似然概率密度f(Zi|Xi)和先验概率f(Xi|Xi-1)呈比例，即

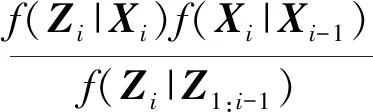
(9)

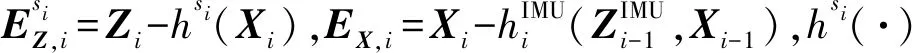
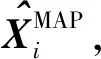
(10)

(11)

(12)

(13)

上述因子图编码的优化问题一般由高斯-牛顿迭代算法求解，(14)式所示为高斯-牛顿迭代算法的迭代规则[10]：

(14)

式中：ΔX=[ΔX1，ΔX2，…，ΔXk]；J()为包含滑动窗内所有节点的全局雅克比矩阵，

(15)

r()=[r1,r1,…,rk]为当前估计值下的观测量残差，

(16)

在高斯-牛顿迭代求解过程中，需要在每个迭代周期内应用最小二乘法计算ΔX的值，一旦计算得到ΔX，则将+ΔX的值作为下次迭代的初始值，若ΔX足够小或者超出迭代次数则取当前值作为最终的状态估计量。(15)式中JZ和JX的导数可以分别通过(17)式～(19)式计算得到：

(17)

(18)

(19)

2.2 增量平滑算法

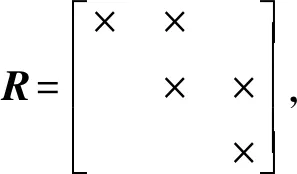
随着系统工作时间的逐渐增加，FG算法中产生的因子节点逐渐增多，而每次因子节点的产生都需要重新求解已有各个因子节点中状态量的最优估计值，但每次最优化过程都需要重新产生J矩阵，并对J矩阵进行QR分解，得到平方根信息矩阵R，以完成矩阵求逆和最小二乘解的计算，上述过程会带来较大的计算负担，也对系统的实时性造成了影响。

假设(20)式所示为通过QR算法计算得到的当前因子图的平方根信息矩阵R[10]：

(20)

式中：×表示矩阵中的非0元素。

当有新的因子节点产生时，对应的平方根信息矩阵R′为

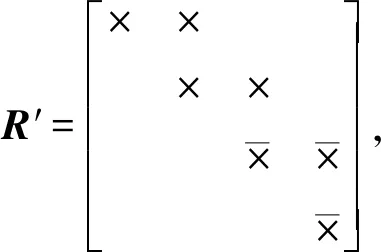
(21)

2.3 时变导航子系统观测量状态对FG算法的影响

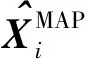
最大似然估计法是传统的μ和Σ的估计算法[18]，假设p为Xi的维数，m为样本数量，最大似然估计算法只有满足m≫p，才能得到较为准确的估计值。然而在多源组合导航的应用中，各导航源的观测量更新速率不同，且测量精度变化较快，如果应用最大似然类估计算法则会造成估计滞后或估计误差大的问题。最大后验估计在最大似然估计的基础上又增加了先验概率的辅助，而先验概率的加入使得估计在较小的数据集中能够保持有良好的泛化性能[19]。基于以上原因，本文在传统最大后验估计算法的基础上提出了一种应用于因子图的迭代型均值向量和协方差矩阵的最大后验估计算法。

3 均值向量和协方差矩阵的最大后验估计

3.1 导航状态分布参量的迭代最大后验估计

最大后验估计融入了待估计量的先验分布，因此最大后验估计可以看作规则化的最大似然估计。以观测误差EZ为例，为了在样本数量远低于估计量维度数量的情况下得到较为准确的μZ和ΣZ估计值，首先假设μZ和ΣZ服从Gaussian-Wishart分布，即(μZ,ΣZ)～NIW(μZ0,k0,v0,Ψ)，其中μZ0为μZ的均值，Ψ为ΣZ的先验值，v0为ΣZ的自由度，k0为μZ协方差的尺度因子，μZ与ΣZ的联合概率密度[20]可以表示为

(22)

式中：

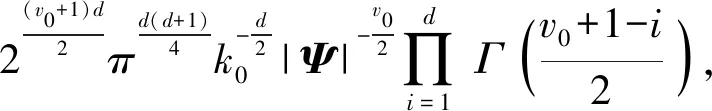
(23)

d为数据的维度数；μ0为所有导航源的均值向量。

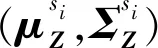
(24)

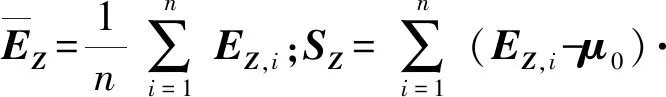
(25)

(26)

(27)

(28)

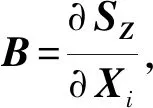
(29)

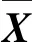
(30)

(31)

另外，在传统基于滑动窗的FG算法中，由于在优化过程中对状态量和观测量的分布不进行更新，当优化窗向前滑动时，无需进行特殊的操作，直接应用先验分布进行优化操作。但是在本文提出的基于迭代最大后验估计的因子图IMAPFG算法中，当窗向前滑动时，需要将上一时刻估计得到的状态量和观测量分布作为新窗中各个状态的先验分布，即μZ0和Ψ.

最后需要说明的是，对协方差矩阵的动态估计，实际上是一种动态加权的过程，即当某一时刻测量值的残差较大时，估计得到的协方差矩阵也会相应增大，因此在下一次迭代周期中起到了降低权值的作用。随着迭代的不断进行，对于该观测值的信任会不断下降，该过程有助于提高融合算法对于野值点干扰的鲁棒性。而算法中对于均值向量的估计一方面能够提高协方差矩阵估计的准确性，另一方面，则能很好地解决由观测量偏置而引起的融合算法异常的问题。

综上所述，本文所提出的IMAPFG算法步骤为：

1) 设置各导航系统与因子图初始参数，并定义状态空间向量，确定滑动窗范围。

2) 当子导航系统输出测量值时，首先产生新的状态节点加入因子图中，并应用(5)式～(7)式根据IMU系统的观测量计算该状态节点的初始值，同时将产生观测节点连接到该状态节点上。

3) 判断是否满足滑动窗口范围：当超出窗口范围时，向前滑动窗或产生新的窗，并将上一窗内估计得到的状态量和观测量分布作为当前窗的先验估计；当满足滑动窗口大小时，则直接进行步骤4.

4)应用(14)式对窗口范围内的因子图进行最优化融合，并根据(27)式～(31)式对各系统的协方差矩阵和均值向量进行更新，当达到迭代次数上限或者残差足够小时退出迭代。

5) 输出滑动窗内各状态节点的状态估计值，将各系统的协方差矩阵和均值向量的最终估计值作为下一个滑动窗内各参量的初始值，滑动窗向后移动l个节点，返回步骤2.

3.2 迭代更新对最优化系统收敛性的影响

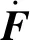
在FG算法中，非线性算子F为多个因子节点根据(5)式～(7)式进行状态更新的集合，对F关于各个因子节点状态求导，即可得到J矩阵，因此F可导。在3.1节中提出的最优化算法中，J矩阵在每个迭代周期内都根据观测值进行调整，分析(15)式与(17)式～(19)式可知，新算法对J矩阵的调节相当于对矩阵中的各行元素分别乘以一个常数，如(32)式所示：

(32)

式中：Ji为矩阵J的第i行；ai表示新算法对矩阵J中第i行的调节系数。根据矩阵行列式的性质可知J′的行列式满足：

(33)

4 测试实验设置

为了验证本文提出的IMAPFG算法的性能，分别进行了仿真测试与实验测试。在仿真测试中产生了不同种类的传感器测量变化，并将融合结果与真实参考值比较，可以定量地评价各种算法的优劣；而在实验测试中，则应用了真实的传感器数据验证融合算法的性能。

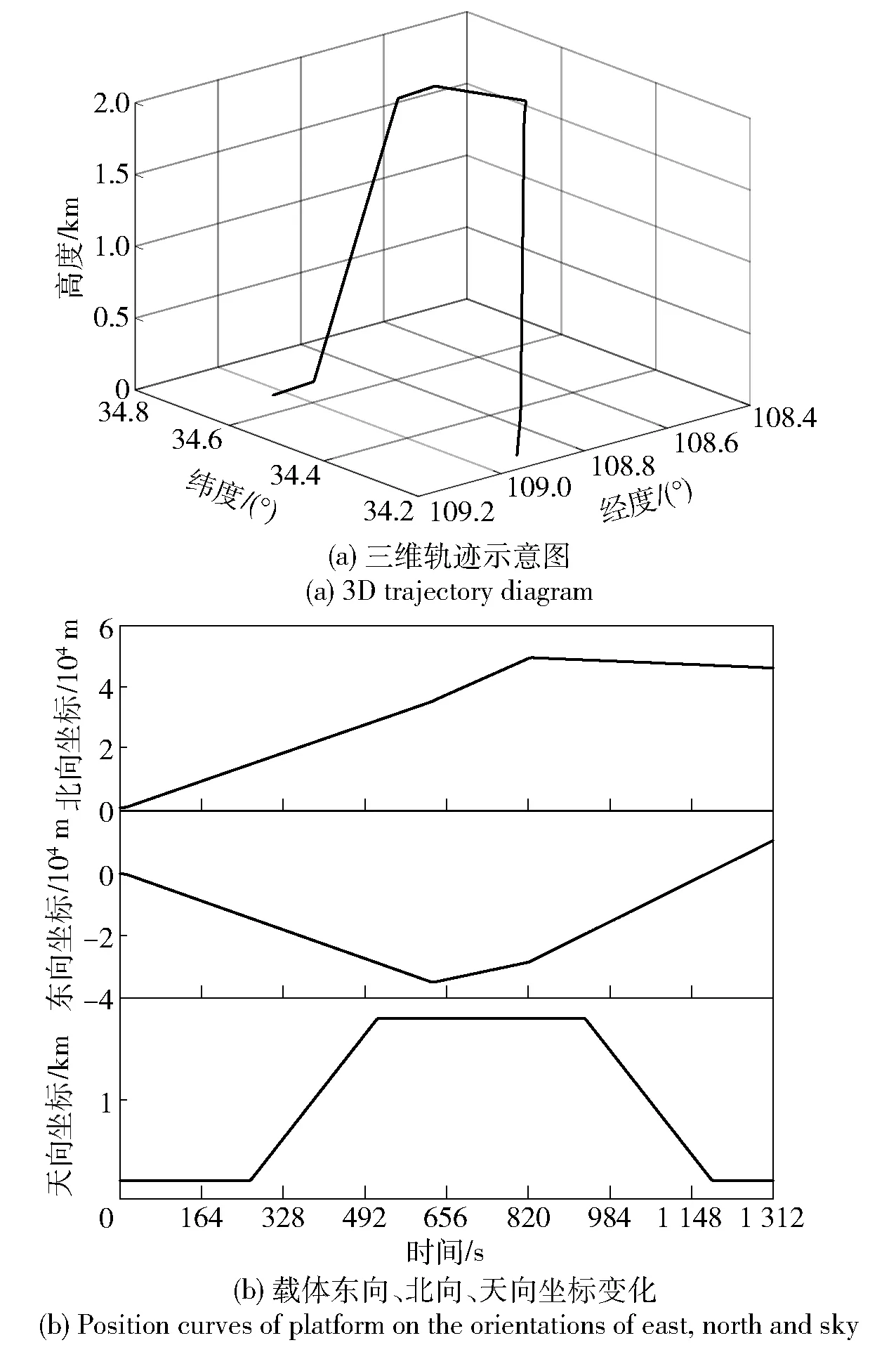
图2 载体运动轨迹图Fig.2 Trajectory diagram of platform

在仿真测试中，共产生了1 312 s的载体轨迹，轨迹中包括加速、减速、上升、下降、转向等多种载体运动方式，如图2所示为所产生的载体三维轨迹图和东向、北向、天向轨迹曲线。根据载体轨迹分别模拟产生了INS输出、GNSS输出、LiDAR导航系统输出和磁力计导航系统输出，各模拟导航源的详细规格如表1所示。为了验证各算法对导航源变化的处理性能，需要在各个子导航源中模拟观测量状态变化过程：对于LiDAR系统而言，轨迹中载体的上升与下降过程会导致LiDAR系统中用于地图匹配的特征点数量、匹配准确度下降，从而影响输出的载体位置精度[3]；对于GNSS与磁力计则人为地分别在特定时间段加入了偏置与噪声。为了更好地验证算法在不同子系统状态变化情况下的性能，在仿真实验中分别设置了两种测试方案：在方案1中各个时刻内有且只有1种子导航源状态发生变化，且变化方式均为突变；方案2中的子导航源状态变化形式更加复杂，在同一时段内最多有3种导航源同时发生变化，且变化形式也包含突变和渐变两种。表2展示了仿真实验中两种方案下各导航源的变化情况。在仿真测试中，分别应用本文所提出的IMAPFG算法、普通FG算法[10]、基于最大似然估计的因子图(MLEFG)算法[22]和基于传统最大后验估计的因子图(MAPFG)算法[19]对各个导航源输出数据进行融合，并比较融合结果。由于最大似然估计需要较大的样本空间才能得到较好的估计结果，对于MLEFG算法，每100个样本值才对各导航源的分布状态进行更新。在最大后验估计中，由于加入了先验信息，无需大量样本也能得到准确的估计值。在MAPFG算法中，每10个样本值就对导航源的方差和均值进行更新。IMAPFG算法的均值和方差是随着窗的滑动进行的，在仿真中3种算法的窗的大小都被设定为10，即每当产生10个观测值后进行因子图数据融合。另外，为了更符合实际情况，初始化的各子导航源的协方差矩阵都与仿真的数据有所偏差。

表1 仿真测试中各导航源参数Tab.1 Specifications of navigation sources for simulation test

表2 仿真测试中导航源观测值变化设置Tab.2 Setting of observation values

实验测试中所用的载体平台如图3(a)所示，图中手推车用于搭载Novatel GNSS天线，惯性测量单元 (IMU)和UWB无线电单元，所有传感器都通过脉冲秒(PPS)信号与GPS时间同步。 UWB网络由6个节点组成，UWB测量结果与GNSS测量结果由笔记本电脑记录。实验中UWB系统的输出频率为10 Hz， GPS系统的输出频率为2 Hz，磁力计输出频率为10 Hz，表3列出了实验中所用IMU的具体规格参数。在实验测试中，手推车在36 m×5 m的区域内进行折返运动，实验时间约为1 500 s. 手推车的运动轨迹如图3(b)中所示，实验场景被选在了植被覆盖的边缘区域，在此区域内，IMU、UWB和磁力计的导航输出保持稳定，但植被的遮挡会造成GPS系统的定位精度下降，或出现固定位置误差偏置等问题。为了量化各融合算法对于处理子系统观测状态变化的性能，在实验环境中，IMU、UWB与磁力计基本不受到外界因素的影响，因此观测量有较高的准确度，故采用以IMU/UWB/磁力计3种导航源的标准因子图估计轨迹作为导航状态参考真实值，相比于应用实验中标记的载体轨迹作为参考真实值，这样的设置可以增加速度与姿态的定量对比，同时也避免实验过程中由于人为操作带来的误差。之后分别应用不同融合算法计算得到IMU、UWB、GPS、磁力计4种导航源组合的估计轨迹，并与真实轨迹进行比较。在实验测试中，用于比较的融合算法种类与仿真实验中一致。

图3 实验场景Fig.3 Experimental scene

在仿真与实验测试中分别用到了GNSS、LiDAR、UWB和磁力计4种子导航源。由于各子导航源的工作原理不同，输出的导航观测量与对应的量测方程也有所不同。以下分别介绍4种子导航源对应的量测方程。

对于本文中仿真和实验所用的GNSS、LiDAR、UWB导航系统，输出的观测量都为载体的位置参数，因此这3种子导航源量测方程可分别表示为

表3 实验测试中MEMs和IMU系统参数Tab.3 Specifications of MEMs and IMU for experimental test

(34)

(35)

(36)

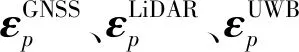
磁力计可以通过粗对准、坐标转换、磁航向计算、四元数更新和循环计算磁航向等步骤输出连续的载体姿态观测信息。需要说明的是，磁力计在粗对准过程中需要利用加速度计测量值来简单计算横滚角以及俯仰角，之后对磁数据完成坐标转换，并计算航向角；而在循环计算磁航向步骤中，磁力计仍需要从惯导系统中取得横滚角和俯仰角才能完成磁航向的计算。虽然磁力计实际上只提供了航向角的观测信息，但将测量航向角、横滚角、俯仰角转化为四元数后，则视为产生了四元数观测值。

基于上述分析，磁力计的量测方程可表示为

(37)

5 测试结果和分析

在融合算法中协方差矩阵的迹可以用来表示观测量的准确性，迹的值越小说明观测量误差越小，越可以信赖，反之则误差越大，越不可信。图4展示了在仿真测试方案1中，当分别应用MLEFG、MAPFG和IMAPFG 3种融合算法时，LiDAR导航系统协方差矩阵迹的变化曲线，图中用A、B、C、D 4个区域标记了表2中定义的子导航源变化区间。从图4中可以看出，MLEFG算法由于需要的观测样本大，对于LiDAR观测量的估计与真实情况有较大延迟。而IMAPFG算法与MAPFG算法则能够较为快速地对观测量变化做出反应，且IMAPFG的协方差估计值更为稳定，曲线更加平滑，估计性能更好。特别地，当进入区域B时，受到GPS偏置的影响，3种算法对协方差矩阵的估计都出现跳变，但是由于IMAPFG算法能够在迭代过程中实时更新均值向量，IMAPFG算法的协方差矩阵估计值受到均值变化的影响也较小，相应地，IMAPFG算法对GPS均值向量的估计也更加快速、准确。

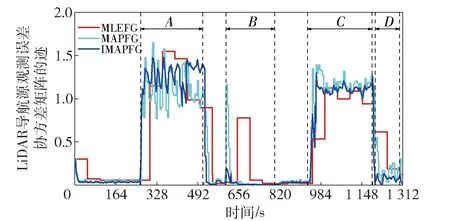
图4 LiDAR导航源观测误差协方差矩阵的迹的变化曲线Fig.4 Trace curves of covariance matrix of LiDAR navigation observation error

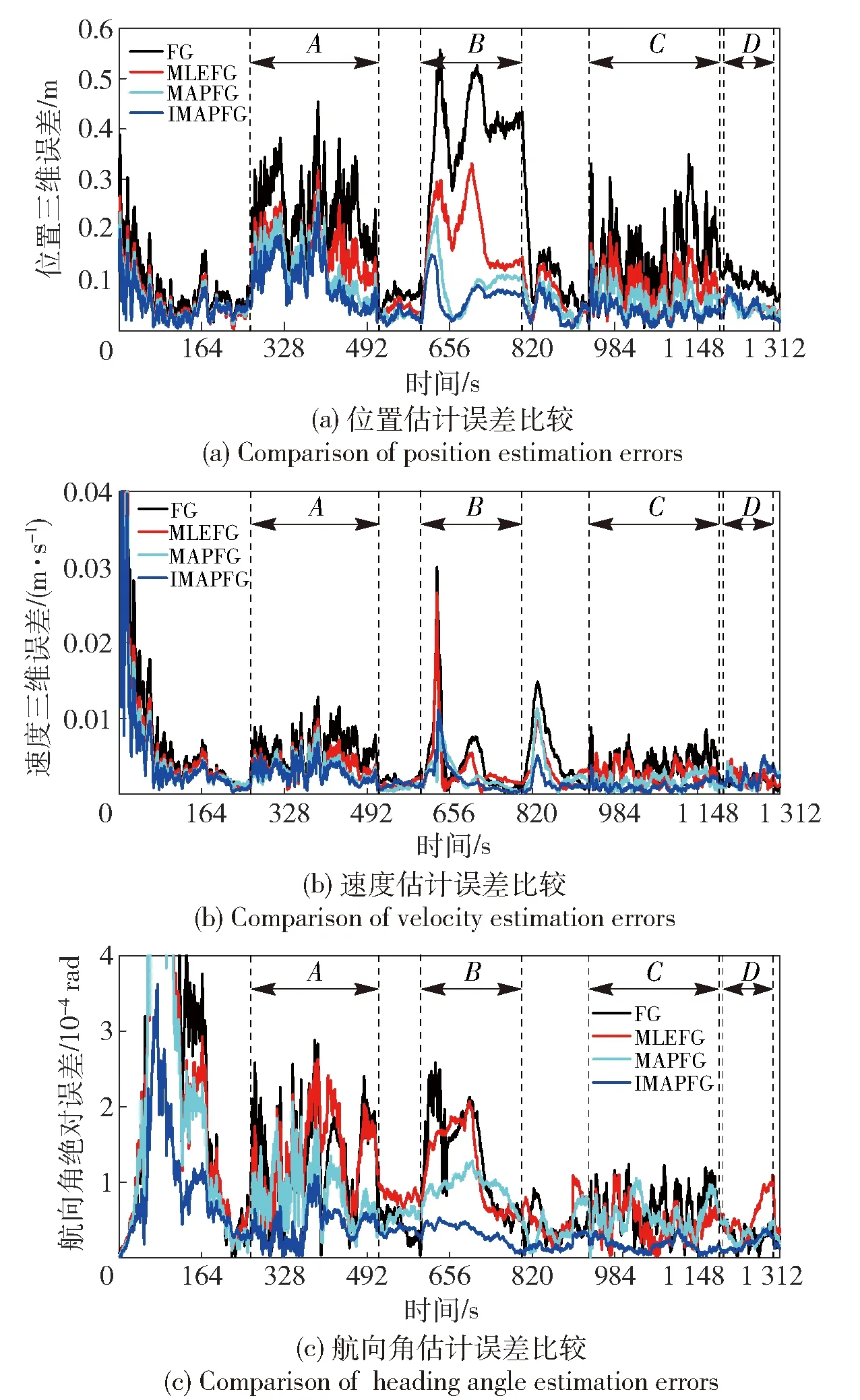
图5 仿真测试方案1中各算法的载体位置、速度、航向角的估计误差变化曲线Fig.5 Estimation error of the position, velocity and heading angle of algorithms in the simulation test of Scenario 1

如图5所示为仿真测试方案1中应用不同算法得到的载体位置、速度、航向角的误差变化曲线。从图5中可以看出，在开始阶段，各导航源相对稳定时，4种导航融合算法的性能差别较小。但是，由于在各个子导航源的初始方差中人为地加入了误差，相比于传统的FG算法，具有方差估计功能的其他3种融合算法对载体位置、速度、航向角的估计更加精确。随着导航源状态的变化，所有融合算法都受到一定程度的影响，各导航状态估计值的精度均有所下降。其中FG算法受到的影响最大，且在各状态各区域内，子导航源状态变化所带来影响并没有随着时间推移而减弱。相比于FG算法，其余3种算法都能逐渐降低子导航源变化带来的影响。以区域A为例，当LiDAR导航源输出的载体位置精度降低时，3种算法通过不同的方式逐渐提高LiDAR导航源的协方差值，从而在融合过程中减小对LiDAR导航源输出数据的依赖。由于基于最大后验估计的MAPFG算法与IMAPFG算法能够更加迅速地对子导航源的变化作出准确反应，对导航状态量的估计更加准确、受到子系统影响更小。进一步，由于在IMAPFG算法中，协方差矩阵和均值向量的最大后验估计过程是在迭代过程中完成的，在每次导航状态的估计中，残差与子系统状态信息相互影响，保证了估计值的最优性，从而使得每次对协方差矩阵、均值向量相比于MAPFG算法都更加准确。从图5中也能看出，相比于MAPFG算法，IMAPFG算法对于子系统变化的反应更快，对导航状态量的估计更加准确。

表4中定量地展示了4种算法在方案1中各个区域以及全部轨迹中导航状态量的估计误差情况。从表4中可以看出，相比于另外3种算法，由于缺少对各子系统观测量状态的更新，FG算法在A、B、C、D 4个区域内输出的位置、速度和航向角的估计精度都明显低于其他3种算法，而在整个仿真轨迹中，FG算法的平均位置误差为0.17 m，平均速度误差为0.57 cm/s，平均航向角误差为，均为4种算法中最大。而IMAPFG算法，由于能够对子系统状态实时、准确地更新，从而能够更好地应对子系统观测状态的变化或恶化，其平均位置估计误差仅为0.05 m，相比于MAPFG算法、MLEFG算法、FG算法，IMAPFG算法的定位精度分别提高了28%、50%和71%. 除了定位精度外，IMAPFG算法的定速精度与定姿精度也有显著提高。

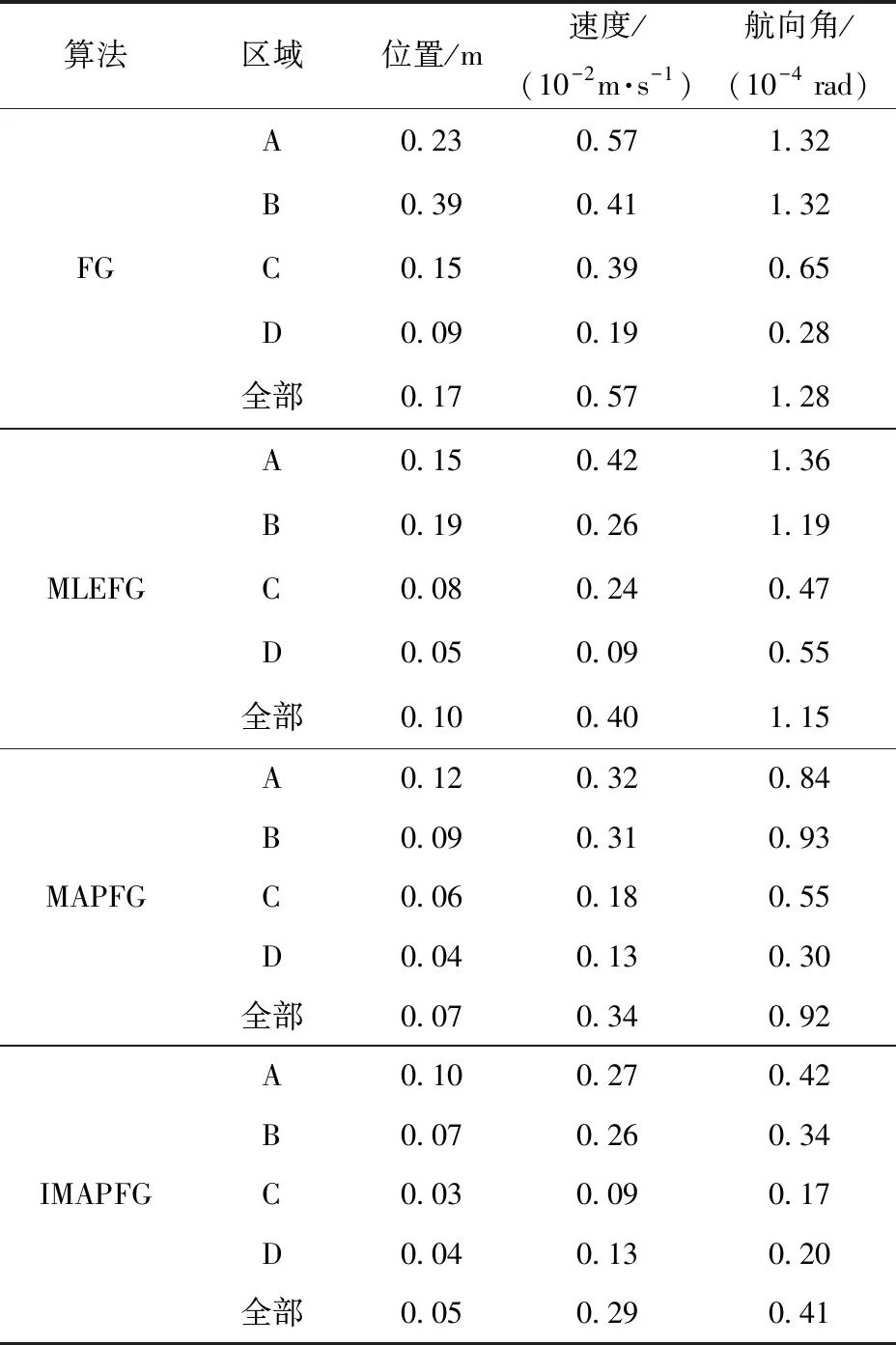
表4 仿真实验中各区域以及全部轨迹中导航状态量的估计误差Tab.4 Estimation errors of navigation state in different regions and whole trajectories in simulation experiments

图6 仿真测试方案2中各算法的载体位置、速度、航向角的估Fig.6 Estimated errors of position, velocity and heading angle of algorithms in Scenario 2

图6中展示了仿真测试方案2中应用不同算法得到的载体位置、速度、航向角的误差变化曲线。横向对比图5中各个算法的导航误差结果可知，图6中更为复杂且持续时间更长的子系统时变状态导致各算法的最终导航精度都恶化较多，特别是在有多个子导航源同时产生变化的H区域内时。但纵向对比各算法之间的性能可以看出，由于对仿真中GNSS子系统均值向量和协方差矩阵更加准确地估计，IMAPFG算法在各种导航状态的估计都更加准确。在方案2中，IMAPFG算法输出的位置三维误差均值、速度三维误差均值和航向角无误差均值分别为0.13 m、0.4 cm/s和4.8×10-5rad. 在方案2中，相比于MAPFG算法、MLEFG算法、FG算法，IMAPFG算法的定位精度分别提高了31%、63%和86%.

在实验测试中，如图7(a)中所示为实验测试中根据IMU、UWB、磁力计3种导航源估计得到的手推车运动轨迹，在实验中将该轨迹视为真实轨迹。手推车在实验人员的操作下在开阔区域与植被遮挡区域间做折返运动，遮挡区域如图7(a)中阴影部分所示，图7(a)中J、K红色矩形框标记区域分别为开阔区域下轨迹和遮挡区域下轨迹，图7(b)与图7(c)分别为矩形框J、K标记区域的放大图，图中蓝色圆点表示GPS的载体位置观测值。从图7中可以看出：在J区域下，GPS的测量值与轨迹基本保持一致，且抖动较小；而在K区域下，受到植被遮挡的影响，GPS输出的位置观测值受到较大影响，相比于区域J，可以明显看出区域K内GPS的观测值抖动更大且伴有一定的偏置。

表5中定量地展示了应用不同算法计算得到的IMU/UWB/GPS/磁力计多源组合导航系统的导航状态量的估计误差。从表5中可以看出，在开阔区域内，由于能快速、准确地估计子导航源的观测精度，IMAPFG算法拥有最小位置、速度、航向角估计精度。而相比于开阔区域，4种算法在经过遮挡区域时，导航精度均有所下降，这主要是由于GPS观测值在遮挡区域内恶化而引起的。但是，相比于其他3种算法，IMAPFG算法的定位精度恶化程度最低，IMAPFG算法的定位精度仅下降了18%，而对于MAPFG、MLEFG和FG算法而言，定位精度分别下降了28%、29%以及31%. 横向比较各算法的导航精度可以看出，IMAPFG算法在整个实验测试轨迹内拥有最优的导航精度，相比于MAPFG、MLEFG和FG算法， IMAPFG算法的定位精度分别提高了25%、59%、60%. 另外，除了定位性能外，无论在开阔区域还是遮挡区域内，IMAPFG算法的定速与定姿精度也均为最优。

另外需要说明的是，虽然在仿真测试中生成的INS与实验测试中应用的INS精度相差近10倍，但是融合结果却相差不多，这主要是由于更新频率和子系统精度的差异引起，具体有以下两点原因：一方面，实验测试中采用UWB系统代替LiDAR系统，而UWB系统能够提供更新频率更高的子系统观测量(10 Hz);另一方面，在实验测试中采用INS、UWB、磁力计3种导航源应用标准FG算法计算得到的融合结果作为参考真实值，而当再次使用以上3种导航源数据作为观测量时，就使得它们的测量值与视为参考真实值的导航结果较为接近，即相对精度更高，因此导致相对于该参考真实值的导航精度较高。