杜仁杰，苏 中，刘 宁，李 羚

(北京信息科技大学,高动态导航技术北京市重点实验室，北京 100101)

0 引言

在导航、制导与控制领域中，MEMS陀螺的固态设计使其更适用于高过载、高转速环境下的角速率测量。在通常的使用场合下，MEMS陀螺的量程一般为每秒几百度左右。但在短时多变速的高过载环境下，需要MEMS陀螺敏感角速率的能力最高达到每秒几千度左右。在该大量程角速率范围内，大量实测数据表明MEMS陀螺标度因数的线性度明显变差[1-3]，这将不能保证陀螺在相当大的动态范围内具有较高的输出精度。

传统非线性误差补偿方法通常针对低转速范围内MEMS陀螺的输出，对其线性区间内的数据进行低次拟合[4-5]，忽略了在大量程转速范围内的非线性问题。本文针对MEMS陀螺在短时多变速环境下的输出(角速率≤3 600°/s)呈现严重的非线性状态的现象，建立了回归方程，提出启发式分段回归拟合的补偿方法，对全量程下测量的角速率数据进行非线性回归拟合处理，有效提高了其非线性误差补偿精度，满足短时多变转速等高动态测量环境中对MEMS陀螺的高精度输出要求。

1 标度因数非线性误差模型

标度因数非线性误差是衡量MEMS陀螺产品精度和稳定性的重要指标之一。其含义是指在输入角速度范围内，陀螺输出量相对于最小二乘法拟合直线的最大偏差值与最大输出量之比。

MEMS陀螺输入输出关系典型模型表示为

Fi=KΩj+F0+vj

(1)

式中：Fj为第j个输入角速度Ωj时陀螺仪输出值，V；K为标度因数，V·(°)-1·s-1；Ωj为输入角速度，(°)/s；vj为拟合误差；F0为拟合零位。

用最小二乘法可求出K、F0：

(2)

(3)

得到K、F0后可构建由拟合直线表示的陀螺输入输出关系：

(4)

可分别按式(5)、式(6)计算输出特性的逐点非线性偏差、标度因数非线性误差来衡量所建模型的质量。

(5)

式中：αj为第j个输入角速度Ωj时，输出值的非线性偏差，%或ppm；Fm为陀螺仪输出的单边幅值。

Kn=max|αj|

(6)

式中Kn为标度因数非线性误差，%或ppm。

2 多模型标度因数的建模与补偿

标度因数补偿是用软件方法对陀螺标度因数产生的误差进行修正，补偿因标度因数非线性引起的不理想输出值。因此必须建立相关的大量程下转速拟合模型，对MEMS陀螺的测量数据进行曲线拟合。

2.1 传统多项式的补偿方法

多项式拟合是最常用的曲线拟合与回归方法之一。拟合曲线公式如式(7)所示：

Y(x)=a0+a1x+a2x2+…+anxn

(7)

式中：x为转台理想输入速率yi下相应的陀螺输出角速率；Y为拟合角速率；a0，a1，…，an为所建模型的参数。

其偏差为

(8)

I最小时的Y(x)即为所求的回归方程。令偏导数等于零：

(9)

可得到关于a0，a1，…，an的线性方程组，从中解算出ak(k=0,1,…,n)，从而可获得对应阶数为n的回归方程。

2.2 启发式分段多项式的补偿方法

传统多项式的补偿方法是对全量程下测量的角速率数据进行统一的非线性拟合处理。启发式分段回归拟合的补偿方法，分析了高转速全量程数据非线性特点的差异，得出分段点，确定MEMS陀螺的线性区与非线性区；最后针对不同区域数据特点建立相关的大量程下的分段转速回归模型，并对其模型进行连续性处理。

2.2.1 分段点确立方法

第一步：从零开始正向、反向逐渐扩大转速区间，根据陀螺理想输出值和实际测量数据，计算各转速区间下的非线性误差。

第二步：在逐渐扩大范围的转速区间下，计算相邻区间非线性误差差值的绝对值，记作|差|，再次做差，判断相邻|差|的差的符号，若为正则计数器增1。当连续计数不小于3时，则从第1个点处进行分段；否则不进行分段，计数清零。

第三步：根据分段结果分析各区间数据特点，确定其回归模型。

分段拟合流程图如图1所示。

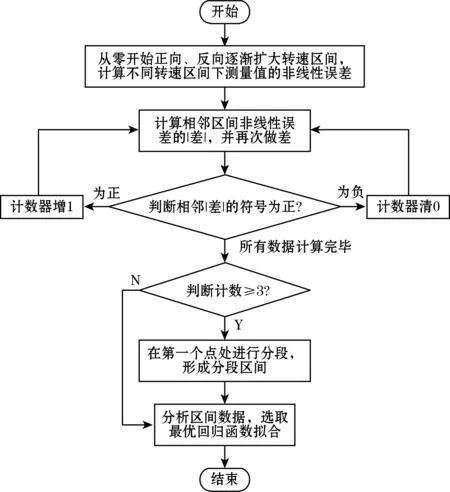
图1 分段拟合流程图

该分段补偿模型为：

(10)

2.2.2 分段拟合曲线的连续性分析

为了进一步减小分段点附近的拟合误差，保证分段拟合曲线的连续性。使用Hermite插值法[7]对其进行连续性处理，从而减少拟合曲线在分段点附近的偏移量，具体步骤为：

第一步：根据分段结果取第一段拟合数据为(xi,y)，i=1,2,3，…，q,用相应的回归模型阶数对其进行拟合，得到拟合曲线f1(x)。将拟合后的数据离散，得到离散点(xd,yd),d=1,2,3，…，n。

第二步：针对(xi,yi)及(xd,yd)，d=n-4,n-3，…，n,i=q,q+1,…，2q,对(xn-4,yn-4)进行加权并对加权之后的数据再次拟合，得到拟合曲线f2(x)。针对拟合曲线f2(x)，从点[xn-4,f2(xn-4)]开始离散处理，得到离散点(xd1,yd1),d1=1,2,3，…，n1。

第三步：针对(xd,yd),d=n-4,n-3，…，n及(xd1,yd1),d1=1,2,3，…，n1为两段拟合的重合部分，用插值曲线对其进行表示，实现其连续。以(xn-3,yn-3)及(x4,y4)为端点，确定插值曲线形式为：F=a1x3+a2x2+a3x+a4，其满足端点条件如下：

H(xj)=yj,H′(xj)=mj(j=0,1)

(11)

其中插值曲线系数a1、a2、a3、a4可以通过约束条件[7]求得。插值曲线在端点处一阶连续，所以保证实现曲线分段处的连续性。对分段数据依次进行处理，可得到一条连续的分段回归曲线。

3 实验验证与对比分析

测量系统包括：具有高精度输出的双轴转台系统、MEMS陀螺输出测量及数据传输系统、以及数据采集与分析系统、MEMS陀螺供电系统等。

选取动态范围为0～3 600°/s大量程MEMS陀螺为试验对象，将其连同工装水平固定在速率转台，X轴朝上作为标定敏感轴。陀螺上电预热20～30 min。然后分别给转台输入3 600、3 240、2 880、2 520、2 160、1 800、1 440、1 080、720、360、0、-360、-720、-1 080、-1 440、-1 800、-2 160、-2 520、-2 880、-3 240、-3 600°/s共21个角速率。连续采集每个角速率稳定后1～2 min陀螺输出数据，采样频率200 Hz。

由实验结果得到全量程下MEMS陀螺输出的原始数据，结果如图2所示。取实验数据中速率转台各输入速率下对应的陀螺输出数据，得到转台输入角速率与陀螺输出角速率的关系如图3所示，其具体数值见表1。

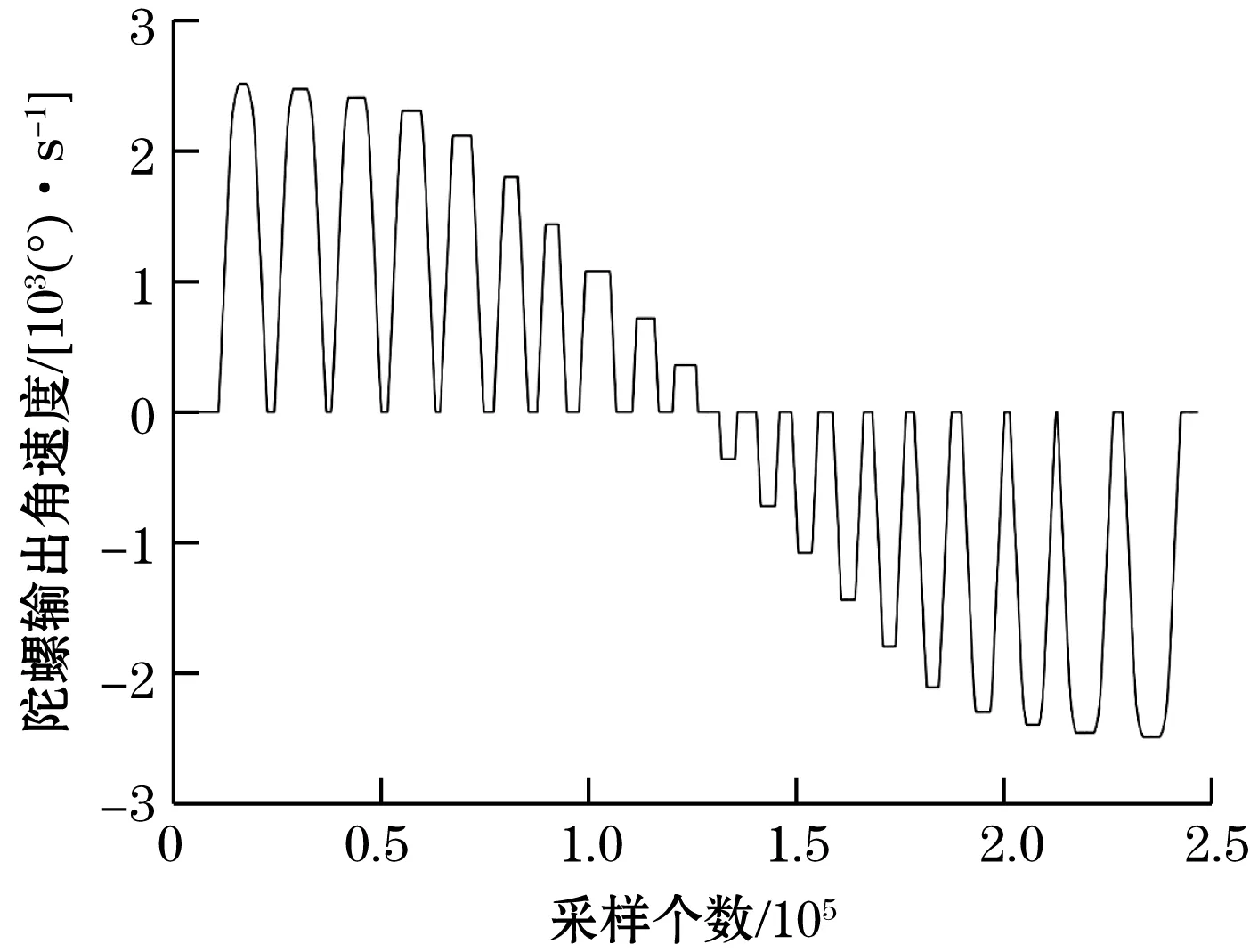
图2 不同转速下MEMS陀螺输出原始数据

图3 转台输入角速率与陀螺输出角速率的关系

从图3及表1的数据可分析出，介于受未知的外部环境和内部因素影响，MEMS陀螺样机的输出在低转速范围内具有较低的非线性误差，然而，当转速输入至高转速时，其输出呈现严重的非线性状态，标度因子非线性误差较大。但其信号中常含有一定趋势项，同一MEMS陀螺样机的非线性曲线存在相似性，可以通过对非线性曲线的拟合，归纳出其中隐含的函数关系，推导出拟合曲线的回归方程，对MEMS陀螺样机的标度因数非线性误差进行补偿。其中表1中测量值为多组测量值的平均值。

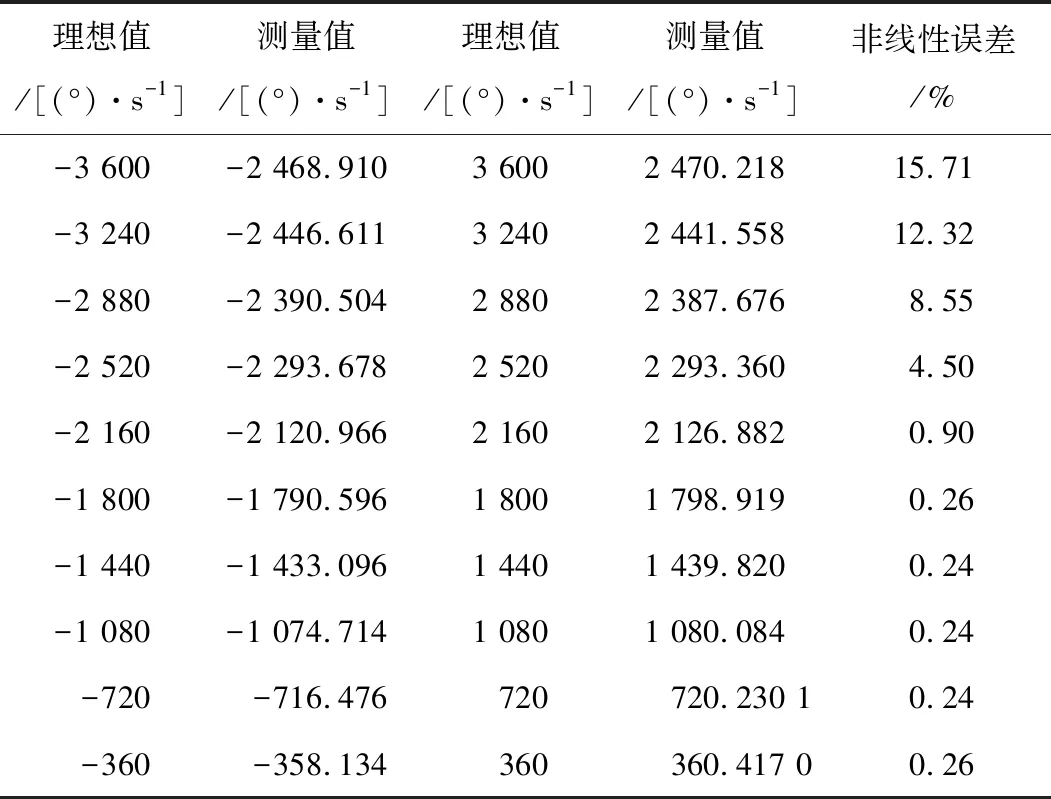
表1 陀螺理想输出值与实际测量输出值

通过表1分析陀螺全量程下的测量数据，可以发现低转速下数据的非线性程度很小，随着转速升高至某个临界点，非线性程度开始迅速增大。对于具有多个显著局部特征的数据，使用一个拟合函数来描述难以取得较好的拟合精度。由图3及表1所示的多组数据可通过式(5)和式(6)计算出MEMS陀螺样机输出数据的标度因数非线性误差的平均值为15.71%。分别对多组数据进行分段多项式回归拟合、Bayes-BP神经网络回归拟合及二次九阶多项式回归拟合。

其中Bayes-BP神经网络[10]回归拟合利用给定的学习集样本对网络进行训练，设定隐层节点个数为10。得到基于Bayes-BP神经网络的补偿模型。该方法使MEMS陀螺标度因数非线性误差提高了2个数量级，达到0.45%，耗时37.8 ms。

二次九阶多项式回归拟合是将陀螺原始输出进行九阶多项式拟合后，将该拟合输出再次作为输入向陀螺理想输出做第二次九阶多项式拟合。该方法使MEMS陀螺标度因数非线性误差提高了2个数量级，达到0.59%，耗时0.755 ms。

在分段多项式回归拟合方法中，通过启发式分段方法将数据分为3个区间：负方向高速率段、低速率段、正方向高速率段，其计算过程如表2所示。

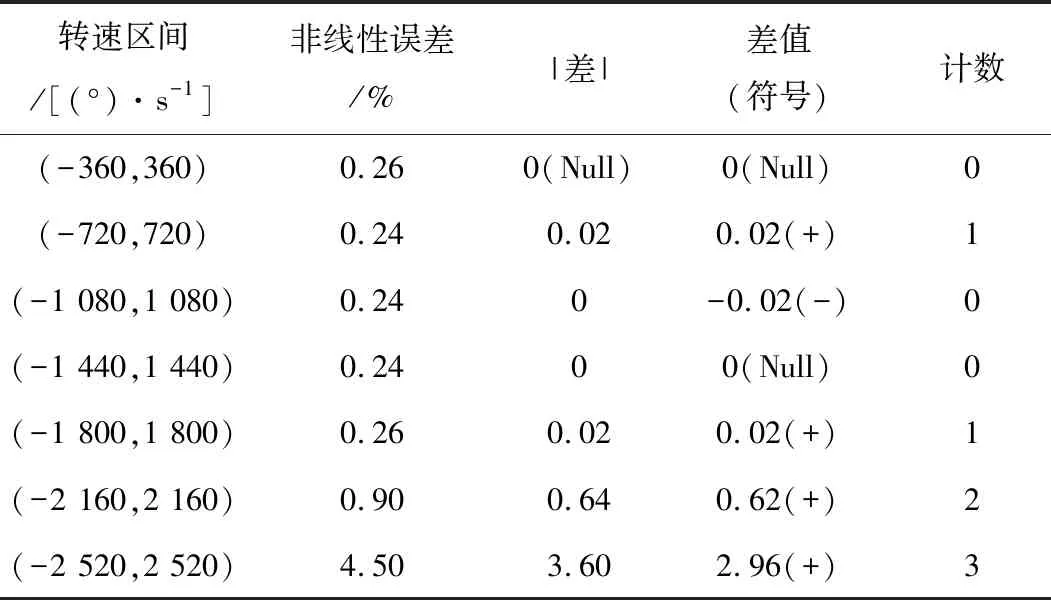
表2 分段点的实际计算过程

得到分段点-1 800°/s及1 800°/s。由于在低速率段数据具有良好的非线性误差，标度因数非线性误差在10-3数量级，满足MEMS陀螺实际的应用需求，所以对于此段数据采用低阶多项式；针对负、正方向高速率段，选用九阶多项式进行回归拟合，分段模型阶数为九阶-一阶-九阶。为进一步保证分段模型的连续性，使用Hermite插值法对其分段处进行连续性处理，效果如图4所示。

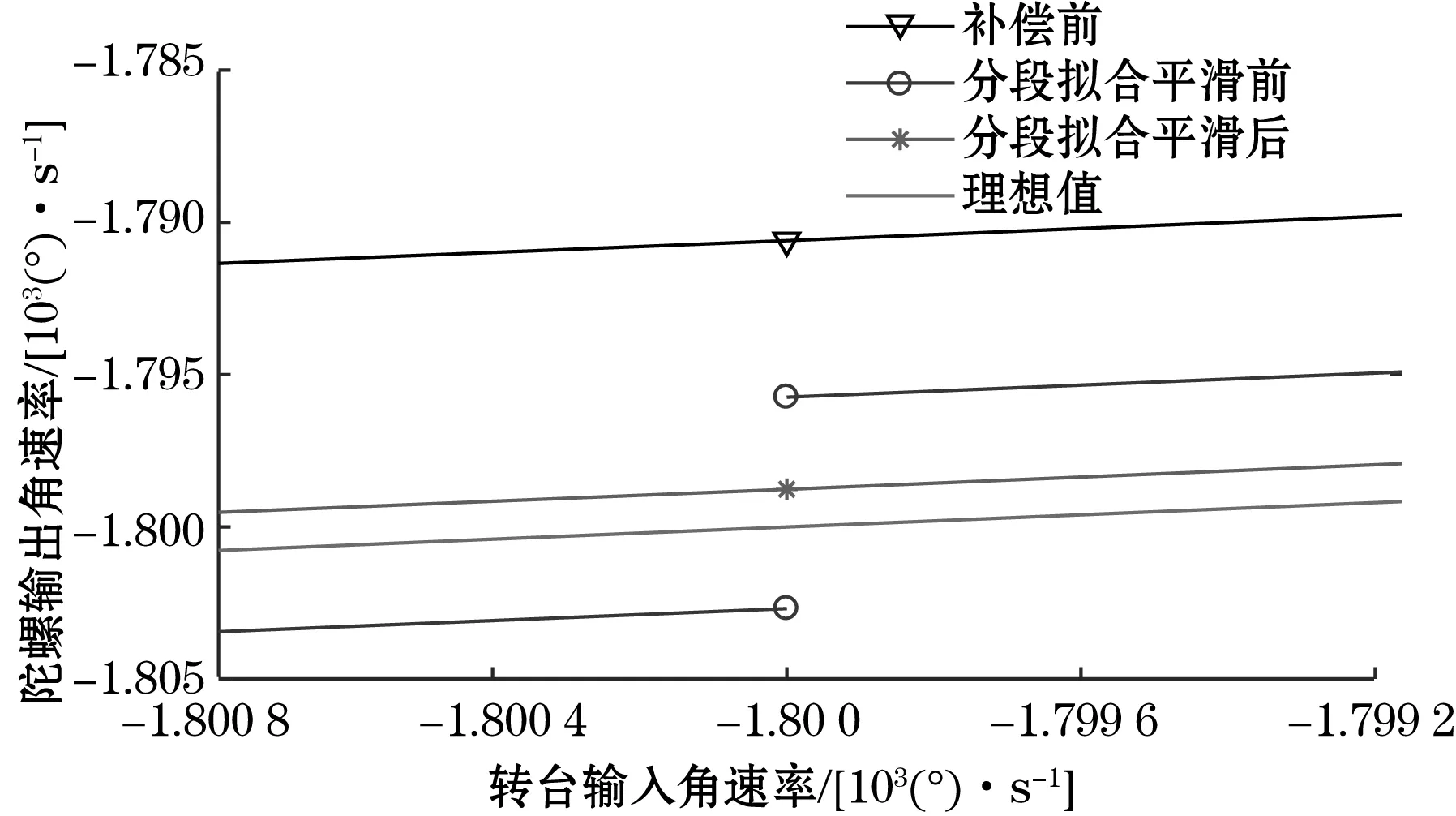
图4 分段拟合连续性对比

该方法使MEMS陀螺标度因数非线性误差提高了2个数量级，达到0.14%，耗时0.247 ms。为了更直观地对比3种方法的补偿能力，从全量程数据的补偿值及误差值两方面进行对比，3种补偿方法的结果如下。

由图5所示，通过3种不同的补偿方法，MEMS陀螺样机的原始输出均得到了有效的补偿，趋近于-3 600°/s至3 600°/s的理想线性输出。由图6可以看出分段回归拟合总体误差最小。3种方法的非线性误差指标可由式(5)和式(6)计算得到，如表3所示。

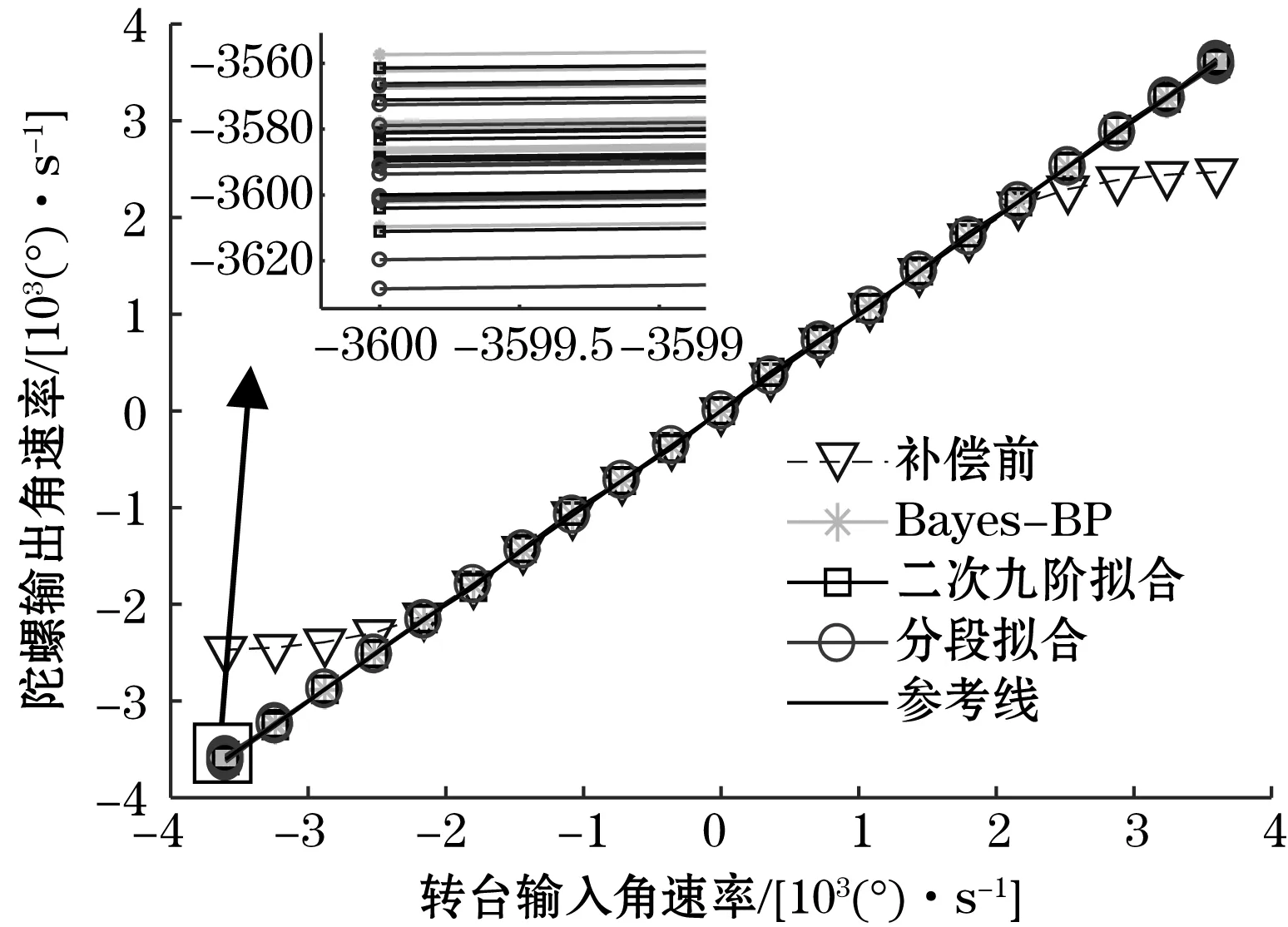
图5 MEMS陀螺样机在满量程下的输出(补偿前/后)

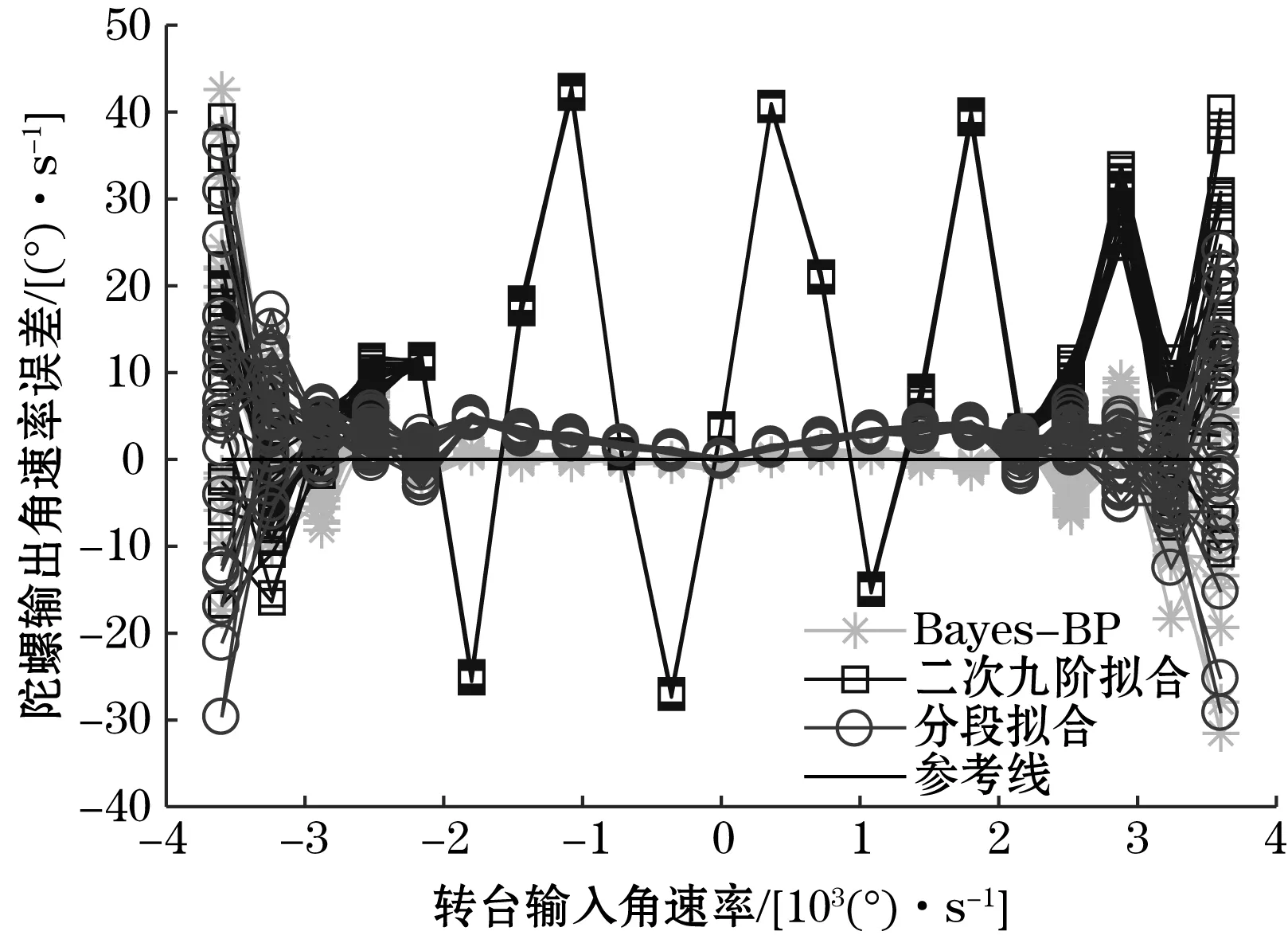
图6 标度因数非线性误差分析(补偿前/后)

从补偿后数据分析可知，启发式分段回归拟合方法补偿效果最佳，该方法使MEMS陀螺标度因数非线性误差降低了2个数量级，非线性误差降低到0.14%。Bayes-BP神经网络补偿曲线的结果优于多次高阶回归拟合曲线，但都逊于启发式分段多项式回归拟合。在处理时间上启发式分段多项式回归拟合方法运算速度为0.247 ms，运算速度是Bayes-BP神经网络的数十倍，是多次高阶多项式的2倍多。本文提出的启发式分段多项式回归拟合方法在保障MEMS陀螺样机输出精度的同时，保证了高动态测量环境下的实时性需求。

4 结论

MEMS陀螺标度因数随转速成强非线性变化，特别是在高转速输入区间,标度因数误差非线性尤其严重。针对此问题，本文探讨了MEMS陀螺样机的标度因数非线性误差的补偿方法，提出了启发式分段多项式回归拟合方法，通过多种曲线回归拟合补偿结果的对比分析，证明了其准确性和适用性。首先分析高转速下数据的非线性特点；其次通过启发式分段方法得出分段点，确定MEMS陀螺的线性区与非线性区；最后针对不同区域数据特点建立连续的回归拟合模型。该方法可减小MEMS陀螺标度因数非线性误差，提高其动态精度，具有一定的工程应用参考意义。