梁琦琦，冯红银萍

(山西大学 数学科学学院， 太原 030006)

在工程和物理学中，系统的耦合是普遍存在的。 在文献[1]中，作者讨论了ODE-热方程的耦合系统,证明了该耦合系统是指数稳定的。文献[2]研究了Euler-Bernoulli梁方程与热方程在边界耦合的系统,热方程作为整个耦合系统的控制器，使得耦合系统的解是指数稳定的。在文献[3-5]中，Zhang和Zuazua分别讨论了热方程和波方程在两类不同边界条件下的耦合，并证明了两种情况下的耦合系统是多项式稳定的。文献[6-7]研究了两个波方程的主方程耦合的系统，并且证明了在不同的假设条件下系统为指数稳定或一般稳定、本文研究了一类新的边界耦合的波方程系统，并证明了耦合系统是适定的、渐近稳定的但不是指数稳定的。

本文讨论如下的耦合波方程:

(1)

其中:k,c为正常数；wx或w′表示w对x的导数，wt表示w对t的导数。令:

φ(x,t)=u(1+x,t), 00

则上述系统等价于如下的耦合系统:

(2)

因此，只需考虑耦合系统(2)的适定性和稳定性。定义系统(2)的能量函数为:

对E(t)求导，并结合(2)得到:

因此E(t)是单调递减的。

将在如下状态空间上考虑系统(2)的适定性和稳定性：

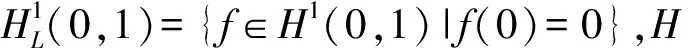
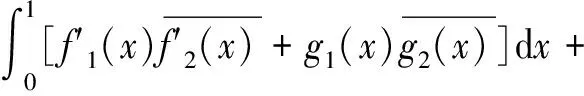
(3)

∀Xi=(fi,gi,hi,mi)∈H,i=1,2

定义算子Α:D(Α)(⊂H)→H为:

(4)

则系统(2)可以写成如下发展方程:

其中：X(x,t)=(w(·,t),wt(·,t),φ(·,t),φt(·,t))，X0(x)=(w0,w1,φ0,φ1)。

定理1 对任意初值(w0,w1,φ0,φ1)∈H，系统(2)有唯一的解使得(w(·,t),wt(·,t),φ(·,t),φt(·,t))∈C([0,∞);H)。此外，系统(2)的解是渐近稳定的，即:

(5)

证明算子Α由式(4)定义，则对任意的(f,g,h,m)∈D(Α)，简单计算可得:

Re〈Α(f,g,h,m),(f,g,h,m)〉=

cm(0)h(0)=-kg2(1)≤0

(6)

因此Α在H中耗散。对任意的(p,q,r,s)∈H，解方程Α(f,g,h,m)=(p,q,r,s)可得:

(7)

因此Α-1存在。根据Sobolev嵌入定理[8]，Α-1在H中是紧的。由Lumer-phillips定理[9]得：Α在H上生成C0-压缩半群。

接下来证明系统(2)是渐近稳定的。根据文献[10]可知：只要证明算子Α在虚轴上无特征值即可。事实上，假设

Α(f,g,h,m)=iz(f,g,h,m),(f,g,h,m)∈D(Α)

其中z∈R，可以得到(f,g,h,m)满足如下的方程组:

(8)

如果z=0,则f=g=h=m=0。现在假设z≠0,在式(8)前两个等式两边分别与f,h做内积,可得:

(9)

另一方面，利用分部积分公式，有:

(10)

比较式(9)和(10)可知:

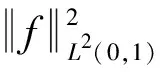
(11)

化简可得:

(12)

比较式(12)等号两边的虚部可知-izk|f(1)|2=0,由于k≠0,z≠0，故f(1)=0。由式(8)得(f,h)的解:

(13)

其中系数c1、c2、c3、c4满足如下的齐次线性方程组:

(14)

要使得方程组(13)只有零解，当且仅当方程组(14)的系数矩阵的秩为4， 即系数矩阵中有一个四级子式不为0。上述方程组的系数矩阵为:

它的四级子式分别为：

4isinz(zsinz-ccosz)

4isinz

4sinz(csinz+zcosz)

4cosz(zsinz-ccosz)

4(zsinz-ccosz)

若sinz≠0，则|A2|≠0,结论成立；若sinz=0，则cosz≠0，于是|A4|≠0，故方程组只有零解。表明Α在虚轴上没有谱，所以eΑt是渐近稳定的。

注记1 若Α为由式(4)定义的算子，则eΑt不是指数稳定。

事实上，对任意的λ∈σ(Α)，解Sturm-Liouville问题:

Α(f,g,h,m)=λ(f,g,h,m),(f,g,h,m)∈D(Α)

(15)

与定理1的第二部分证明类似，f,h式中的系数满足如下条件：

(16)

如果上述方程组有非零解，当且仅当系数矩阵的行列式值为零，即:

(c+λ)(k+2)e2λ+(2-k)(c-λ)e-2λ-2kλ=0

这就等价于:

(17)

只考虑下面1种情况:

(18)

根据Rouche定理[11]，得到如下的渐近表达:

λ=λn=nπi+O(n-1),n→∞

(19)

将式(19)代入式(18)，可以得到O(n-1)所满足的条件为:

(20)

结合式(19)，可得:

(21)

这里n是整数。由此可得系统(2)不是指数稳定的。