●

(萧山区第五高级中学,浙江 杭州 311202)

2016年3月，教育部《中国学生发展核心素养(征求意见稿)》出台，从文化基础、自主发展和社会参与三大方面提出了中国学生核心素养发展目标，而后各学科核心素养陆续提出.随着《普通高中数学课程标准(2017年版)》的颁布，明确提出数学核心素养包含数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析，这6个数学核心素养力图从根本上体现数学学科的育人价值.

数学运算是数学活动的基本形式，也是演绎推理的一种形式，是得到数学结果的重要手段.数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的过程.主要包括：理解运算对象、掌握运算法则、探究运算方向、选择运算方法、设计运算程序、求得运算结果等.数学运算，在任何时期的数学育人目标中都占有重要地位，它有助于我们借助运算方法解决实际问题；有助于促进数学思维发展，养成程序化思考问题的习惯；有助于形成一丝不苟、严谨求实的科学精神.

数学运算如此重要，但一线教师在教学中对其理解和教授似乎也存在诸多问题，诸如：1)理解运算概念狭隘——提到运算，很多教师立马联想到的是解析几何里繁杂的计算等；2)运算教学结构不清晰——因为对运算概念的理解不深刻，所以在面临运算教学时，运算教学开展脉络模糊；3)缺少提高运算素养的办法——如何能促进学生运算素养的提升，很多教师缺乏足够的理论认识，也缺少长久的有效机制建构办法，等等.如此，很多学生对“数学运算”的理解也往往只停留在“计算”的认识层面，不了解诸多丰富的运算概念、不知晓运算的建构、缺乏运算有效应用的品质等.针对上述问题，笔者试图谈谈运算的理解与如何从理解的角度开展运算教学.

1 数学运算的概念

数学运算，在数学上是一种程序性行为，按照一定的逻辑建立起一定的规则，实现已知量到新建量之间的对应关系，其本质是集合之间的映射.一般而言，数学运算指代数运算，在高中学习阶段，特别指二元运算和一元运算，其中二元运算指由两个元素形成第三个元素的一种规则，一元运算指通过特殊“算子”实现元素到元素的对应，如绝对值、积分等.

数学运算本质反映的是集合之间元素的对应关系，如对于集合S中的一对按次序取出的元素a,b，集合S中有唯一确定的第三个元素c和它们对应，叫做集合S中定义了一种二元运算.例如，算术中的加法1+2=3，这里1和2是输入，3是结果，而“+”表明这是一个加法运算，这便是一个常见的二元运算，本质上是A×B→C形式的映射，这里的S可以为有理数集Q、实数集R等.当然，有时也可以是从集合S依次取出a,b，对应另一个集合T中的元素c，如平面向量数量积的运算，正是从平面向量集合中任取两个向量a,b，对应于实数集中的元素c，即有a·b=c.

2 运算素养与其他素养的关系

高中数学核心素养包含6个方面：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据统计.不同核心素养在内涵和外延上具有独立性，在逻辑上构成一个有机整体，在教学中，这些核心素养不是孤立的，它们是紧密相关的.我们自然会思考：数学运算与其他核心素养存在怎样的关系？数学运算本身反映的是集合之间元素的对应关系，但从其建构、表征、操作、应用等方面可找到它与其他核心素养的联系(如图1所示)，通过数学抽象实现数学运算概念体系的建构，通过直观想象等方式实现数学运算的多元表征，通过逻辑推理实现数学运算的过程操作，最后实现数学运算到建模和统计等方面的应用.这也体现了当以数学运算为研究中心时，其他素养与它之间的关联结构，对于我们更好地开展数学运算教学也有十分重要的启示.

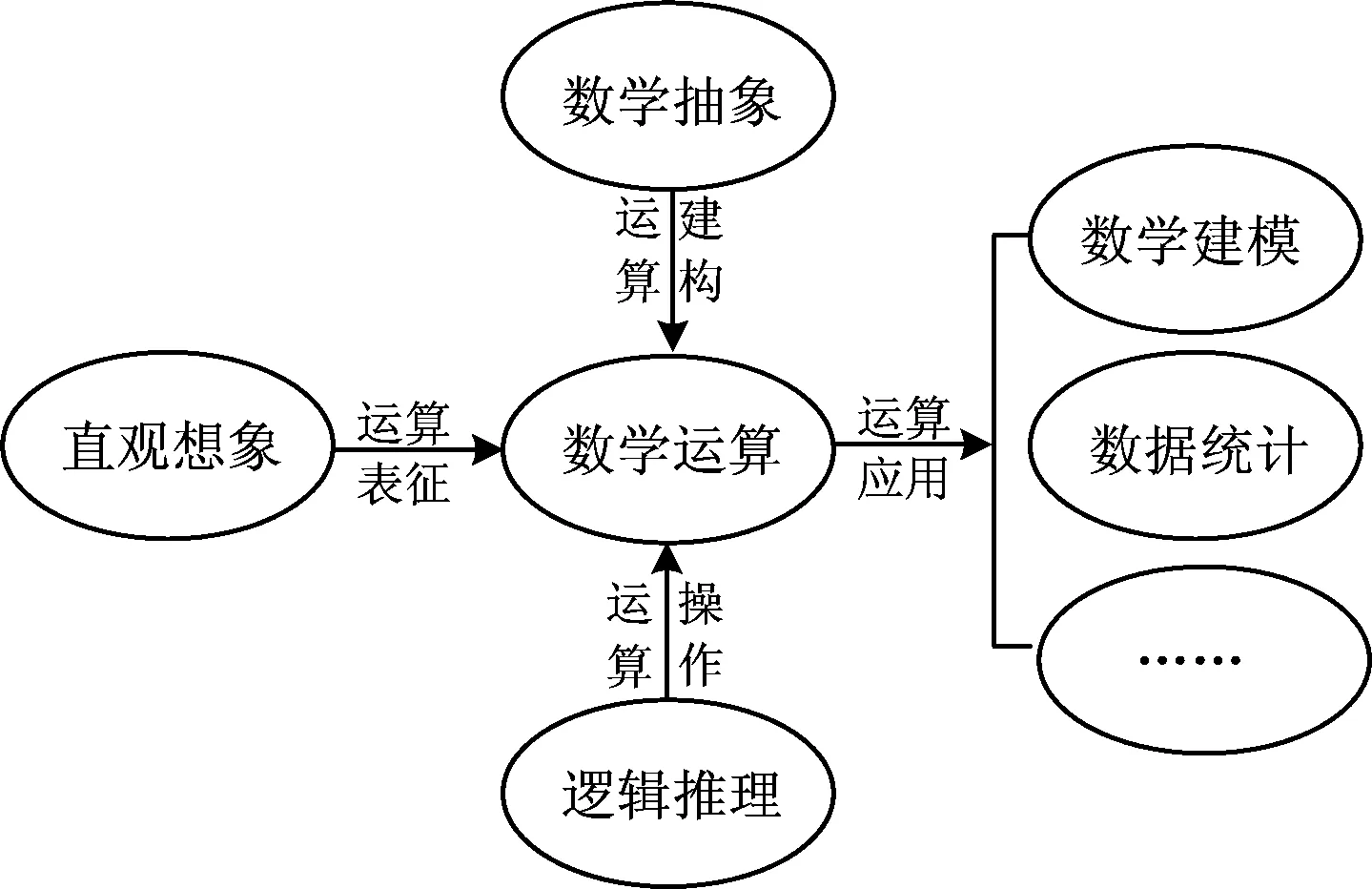
图1

3 数学运算的机制

“数学运算”包含算理、算法、算力.“算理”是运算的道理，即解决为什么能这样算的问题；“算法”是运算的方法，即解决怎样算的问题；“算力”是指开展运算的能力，即具体落实运算的过程，实现运算目标.他们相辅相成，构成一个运算的整体.在实际中，完成一项运算包含4个方面：理解运算意义、构建运算框架、实施运算过程、检验运算结果.

3.1 理解运算意义

理解运算意义，指理解运算提出的背景、运算的建构、运算的构成和运算的应用等.运算一定意义上实现的是问题解决，即利用已知量探索未知量，通过运算架起两者联系.而要利用运算解决问题，首先是要正确理解运算的意义.正如，当我们在运用空间向量数量积解决立体几何中的夹角与距离问题时，必须建立在对空间向量数量积理解的基础之上，知晓数量积运算的一系列运算法则，方此才能有效应用.

3.2 构建运算框架

构建运算框架，指的是对题意的分析，特别是分析已知与未知的关系，通过转化化归等方法大致构建问题解决的路径，以及大致列举需要构建的等式或不等式等.它是解题构思的过程，是解题者心中的一幅解题蓝图，为进一步的运算作好铺垫.

3.3 实施运算过程

实施运算过程，指的是建立运算框架之后开展的运算操作，它是对运算框架的细化和实施，也是运算过程的核心.利用条件构建等式或不等式，或由已知走向未知，步步逼近，或执果索因，逆向分析推导.运算，既是一项内在的思维活动，又是一项外在的思维表达行为，思维基于对运算概念的理解，运用运算的规则体系，实现运算的逻辑推理，又以数学语言的方式通过书写表达出来，故正确的推理与正确的表达是实现正确运算的必要条件.

3.4 检验运算结果

检验运算结果，指的是对运算结果的检查与反思，一方面我们要考虑是否漏解或多解，另一方面可以考虑将值代入检验是否符合题意.这也是在考查解题者的思维品质是否完备，在检验中如果代入成立，那么答案正确的可能性就极高，反之说明计算存在问题.检验意味着对运算结果的修正，也体现了解题者思维的缜密性.

4 数学运算的理解教学

4.1 理解数学运算的概念

概念是思维的细胞，概念是逻辑推理的基础.数学思维活动以概念为基础，运用概念间的关系进行推理.数学运算的理解教学，首先是要帮助学生理解概念本质.只有理解运算所表达的意义，才能有效建构运算法则，有效开展运算应用，因此理解运算概念是运算应用的基础.比如，在“对数”概念建构中，笔者正是抓住“对数到底表达了什么”这一核心问题开展教学.

4.2 理解数学运算的对象

要正确理解运算，其次是要帮助学生正确理解运算对象.对高中生而言，运算的认知起点是以实数为对象的运算体系，我们以此为中心尝试建构高中数学运算对象体系.比如指数运算、对数运算等，便是作为两类特殊的实数形式存在的运算关系；而随着系数的扩充发展，我们会学习复数及其运算；进一步，我们将角扩展到任意角且引进弧度制，使角和实数实现一一对应，从而发展到实数的三角运算问题；同时，平面(空间)几何，通过坐标法实现平面(空间)中点的坐标表示，将几何问题转化为实数运算问题，即我们常说的解析几何问题；同样，平面(空间)向量也可通过坐标表示，实现向量运算的坐标形式，即转化为实数运算.从这个角度看，高中阶段的运算还是以实数运算为核心.并且，我们还丰富了研究对象，比如集合运算、命题运算、函数的极限、求导与积分运算等等.当然，数学运算对象还包括很多，通过图2笔者想说明的是运算教学要抓住核心概念、抓住运算对象之间的联系.

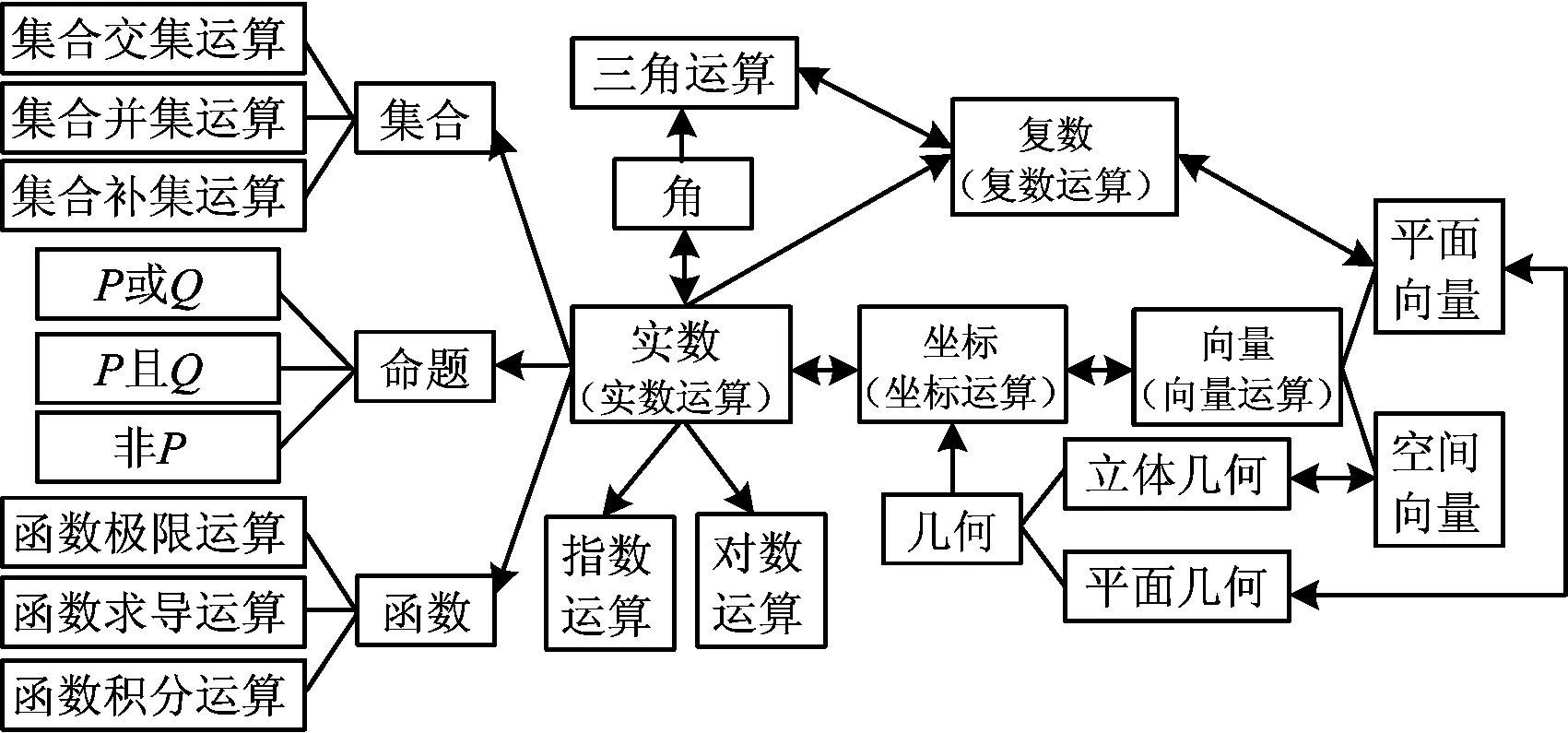
图2

4.3 理解数学运算的体系

一个运算，往往伴随着几个相关运算.如在我们常见的实数运算中，由加法引申出了它的逆运算——减法，并为了简化运算引申出了乘法，由乘法进一步引申出其逆运算——除法，等等.从本质上看，加法a+b=c是已知a，b得c的过程，而减法是已知a，c得b的过程，即有c-a=b，这便是一个互逆的过程.

一个运算，往往会研究其相关运算法则，因为相关的运算法则和运算律，能简化我们的运算，提升我们的运算速度，使运算有更多的方法和捷径可寻.一般地，运算律往往有交换律、结合律、分配律等.如在学习平面向量数量积运算后，我们会尝试探究平面向量数量积的交换律、数乘结合律，以及加乘分配律等，事实上，经过定义探索后有：a·b=b·a,λ(a·b)=(λa)·b,(a+b)·c=a·c+b·c,且一般地(a·b)·c≠a·(b·c)，而其证明既可以用数量积概念证明，也可借助数量积的几何意义证明.

学生学习数学是一个有指导的再创造过程，数学学习的本质是学生的再创造.数学运算的学习是有线索可以寻找的，是有一定逻辑的，我们要基于此培养学生这种数学直觉，教师应该关注学生建构运算的过程，努力挖掘创新点，给学生提供充分的再创造机会.数学运算学习的构建，也是培养学生系统思维的一个过程，因为一个运算总伴随着几个相关运算，一个运算往往会有相应的运算法则，系统思维的培养有助于学生正确理解数学运算，掌握数学运算的学习路径.

4.4 类比学习数学的运算

数学知识的学习，不是知识的简单堆砌，它是有联系、有逻辑的，教师需要帮助学生建立知识网络，形成结构清晰的知识图谱.而这其中重要的一点是要用数学方法把知识串起来、连成线、织成网.类比正是数学学习的一种重要方法，运用类比可以实现知识迁移学习.数学运算的学习也是如此，许多运算总是可以借助已有经验开展类比学习，融入“先行组织者”，同化新运算.

例如前面所说的对数学习，由“对数源出于指数”(瑞士数学家欧拉语)，课堂教学中，可以引导学生通过指数运算类比推导对数运算，为学生建构对数运算体系找到联结点.已知指数运算：2x·2y=2x+y，2x÷2y=2x-y，(2x)y=2xy,引导学生进行猜想和推导相应的对数运算.

由2x·2y=2x+y，设2x=M,2y=N，得

x=log2M,y=log2N,

且2x+y=MN,知

x+y=log2MN,

从而

x+y=log2M+log2N=log2MN,

一般地，logaM+logaN=logaMN.

同理，由2x÷2y=2x-y，设2x=M,2y=N，得

x=log2M,y=log2N,

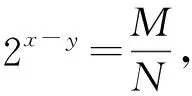
从而

再则，由(2x)y=2xy，设2x=M,得

x=log2M,

且My=2ylog2M,知

log2My=ylog2M,

一般地

logaMn=nlogaM.

4.5 理解数学运算的应用

数学的一个特点是具有广泛的应用性，而广泛应用的一个重要方面正是运算的广泛应用.这既体现了数学的应用价值，也体现了运算的应用价值.事实上，人们在建立一个运算时，最初的动机就是为了“有用”，为了解决一定的问题而建立相应的运算，再进行完善.因此，一个运算的建立，往往具有极强的应用价值.

如平面向量数量积在物理背景上即为力的做功问题，W=F·S=|F|·|S|cosθ.而这在数学学科看来是十分精妙的，数量积恰好将向量最重要的两个元素“长度”和“角度”融合在一起，使得数量积在数学应用中具有广泛的价值.

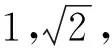
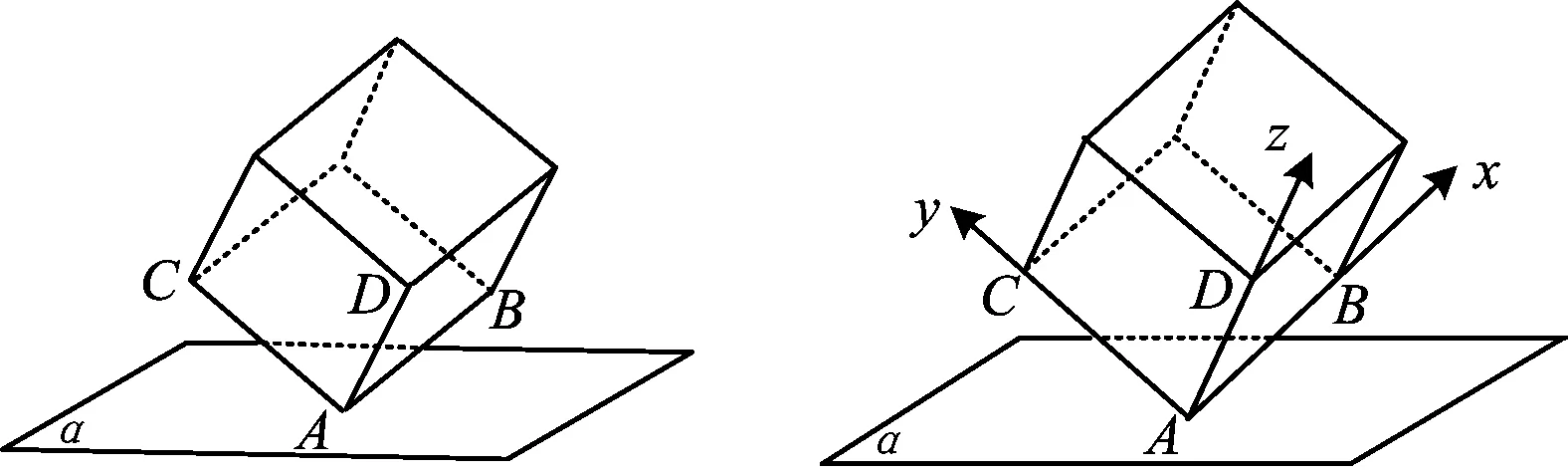
图3 图4

如图4建立空间直角坐标系，不妨设平面α的法向量为n=(x,y,z)，记点B,C,D到平面α的距离分别为h1,h2,h3，则

从而

故

运用向量运算实现了几何度量[1]，体现了数学运算的应用价值.

5 结束语

数学运算在数学育人目标中具有重要的地位和作用.本文从数学运算的概念、数学运算素养与其他素养的关联、数学运算的机制，以及数学运算的理解教学等方面开展了论述.数学核心素养的培养是一个长期的过程，需要教师在教学中持之以恒地渗透与培养；数学核心素养的培养是一项系统工程，是各个核心素养联动发展的过程，它们是一个有机整体.如今，当新的教育使命摆在我们面前时，作为一名数学教师一定要从培养“全面发展”的人的角度开展学科教学，真正体现学科教育在育人价值中的独特作用.