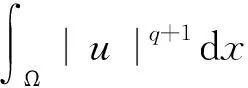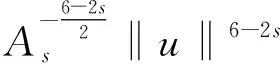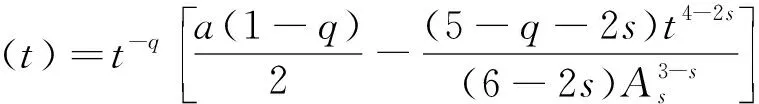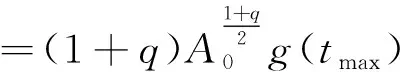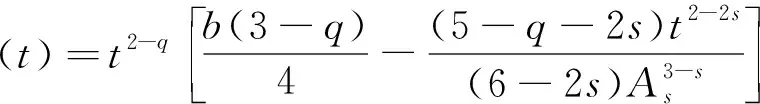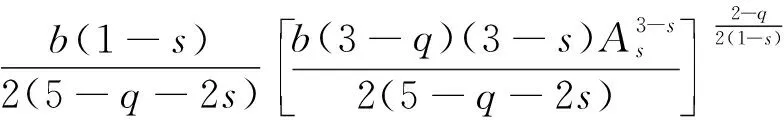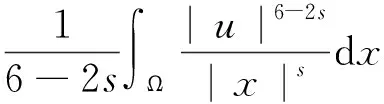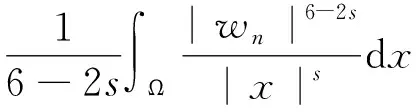一类带Hardy-Sobolev临界指数的Kirchhoff型方程正解的存在性*
2019-01-21李红英廖家锋
李红英,廖家锋,
(1 西华师范大学数学与信息学院, 四川 南充 637002; 2 遵义师范学院数学学院,贵州 遵义 563006)(2017年5月8日收稿; 2017年11月16日收修改稿)
考虑如下带Hardy-Sobolev临界指数的Kirchhoff型方程

(1)
2012年,Liu和Sun[1]研究如下问题

(2)
其中:4 一个自然的问题:问题(1)是否也存在正解?事实上,当s=0时,Sun和Liu在文献[4]中获得问题(1)正解的存在性,并提出一个公开问题:如何证明第2个正解的存在性?据查阅文献所知,这个开问题至今尚未解决。本文利用变分方法获得问题(1)的一个正局部极小解。在一定程度上,推广文献[1,4]的结果。 问题(1)对应的能量泛函为 记As为Hardy-Sobolev常数 (3) 特别地,当s=0, 首先,给出如下一个重要的引理。 引理1.1假设a,b≥0且a+b>0,0 (4) 证明由Hölder不等式和式(3),有 (5) (6) 从而,根据式(5)和式(6),可得 (7) 当a>0时,令 则 容易得到 使得 I(u)|u∈SR1≥ρ, (8) 则 容易得到, 使得 I(u)|u∈SR2≥ρ, (9) 故,当‖u‖充分小时,有 从而式(7)成立。引理1.1证毕。 下面,给出本文的主要结果及其证明。 证明根据引理1.1,只需证明存在u*∈BR(BR为引理1.1中所定义)使得I(u*)=m<0。由引理1.1的证明过程和式(1),可推得∀u∈BR有 ≥0, (10) 和 (11) 不失一般性,令wn=un-u*,由式(11)可推得 (12) ‖un‖2=‖wn‖2+‖u*‖2+o(1), (13) ‖un‖4=‖wn‖4+‖u*‖4+ 2‖wn‖2‖u*‖2+o(1), (14) 其中o(1)表示n→∞的无穷小量。再根据文献[6],可得 (15) 若u*=0,可得wn=un,这就意味着wn∈BR。若u*≠0,由式(13),当n充分大时有wn∈BR。从而,由式(10),可推得 (16) 故,由式(12)~式(16),有 这就意味着I(u*)=m<0且u*≢0,即u*能量泛函I的一个局部极小值点。因此,u*是问题(1)的非零解。由I(|u|)=I(u),不失一般性,可以假设u*≥0。根据强极大值原理,可得在Ω中u*>0。故,u*是问题(1)的正解且I(u*)<0。定理1.1证毕。 注记1.1一方面,将文献[1]中所研究的问题推广至带Hardy-Sobolev临界指数的情形,并获得问题(1)的正解的存在性;另一方面,当s=0时,定理1.1结果包含文献[4]的主要结果,而且我们的方法比文献[4]的方法简单。此外,定理1.1对于a=0,b>0或者a>0,b=0的情况同样成立。当a=0,b>0时,问题(1)被称为退化的Kirchhoff型方程;当a>0,b=0时,问题(1)退化为经典的奇异半线性椭圆方程。 注记1.2特别地,当a=1,b=0时,文献[7]研究问题(1)并获得2个正解的存在性。对于这类带Hardy-Sobolev临界指数的奇异椭圆方程的更多结果,可参见文献[7]的参考文献及其引用文献。这里提出一个公开问题:如何获得问题(1)的第2个正解?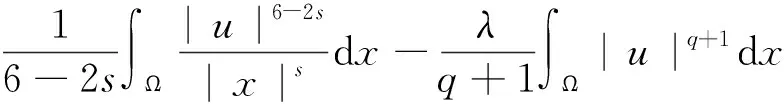
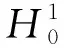

1 主要定理