唐润东

一、极化恒等式定义

极化恒等式的几何意义是：向量的数量积可以表示为以这组向量为邻边的平行四边形ABCD的“和对角线”与“差对角线”平方差的，即，其中M为对角线AC与BD交点.

二、基于定义的思考

在研究向量数量积的问题中，传统思路是将两点乘的向量进行分解（即一个向量转化为两个或两个以上向量之和），将不便于求的数量积化为多个可求的数量积“逐个击破”，或是建立平面直角坐标系用坐标法对要求的数量积进行代数运算来求得.而向量极化恒等式的出现，引起了笔者的注意，因为它用显而易见的平方差的方式巧妙地将数量积转化为两向量和的模平方减去两向量差的模平方，这是在常规题型中从未见过的转化方式.笔者进一步思考：这个向量极化恒等式怎么应用在解题中呢？在什么条件下应用向量的极化恒等式最为便捷和巧妙呢？

三、向量极化恒等式的应用

通过对大量向量数量积问题的研究，笔者发现向量极化恒等式在一类问题中有极高的应用价值：即当｜a+b｜或｜a-b｜中一个为定值时分析a·b的问题.下面我们通过几道例题体会向量的极化恒等式在研究该类问题时的优越性与便捷性.

例1若平面向量a，b满足｜2a-b｜＝3，求a·b的最小值.

若运用传统思路，为构造a·b的数量积形式，需将条件式两边平方后再对所得式应用基本不等式，再应用向量模与数量积的不等式求得最小值：

因为｜2a-b｜＝3，所以，得.

又4｜a｜2+｜b｜2≥4｜a｜｜b｜≥-4a·b，（当且仅当2a＝-b时等号成立），所以a·，即.

若将2a看作一个整体，｜2a-b｜＝3是定值，又a·b可看作，故本题完全符合“差对角线长为定值”的模型，在本题应用向量极化恒等式能大大简化步骤：

解（当且仅当2a＝-b时等号成立），所以.

例2已知在△ABC中，BC＝2，若对任意实数t，都有，t∈ R.求的最小值.

解设，因为t+（1-t）＝0，所以M，B，C三点共线.

接下来，若运用一般做法：以A为原点，方向为x轴正方向，建立平面直角坐标系，设B（x-2，-3），C（x，-3），x∈R，则，，故当x＝1时，.

图1

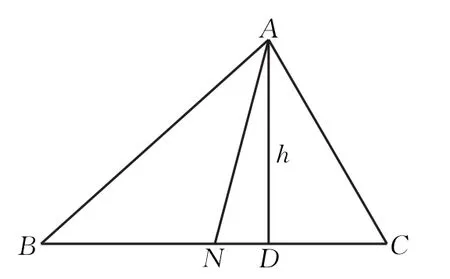
图2

取BC中点N，则

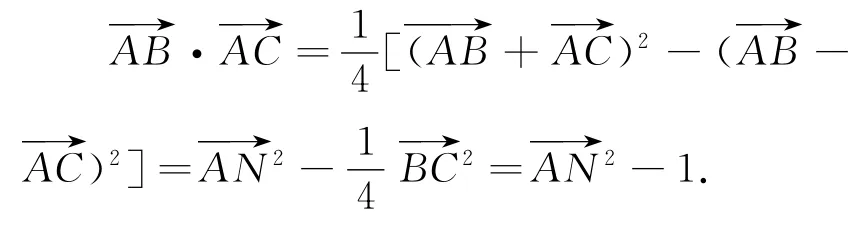
例3在Rt△ABC中，CA＝CB＝2，M，N分别为斜边AB上的两个动点，且，求的取值范围.

一般做法需建立坐标系，以C为原点，方向为x轴正方向，建立平面直角坐标系，则A（2，0），B（0，2），故直线AB：y＝2-x.

设M（x，2-x），N（x+1，1-x），（x∈[0，1]），则，

当x＝0或x＝1时，，所以.

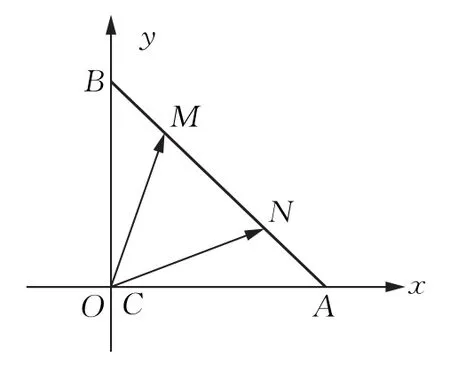
图3

取M N中点F，则F的极端位置是线段AB的四等分点，那么

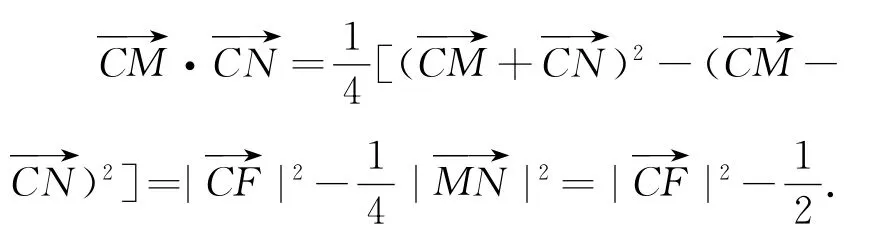
当F位于AB中点时，此时，；

当F位于AB四等分点时，，此时，，

点评当题目满足差对角线为定值时，利用向量极化恒等式可将研究数量积问题转为研究单一模长的问题，大幅度地将代数运算转化为简单的几何分析，大大简化解题过程.

例4设△ABC，P0是边AB上一定点，满足，且对于边AB上任一点P，恒有，则（ ）

A.∠ABC＝90° B.∠BAC＝90°

C.AB＝ACD.AC＝BC

解取BC中点M，则.

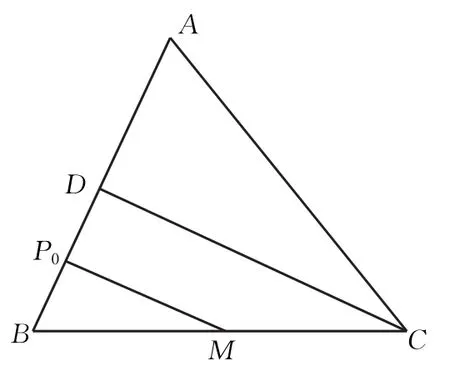
图4

过点C作CD⊥AB于点D，则CD∥P0M.又M为BC中点，所以P0为BD中点，所以，所以D为AB中点.

又CD⊥AB，所以CD为边AB的中垂线，因而AC＝BC，故选D.

点评在分析已知数量积最值问题中，利用向量极化恒等式，可将数量积的条件转化为模长条件，将代数分析变为几何分析，使分析过程变得便捷明了.