广东省广州市南海中学(510170) 沈钢

在教学任务重,数学课堂的常见教学模式是讲练结合,讲公式定理,讲例题,练习,再练习的教学方式,课堂容量大,课堂效果显著,但是课后学生掌握情况非常不好.不能很好的理解和归纳总结,没有时间思考问题的本质.因此学生的学业成绩也就不稳定,经过多次的教研活动,听取了好多有经验的一线教师的讲座,有很多是讲变式教学,创新教学,以及讲题时的一题多解,归纳出多解归一的本质教学方式.下面我谈谈我在教学中运用“一题多解”的一些体会.

一、一题多解有利于培养学生的思维的广阔性

例1(广州市高二数学竞赛题)f(x)=x4=a0+a1(1-x)+a2(1-x)2+a3(1-x)3+a4(1-x)4,求a3的值.

解法一平移变换

因为f(x)=x4=a0+a1(1-x)+a2(1-x)2+a3(1-x)3+a4(1-x)4①,将f(x)向左平移一个单位,所以f(x+1)=(x+1)4=a0-a1x+a2x2-a3x3+a4x4②.在第②式中,x3的系数为-a3,而(x+1)4的x3的系数为C14=4,故-a3=4即a3=-4.

点评此解法通过函数图形的平移,将右边巧妙地将1-x转化为x,由烦到简.同时将左边转为(1+x)4成为二项式定理的常见形式.此解法,培养了学生从函数平移的角度思考,更加理解函数平移后函数值的不变,以及二项式定理中系数得概念,加深理解了二项式定理.

解法二构造条件

f(x)=x4=(-x)4=(1-x-1)4=[(1-x)-1]4,利用二项式定理展开,即求a3是 (1-x)3的系数,即C34(-1)1=-4,所以a3=-4.

思路总结由于题目中把(1-x)看成一个整体,于是就拼凑出一个新的二项式(a+b)4,使其中b=1-x,那么展开式形如下列形式,与题目已知条件符合.a0+a1(1-x)+a2(1-x)2+a3(1-x)3+a4(1-x)4.

解法三由条件构造新思路

f(x)=x4=[1-(1-x)]4,利用二项式定理展开,即求a3(1-x)3=C34[-(1-x)]3=-4(1-x)3,所以a3=-4.

点评此解法与解法二几乎相同,只是在变形时负号的处理不一样.

解法四换元代换

令1-x=t,则x=1-t,所以f(x)=x4=(1-t)4=a0+a1t+a2t2+a3t3+a4t4.要求a3即求t3的系数:C34(-t)3=-4t3,所以a3=-4.

点评解法四与解法二,三本质都是一样的,都是拼凑出题目条件(1-x)的形式.从题目已知条件整体看待的思想.拓阔了学生的数学思维,培养学生从不同角度去思考问题.以上四种解法其实都是一个知识点,就是利用二项式定理展开式系数的性质.虽然是一题多解,实际是多解归一,即都是利用二项式定理的性质.但是以上解法是从不同角度变形后再利用二项式定理,加深了学生对二项式定理如何灵活展开运用.

解法五利用求导函数

f′(x)=4x3=-a1-2a2(1-x)-3a3(1-x)2-4a4(1-x)3,f′′(x)=12x2=2a2+6a3(1-x)+12a4(1-x)2,f′′′(x)=24x=-6a3-24a4(1-x),f′′′(1)=24=-6a3-24a4(1-1)=-6a3,所以a4=-4.

点评从函数的调度出发,右边f(1)=a0,求导一次后带入x=1的值右边等于-a1,依次继续求导,再代入x=1依次可求出a2,a3,a4的值.这里不需要引入多阶导数,让学生理解求一次导f(x)就会降幂一次,一元三次函数是高中常见的利用导数求解的函数压轴题,因为一元三次求导后降幂为一元二次函数,而一元二次函数是初高中常见的基本初等函数.从而加深学生对函数与导数的联系的理解.

通过上面例题的几种解法,学生不但清晰的理解了二项式定理展开式的运用,而且也会从函数的角度去思考问题,有利于培养学生的发散思维能力和解题技巧,拓宽了学生思维的广阔性,加深对知识内在联系,因此更好的理解知识.

为了让学生更好的理解和掌握此题的解题方法和突破本题的关键点,下面给出一组变式题.

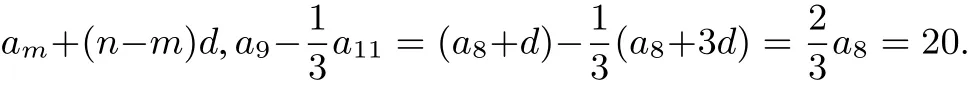
点评充分利用了等差数列任意两项之间的关系,把a9和a11都转为与a8的联系.

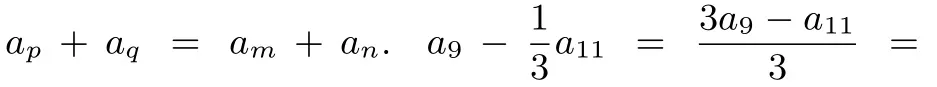
点评利用两次性质巧妙转化.培养了学生从更高角度去审题,组合整体看待的思维方式.

点评此性质教科书没有要求,但是通过这题的利用推广性质,开阔了学生的视野,激发了学生探索新规律的欲望,这个性质是否可以拓展到4个,5个,n个呢?让学生养成了勤于思考,勇于探索新知,大胆去猜想尝试.提高了学生解决问题的思维能力.

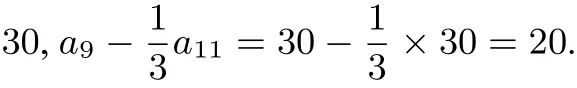
点评对于选择填空题是一种不错的解题技巧.大胆利用特殊值或特殊情况去解决不需要解题过程的题型.

教学实践证明:一题多解对对培养学生的联想能力、引起多向思维都是十分有益的,也是从根本上提高学生业绩行之有效的方法.