荀 立, 崔世崇, 朵 兰

(长春工业大学 数学与统计学院, 长春 130012)

左截断右删失(LTRC)数据在生物医学、 工程寿命试验、 劳动力经济和保险精算等领域应用广泛. 对于这类数据, 由于观测到的数据不完全, 因此一般采用乘积限方法估计感兴趣变量的分布函数. 分布函数乘积限估计的反函数, 称为乘积限分位函数. 两个分位数的差称为分位数差, 分位数差也可表示感兴趣分布的离散程度, 比标准差更稳健. 对于中位数对称的两个分位数差, 可以用来分析感兴趣分布的对称程度.

在右删失数据下, 文献[1]基于Kaplan-Meier乘积限研究了分位数差的估计及其渐近性质； 文献[2]利用光滑经验似然方法得到了分位数差的置信区间. 对于LTRC数据, 文献[3-4]讨论了分位剩余寿命的差和比的统计推断问题; 文献[5]基于Tsai-Jewell-Wang(TJW)乘积限, 研究了分位数差的估计及其大样本性质; 文献[6]进一步计算了分位数差估计的强收敛速度和均方收敛速度. 由于TJW乘积限估计是阶梯函数, 因此对应的乘积限分位函数也是阶梯函数. 如果总体分位函数连续, 则用连续函数估计连续的总体分位函数更易表达感兴趣变量的性质. 因此, 文献[7]通过对乘积限分位函数进行光滑处理, 提出了光滑分位函数.

本文通过对文献[7]的光滑分位函数做差, 得到总体分位数差的一个光滑估计, 利用经验过程的相关理论, 研究光滑分位数差估计的相合性、 渐近正态性等大样本性质. 进一步, 在均方误差的意义下, 与TJW 乘积限分位函数的差进行比较. 数值模拟结果表明: 在均方误差意义下, 当窗宽的取值低于0.05或高于0.25时, 根均方误差比出现负值, 即此时的光滑估计没有统计优越性； 当窗宽在0.05～0.25内取值时, 光滑分位数差的估计效率比乘积限分位数差的估计效率高, 但光滑分位数差牺牲了估计的无偏性, 而且由于核函数的性质, 光滑分位数差估计仍是总体分位数差的渐近无偏估计.

1 预备知识

其中Z(n)=max{Z1,…,Zn}.

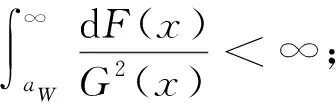
(H2)k(·)是[-1,1]上的概率密度函数, 对于整数r≥2, 有

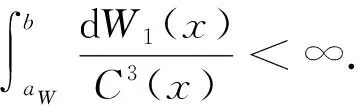
例1设F(x)=1-e-x,H(x)=1-e-x,G(x)=1-e-2x,k(x)=I[-1,1](x)/2, 则有:

1)W(x)=1-e-2x,aG=aW>0,bG=bW=∞, 进而有e-aW<1. 由于(1-y2)-2在[0,e-aW]上是连续、 有界、 单调递增的函数, 所以

2)k(x)为[-1,1]上的概率密度函数, 且r=2.

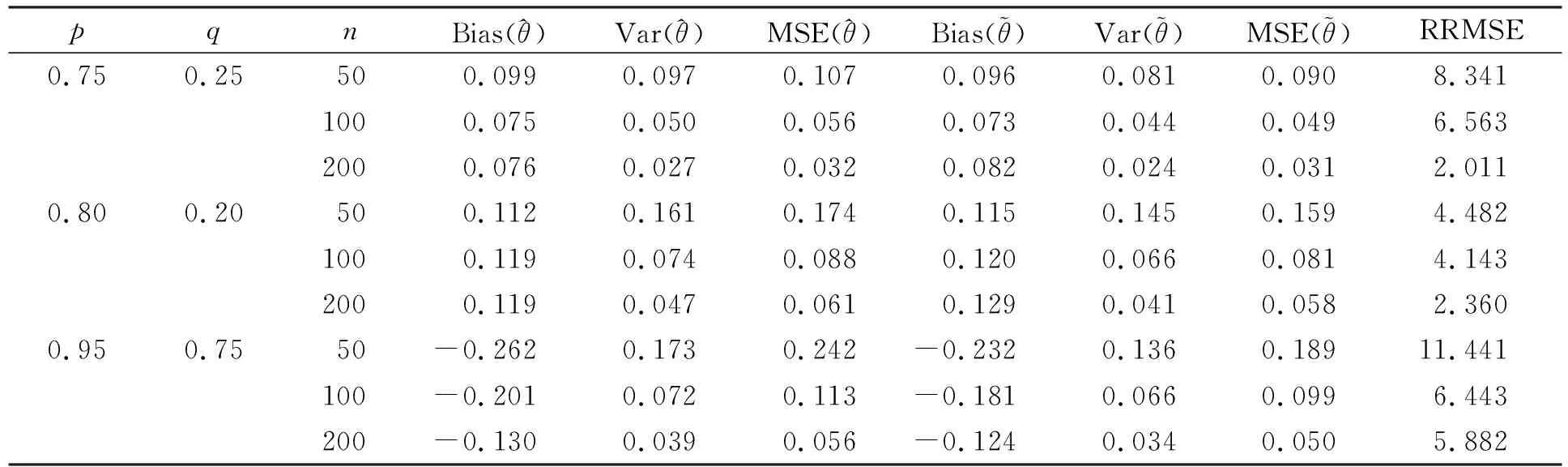
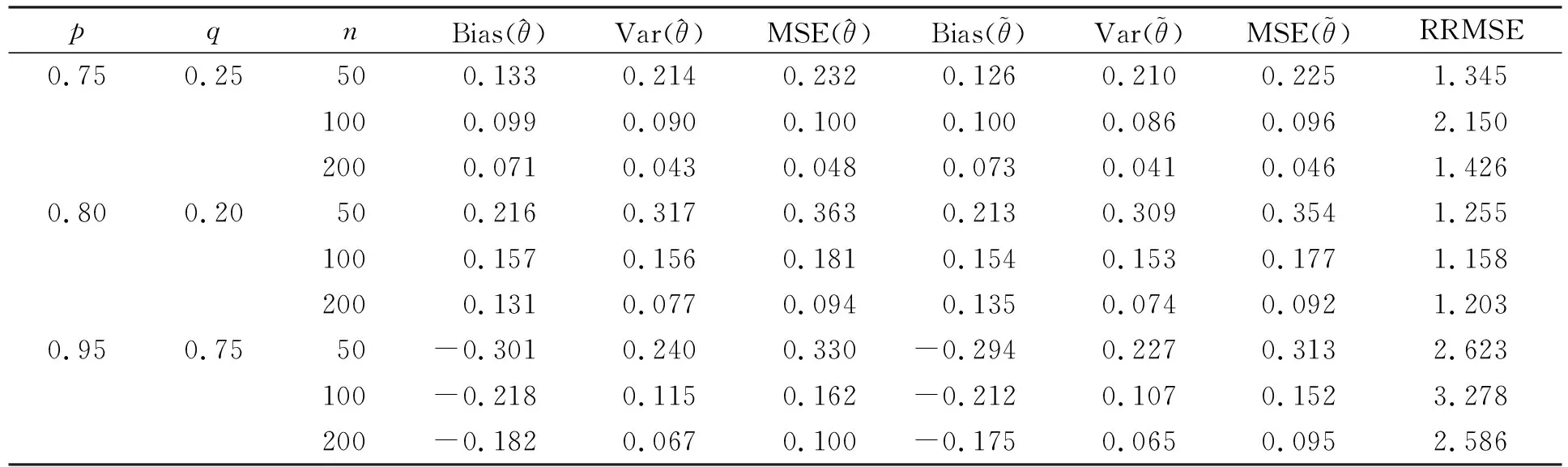
命题1[9-10]若aG≤aW, 对某些b

其中:

2) 对λ>0,ε>0,C(z)≥ε及某个常数K, 有

命题2[11]∀ε>0,F在[Q(p1)-ε,Q(p2)+ε]上两次连续可导, 0

2 主要结果

(1)

证明: 由命题2, 有

由命题1及文献[10]中推论2.2知,

因为f(Q(p))>0和f(Q(q))>0, 所以

对某个ξ1,ξ2: 0≤ξ1,ξ2≤1, 有

其中Q(r)(·)为Q(·)的r阶导函数. 由条件(H2), 有

其中

(2)

因为

由条件(H2)和中心极限定理, 有

其中式(2)成立. 由定理1的证明, 有

从而结论得证.

其中:kf(·)为一个核函数; {an}n≥1是一个正的窗宽列, 当n→∞时, 有an→0,nan→∞.

3 数值模拟与分析

情形1) 50%删失率和50%截断率, 其中F(x)=1-e-x,H(x)=1-e-x,G(x)=1-e-2x;

情形2) 30%删失率和25%截断率, 其中F(x)=1-e-x,H(x)=1-e-3x/7,G(x)=1-e-30x/7.

选用高斯核函数, 窗宽列为hn=…,0.05,0.08,0.10,0.12,0.15,0.18,0.20,0.22,0.25,…, 水平(p,q)=(0.75,0.25),(0.80,0.20),(0.95,0.75), 样本容量n=50,100,200, 重复模拟500次, 计算两个分位数差估计的根均方误差比

其中估计的偏差、 方差和均方误差分别记为Bias(·),Var(·)和MSE(·). 从偏差、 方差和均方误差三方面比较两个估计的效率, 其中根均方误差比表示均方误差意义下光滑估计提高的效率. 在上述两种不同删失率和截断率下, 窗宽分别为hn=0.05,0.15,0.25的数值模拟结果分别列于表1～表6.

表1 删失率为50%、 截断率为50%、 窗宽为0.25的数值模拟结果

表2 删失率为30%、 截断率为25%、 窗宽为0.25的数值模拟结果

表3 删失率为50%、 截断率为50%、 窗宽为0.15的数值模拟结果

由表1可见： 两个估计的偏差、 方差和均方误差几乎都随样本容量的增大而减小; 光滑估计的偏差普遍大于乘积限分位数差估计的偏差, 因为光滑方法牺牲了估计的无偏性; 但光滑估计是渐近无偏的； 光滑分位数差估计的方差和均方误差都比乘积限分位数差估计值小, 表明此时在方差和均方误差意义下, 光滑方法提高了估计效率; 根均方误差比表示估计效率提高的比值, 例如, 样本容量为50的四分位差θ(0.75,0.25)的两个估计, 光滑方法将估计效率提高了1.609%, 对于更大的分位数差θ(0.80,0.20)和尾部分位数差θ(0.95,0.75)也有类似结果. 表2中分位数差θ(0.80,0.20)的两个估计的根均方误差比出现负值, 表明此时乘积限分位数差估计比光滑分位数差估计更有效, 光滑方法不具有统计优越性. 表4的删失率和截断率与表3不同, 但得到了与表3类似的结果, 表明在适当选择的窗宽下, 不同的删失率和截断率对估计效率的提高无影响. 表5的结果类似表1, 对于删失率为50%、 截断率为50%、 窗宽为0.05的情形, 仍然有光滑分位数差估计的效率高于乘积限分位数差估计的结果. 表6的结果类似表2, 表明窗宽为0.05时, 光滑分位数差的估计效率并不比乘积限分位数差估计的效率高.

表4 删失率为30%、 截断率为25%、 窗宽为0.15的数值模拟结果

表5 删失率为50%、 截断率为50%、 窗宽为0.05的数值模拟结果

表6 删失率为30%、 截断率为25%、 窗宽为0.05的数值模拟结果

上述结果表明: 窗宽高于0.25或低于0.05时, 根均方误差比出现负值, 此时光滑分位数差没有统计优越性; 当窗宽在0.05～0.25内取值时, 根均方误差比大于0, 说明此时光滑分位数差估计比乘积限分位数差估计具有更高的效率.

注1本文根据文献[7]的光滑分位函数定义总体分位数差的估计量, 并与文献[5]定义的乘积限分位数差估计比较估计效率, 所有理论证明均在截断变量、 寿命变量、 删失变量相互独立的条件下进行.

对于寿命变量与删失变量相依的情形, 根据文献[12], 产生长度偏差右删失(LBRC)数据, 考虑LBRC数据下样本分位数差的估计. 用本文方法, 在均方误差意义下, 选择适当的窗宽, 得到类似估计效率的改善结果列于表7～表11.

表7 删失率为50%的LBRC数据下窗宽为0.25的数值模拟结果

表8 删失率为30%的LBRC数据下窗宽为0.25的数值模拟结果

表9 删失率为50%的LBRC数据下窗宽为0.15的数值模拟结果

表10 删失率为30%的LBRC数据下窗宽为0.15的数值模拟结果

表11 删失率为50%的LBRC数据下窗宽为0.05的数值模拟结果