一类离散不确定切换系统的滑模控制
2018-08-21刘永慧苏庆堂韩美杰
刘永慧, 苏庆堂, 韩美杰
(1.上海电机学院 电气学院, 上海 201306;2.鲁东大学 信息与电气工程学院, 山东 烟台 264025)
在过去的20年中,切换系统作为一类特殊的混合动态系统一直备受关注。这主要是由于很多实际工程系统,如航空航天控制系统、化工过程控制和网络控制系统等,都可以用这类系统进行描述[1]。此外,切换信号的存在使得切换系统动态性能变得更复杂。切换系统有一个典型特征,即当所有的子模态均稳定时切换系统不一定满足稳定。因此,切换系统的稳定性分析和镇定问题得到了学者们的广泛关注[2-5]。
随着计算机技术的迅猛发展,基于离散采样的数字控制器被广泛应用,因此很多经典的控制方法被推广到离散系统。近年来,关于离散切换的稳定性分析和镇定问题的研究也得到了很多重要结论[6-8]。其中,文献[6]在子系统均稳定的情况下采用平均驻留时间方法研究了离散线性切换系统的定性。之后,这一结论又被进一步推广到文献[7],文中考虑的切换系统不再约束每个子系统满足稳定。在此基础上,Zhai[8]进一步讨论了当子系统均不稳定时离散切换系统的状态反馈和输出反馈控制。
众所周知,滑模控制是一种有效的鲁棒控制方法,它具有快速响应、对不确定参数和外界扰动有强鲁棒性等优良特性。因此,滑模控制方法被广泛应用于离散系统[9-10]、随机系统[11-12]和马尔科夫切换系统[13-14]中。近年来,切换系统的滑模控制逐渐受到关注[15-18]。其中,Wu等[15]讨论了带有状态时滞的切换系统的滑模控制,这一结论又进一步被推广到随机切换系统[16]。此外,文献[17]研究了一类不确定切换系统的鲁棒H∞控制。上述文献中考虑的切换系统均是约束输入矩阵相同。笔者课题组近期在输入通道不同的情况下提出了一种输入矩阵加权方法,设计了一个公共滑模面[18],然而,关于离散切换系统的滑模控制未被考虑。这主要是由于离散滑模控制器设计中,系统离散采样导致系统状态轨迹不能一直维持在滑模面上滑动,而是在滑模面上不断地进行切换,从而形成准滑动模态,这给滑模控制器的设计带来了一定的困难。此外,由于切换系统动态性能的复杂性,已有的切换系统滑模控制的工作不能简单地推广到离散切换系统。
基于以上论述,本文将讨论一类不确定离散切换系统的滑模控制。与已有工作[15-17]相比较,本文不要求子系统具有相同的输入通道。首先,采用输入矩阵加权方法设计一个公共滑模面;接着,运用平均驻留时间方法研究了滑动模态的稳定性;最后,设计滑模控制律分析了准滑动模态的可达性。
符号:对于任意向量x∈Rn, ‖x‖表示欧式范数;Rm×n表示m×n维矩阵空间;对于任意对称矩阵M,M>0(<0)表示正定矩阵;I表示单位矩阵,向量ln∈Rn是由元素1组成的,ei∈Rn表示第i个基向量;⊗表示积克罗内克积;λmax(·)和λmin(·)表示对称矩阵的最大特征值和最小特征值;diag(·)表示对角矩阵;rank(·)表示矩阵的秩,矩阵中对称部分用*表示。
1 系统描述
考虑不确定离散切换系统如式(1)所示。
x(k+1)=(Aσ+ΔAσ(k))x(k)+
Bσ(u(k)+fσ(x(k)))
(1)
式中:x(k)∈Rn是系统状态;u(k)∈Rm是控制输入;Ασ和Bσ是已知矩阵;ΔAi(k)是不确定参数;fσ(x(k))是外部扰动;{Aσ,Bσ:σ∈Γ}是一组取决于指标集σ的分段常值函数,称作切换信号。
本文中假设不确定参数ΔAσ(k),则σ∈Γ满足
ΔAσ(k)=EσFσ(k)Nσ

此外,假设扰动fσ(x(k))范数有界,即
‖fσ(x(k))‖ 式中:dσ>0为已知参数。 为了便于推导,当σ(k)=i,i∈Γ时, 系统的参数简记为 Aσ=Ai,ΔAσ(k)=ΔAi,Bσ=Bi,fσ(x(k))=fi(k) 因此,对于σ(k)=i,系统(1)可以表示为 x(k+1)=(Ai+ΔAi)x(k)+Bi(u(k)+fi(k)) (2) 值得注意的是,本文不要求子系统的输入矩阵Bi∈Rn×m相同,这给设计共滑模面带来困难。为了克服这个困难,引入如下矩阵加权方法[18]: 式中:αi∈R为界参数,并满足 (3) 假设1:矩阵Bi列满秩,即rank(Bi)=m。 为了实现系统(1)的滑模控制,给出引理1。 引理1:令D,H和F(t)为适当维数的矩阵,且F(t)满足F(t)TF(t)≤I,则对于任意的参数ε>0,有下式成立。 DF(t)H+HTFT(t)DT≤ε-1DDT+εHTH 为便于后面的推导, 给出下面的定义。 定义1[19]:在滑模面S(k)=0的δ邻域内,如果下式成立: ‖S(k)‖≤δ 则称此滑动模态为准滑动模态。其中,参数δ>0定义为准滑动模态的带宽。 定义2[20]:对于任意的kv>ks>k0,令Nσ(k)(ks,kv)表示σ在区间[ks,kv]上的切换次数。如果下式成立: 则Nσ称作平均驻留时间,N0为初始的切换次数。不失一般性, 本文亦假设N0=0。 定义3:系统(1)的平衡点x*=0在切换信号σ(k)的作用下称作指数稳定,如果存在参数ρ>0, 0<β<1使得系统的解x(k)满足 ‖x(k)‖≤ρβ(k-k0)‖x(k0)‖, ∀k≥k0 本文考虑设计一个不依赖于模态的公共滑模面。公共滑模面设计为 S(k)=Dx(k) (4) 注3:如果设计依赖于模态的多滑模面,那么当状态轨迹在不同的模态间进行切换时滑模面的可达性分析将变得非常复杂,因此本文设计一种不依赖于模态的公共滑模面,有效地避免上述问题。 由离散系统的滑模控制理论可知,理想滑模面满足 S(k+1)=S(k)=0 (5) 由式(4)和(5)可得 D(Ai+ΔAi)x(k)+DBi(ui(k)+fi(k))=0 (6) 则等价控制ueq(k)为 ueq(k)=-(DBi)-1D(Ai+ΔAi)x(k)-fi(k) (7) 将式(7)代入系统(2)得到理想滑动模态为 x(k+1)=(I-Bi(DBi)-1D)(Ai+ΔAi)x(k) (8) 通过设计滑模面,得到了相应的理想滑动模态(8)。为分析滑动模态的指数稳定性,本文采用了平均驻留时间方法。 定理1考虑满足假设条件的系统(1),给定参数0<γ<1,如果存在矩阵Pi>0和参数εi1>0,εi2>0,i∈Γ,则线性矩阵不等式: (9) (10) 式中: 则对于参数 (11) 平均驻留时间Tσ满足 (12) 切换系统(8)指数稳定,并且系统的状态轨迹满足 ‖x(k)‖≤ρβk-k0‖x(k0)‖ (13) 式中: (14) 证明:对于切换系统(8),考虑第i个子系统的Lyapunov函数为 Vi(k)=xT(k)Pix(k) (15) 则由式(2)可得 (16) 由式(16)和 Schur’s补可知 Vi(k+1)-γVi(k)<0 (17) 可由 (18) 推导得到,其中 由引理1可知,式(18)可以重新表示为 (19) 由 Schur’s补可知,式(19)可由式(9)和(10)推导得到。 由式(17)可知 Vi(k+1)≤γVi(k) (20) 则对于任意的k∈[kl,kl+1],由式(20)可知 Vσ(k)(k)≤γ(k-kl)Vσ(kl)(kl) (21) 由式(11)和(21)可以推导得 Vσ(k)(k) ≤γ(k-kl)μVσ(kl-1)(kl) ⋮ ≤γ(k-k0)μ(k-k0)/TσVσ(k0)(k0) ≤(γμ1/Tσ)(k-k0)Vσ(k0)(k0) (22) 考虑到式(14),可得 a‖x(k)‖2≤Vσ(k)(k) (23) 且 Vσ(k0)(k0)≤b‖x(k0)‖2 (24) 由式(12)可知 αμ1/Tσ≤γμ-lnγ/lnμ≤1 (25) 结合式(22)~(25),可以得到 (26) 因此,理想滑动模态满足指数稳定。证毕。 为了保证准滑动模态的可达性,这一节将设计滑模控制器。为了实现控制目的,设计如下的基于指数型趋近律的滑模控制器。 S(k+1)-S(k)=-εTsgn(S(k))-qTS(k) (27) 式中:T为系统采样时间;ε和q为已知参数且满足0<ε<1和1-qT>0。 由式(8)和(27)可以得到滑模控制律为 u(k)=-(DBi)-1(DAi-(1-qT)D)x(k)- (28) 式中:Gi(k)=(DBi)-1DΔAix(k)+fi(k)。 由于控制器(29)中含有不确定项Gi(k),实际控制系统中无法实现。因此构造如下的滑模控制器: (29) 式中: (30) 式(30)中参数η>0。 接下来,本文将给出准滑动模态的可达性分析。 定理2考虑满足假设条件1的切换系统(1),设计滑模控制器(29),则准滑动模态区域 (31) 于有限时间内可达。此外,系统状态轨迹一旦进入该区域将始终在其内部滑动。 证明: 选择如下Lyapunov函数 V(k)=ST(k)S(k)。 (32) 由式(5)和滑模控制律(29)可得 (33) 由式(30)进一步得到 (34) (35) 结合式(34)~(36)可知 ΔV(k) =(1-qT)2ST(k)S(k)-2εT(1-qT)‖S(k)‖+(εT)2-ST(k)S(k)- 2ηi(1-qT)‖DBi‖‖S(k)‖+ηi‖DBi‖(2εT+ηi‖DBi‖)= ((1-qT)2-1)ST(k)S(k)-[2εT(1-qT)+2ηi(1-qT)‖DBi‖]‖S(k)‖+ (εT)2+ηi‖DBi‖(2εT+ηi‖DBi‖)。 (36) 由式(32)~(37)式可知,当‖S(k)‖>ζ时 ΔV(k)≤0 (37) 这意味着准滑动模态于有限时间可达,并且系统状态轨迹将一直维持在准滑动模态区域内。 注5: 由定理2可知,在准滑动模态区域外有‖S(k+1)‖<‖S(k)‖,即系统状态轨迹将于有限时间内到达准滑动模态,并且准滑动模态的带宽 满足下式 考虑含有两个模态的切换系统(1), 系统参数如下: 子系统1: 子系统2: ε11=32.849 7, ε12=32.246 2 ε21=37.779 4, ε22=37.260 9 因此,滑模面设计为 由定理1可知,参数μ和Tσ分别设计为 因此,可以得到参数μ=1.163 5 平均驻留时间设计为Tσ=1.5。 选择参数ε=0.5、q=2,系统采样时间选为T=0.1 s。由式(30)和(31)得滑模控制律为 (a) 切换信号σ(k) (b) 状态轨迹x(k) (c) 滑模面S(k) (d) 控制信号u(k) 本文采用输入矩阵加权方法设计了一个公共滑模面,考虑了一类不确定离散切换系统的滑模控制,采用平均驻留时间方法分析了系统的指数稳定性。结果表明,在采样时间、参数不确定性以及外界扰动的不良影响下,设计的滑模控制律能保证系统状态轨迹于有限时间内被趋使到准滑动模态上并一直维持在该区域运动。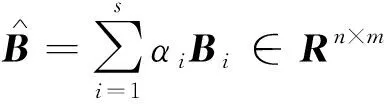
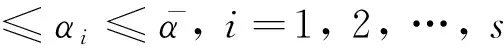
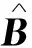
2 滑模面和准滑动模态
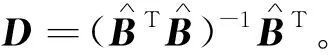



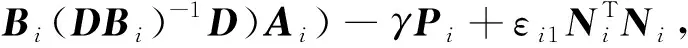

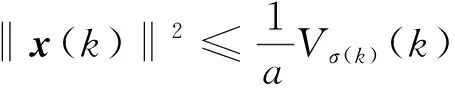
3 滑模控制器设计
(DBi)-1εTsgn(S(k))-Gi(k)



4 数值仿真






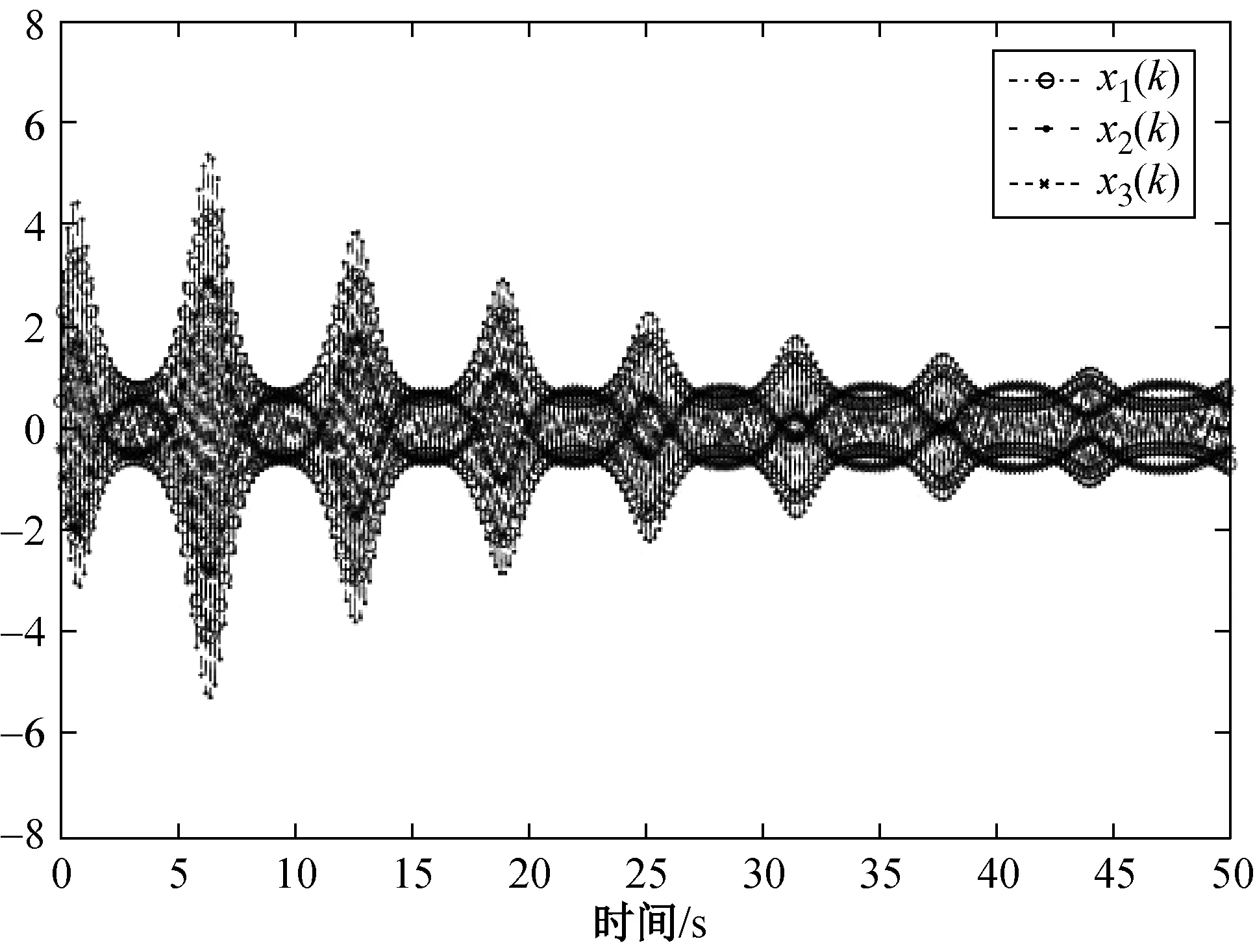

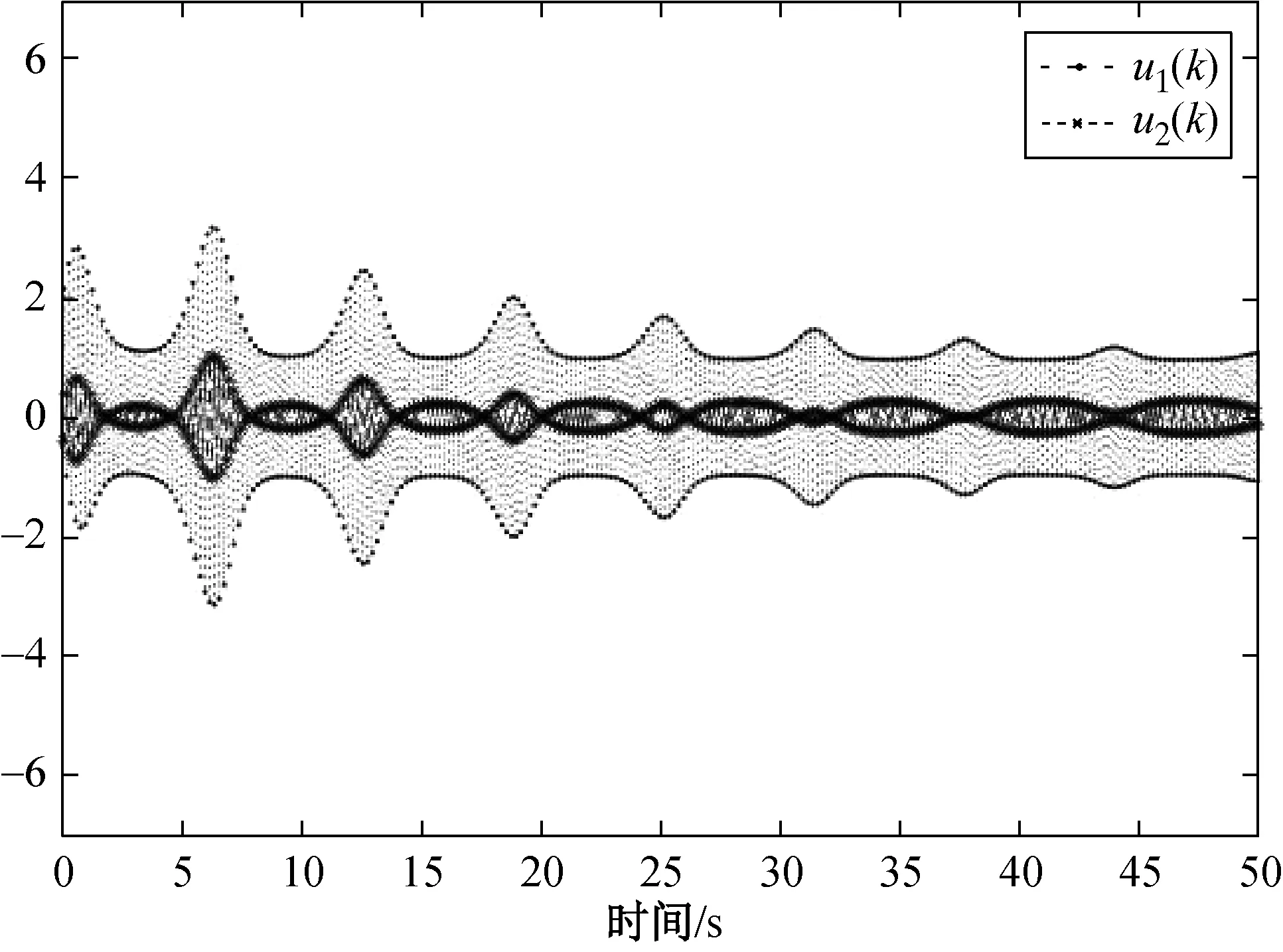
5 结 语