奇异随机微分方程的依分布几乎自守解
2018-07-19蒋慧杰
常 晶, 赵 昕, 蒋慧杰
(吉林农业大学 信息技术学院, 长春 130118)
随机微分方程的几乎自守解在力学、物理、统计学和生物数学等领域应用广泛. 几乎自守函数是几乎周期函数的推广, 由于几乎自守现象在符号动力系统中表现出某种复杂性和混沌现象, 因此得到广泛关注. 付苗苗等[1]首先引入了几乎自守过程, 此后关于随机微分方程几乎自守解的研究得到深入发展[2-3]. 但关于依分布几乎自守解的研究目前文献报道较少, 文献[4-6]得到了随机微分方程的依分布几乎自守解; 陈锋等[7]得到了依状态切换的随机微分方程的几乎自守解. 奇异线性系统在网络理论等领域应用广泛[8-9]. Diagana等[10]研究了奇异随机微分方程均方意义下的几乎周期解. 本文利用文献[10-11]中块对角化的技巧, 考虑奇异随机微分方程依分布意义下的几乎自守解.
1 预备知识
设(H,‖·‖) 是可分的Hilbert空间,W(t)为定义在概率空间(Ω,F,P,(Ft)t≥0)上的布朗运动, 其中Ft=σ(W(u)-W(v)|u,v≤t),L2(Ω,H )为所有H值随机变量x组成的空间, 且
设(U,‖·‖U)为可分的Hilbert空间,L(U,H )是从U到H的所有有界线性算子空间.
定义1[7]对于随机过程x(t):→L2(P,H ), 如果对所有的s∈, 有

定义2[7]对于L2-连续随机过程x(t):→L2(P,H ), 如果对于序列⊂, 存在一个子列sn⊂和一个随机过程y(t):→L2(P,H ), 使得
对所有的t∈都成立, 则称x(t)是二阶矩意义下几乎自守的.
定义3[7]对于一个连续随机过程x, 如果t→μt∶=μ(x(t)):→Pr(C(,X))是几乎自守的, 则称x为依分布几乎自守的, 其中μ(x(t))∶=P∘[x(t)]-1为P下分布的.
则称x(t)是依分布几乎自守的.
2 主要结果
考虑奇异随机微分方程
Adx(t)+Bx(t)dt=f(t)dt+g(t)dW(t),t∈
(1)
依分布的几乎自守解, 其中:A:D(A)⊂H→H,B:D(B)⊂H→H是闭的线性算子, 且D(B)⊆D(A);f:→L2(Ω,H ),g:→L(U,H )为几乎自守随机过程;W(t)是U-值布朗运动.B(H )表示所有有界线性算子H的集合,D(S),ρ(S),N(S)和R(S)分别表示线性算子S的定义域、豫解式、值域和像集, 且R(λ,S)∶=(λI-S)-1, 其中:λ∈ρ(S);I: H→H为H的单位算子. 假设f,g为几乎自守的随机过程, 且线性算子B有一个有界逆. 因为B有连续逆, 且D(B)⊂D(A), 定义T=AB-1: H→H为连续线性算子, 则R(λ,T)=(λI-T)-1:ρ(T)→B(H ). 利用文献[8-9], 令Bx=y,x∈D(B)⊂D(A), 则方程(1)可化为
Tdy(t)+y(t)dt=f(t)dt+g(t)dW(t),t∈.
(2)
且H =R(T)⊕N(T)=X1+X2. 显然, 由R(λ,T)定义知,T为限制在X1=R(T)上的有界逆算子, 则T可写为
其中M为限制在X1上的有界线性算子.T也可视为X1上的C0半群. 利用T的对角块形式及f,g两个随机过程分别在X1和X2上的投影分解:
方程(2)可分解为
M-1dy1(t)+y1(t)dt=f1dt+g1(t)dW(t),y2(t)=f2(t)+g2(t).
(3)
则y=(y1,y2)有如下形式:
(4)
其中t,τ∈且t≥τ. 则式(3),(4)可等价地写成如下等式:
(5)
其中t,τ∈且t≥τ.
假设原点的C0-半群T(t)=(e-Mt)t≥0是指数稳定的, 即存在常数K≥1和ω>0, 使得
‖T(t)‖X1≤Ke-ωt,t≥0.
定理1如果f,g为几乎自守的, 则方程(1)存在唯一依分布的几乎自守解.
证明: 首先y为方程(1)的有界温和解, 下面证明y是方程(3)的唯一几乎自守解. 要证y2是几乎自守过程, 只需证y1满足方程(4)也是几乎自守过程.y1可化为


即
对所有的t∈均成立. 利用Cauchy-Schwarz不等式, 可得
其中F为几乎自守函数. 类似地, 因为g1也是几乎自守的, 则对于>0, 有
因为



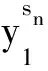
下面证明解的唯一性. 令
为方程(1)在分布意义下的两个几乎周期解, 再令w1=u1-v1, 可得w1=e-M(t-s)w1(s). 当t≥s时,w1有界, 则对所有的t≥s, 有
令(τn)n∈, 当n→∞时,τn→-∞, 对于任意固定的t∈, 存在子序列(τnk)k∈, 使得对于所有的k∈, 有τnk
