孙莹 张伟

(非线性振动及机械结构强度北京市重点实验室, 北京工业大学机械工程与应用电子技术学院, 北京 100124)

引言

环形桁架天线具有大口径、重量轻、灵敏度高、拓扑结构简单等特点,是目前大型卫星天线的较为理想的结构形式.由于结构尺寸大以及材料的柔韧性等自身结构特点,环形桁架天线在空中展开后易出现变形,外加复杂的太空环境如：太阳辐射、热激励和微重力等,天线展开锁定后在运行中易导致大幅的非线性振动.其振动形式主要有以下四种类型：(1)环形桁架与展开臂的整体弯曲振动;(2)环形桁架绕展开臂的面内扭转振动;(3)环形桁架绕展开臂的横摇振动;(4)环形桁架面内的呼吸振动.此外,还存在上述四种振动模态之间的非线性耦合振动.所以越来越多的国内外学者对于环形桁架天线的非线性动力学行为展开了详细的研究. Makarov等人[1]研究了环形柔性可展天线在稳定状态下的动力学行为.张等人[2]建立了环形桁架天线的运动方程,并分析了在1∶2内共振下的非线性动力学行为.孙和张等人[3]利用能量相位法研究了环形桁架天线的全局分岔和多脉冲混沌运动.胡等人[4,5]建立了大型可展天线展开锁定后在空中运行的动力学模型并分析了其动力学特性,而且还研究了一种由两个刚性臂所支撑的大型空间可展天线的非线性动力学行为.范震等人[6]分析了大型空间环行天线结构振动的前四阶模态,并且研究了材料参数和边界条件对振动模态和固有频率的影响.

由于大幅振动严重影响卫星天线的结构性能以及稳定性,所以研究卫星天线运行中的稳定性变得尤为重要.而通常用高维非线性系统描述大型可展开天线的动力学行为.因此,可以利用高维非线性系统的局部分岔理论研究大型可展天线在临界点附近可能发生的复杂动力学行为.近些年,国内外学者在高维非线性系统的局部分岔问题研究方面取得了一些成果.Yu等人[7]研究了双摆系统的稳定性并给出了分岔解的稳定性条件.陈等人[8-10]利用理论和数值方法分析了不同非线性系统平衡点的稳定性和分岔解. Wei等人[11-13]针对不同的三维自治系统应用Routh-Hurwitz判据研究了系统的稳定性、分岔行为以及混沌吸引子等.徐等人[14]利用规范型理论和中心流型定理分析了具有负阻尼的延迟振子的Hopf 分岔及稳定性.

本文利用高维非线性理论以及数值方法研究了1∶1内共振情况下环形桁架天线的稳定性以及分岔特性. 在文献[2] 所建立的运动方程的基础上,利用多尺度法得到直角坐标系下的平均方程. 根据中心流形理论、非线性变换以及Routh-Hurwitz判据等得到了环形桁架天线的临界条件. 分析了环形桁架天线平衡点附近的稳定性, 并通过数值计算验证了理论分析的准确性.

1 运动方程

在文献[2]中环形桁架天线被简化成等效圆柱壳结构模型,其动力学模型如图1所示.为了研究环形桁架天线在实际情况下能够产生何种内共振情形,利用有限元方法对实际可展天线结构进行仿真,通过模态分析得到天线结构的振动频率.根据有限元的模态析,给出了第四阶和第五阶振动模态,如图2和图3所示.同时,得到了环形桁架天线前五阶振动模态频率,如图4所示.从图2,3和4中可以看出第四阶模态和第五阶模态的振动频率比接近1∶1.因此,在第四阶模态和第五阶模态之间可能出现1∶1内共振关系.所以,本文研究了环形桁架天线在1∶1内共振下的稳定性以及非线性动力学行为.

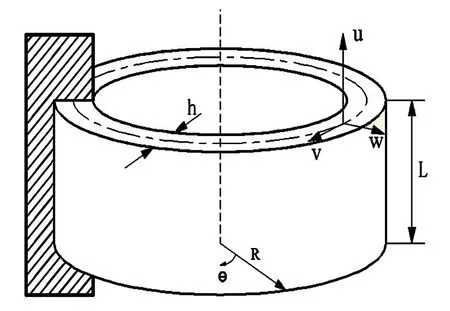
图1 等效圆柱壳模型Fig.1 Model of equivalent circular cylindrical shell

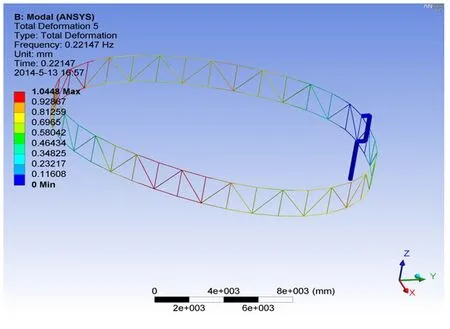
图2 环形桁架天线第四阶振动模态Fig.2 The fourth order mode in vibration of the circular truss antenna

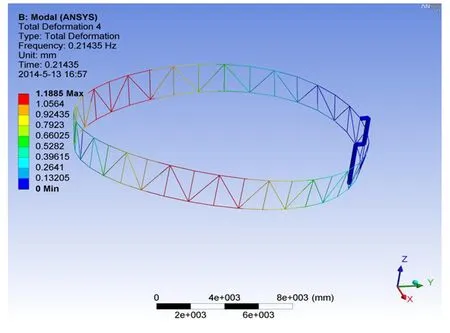
图3 环形桁架天线第五阶振动模态Fig.3 The fifth order mode in vibration of the circular truss antenna

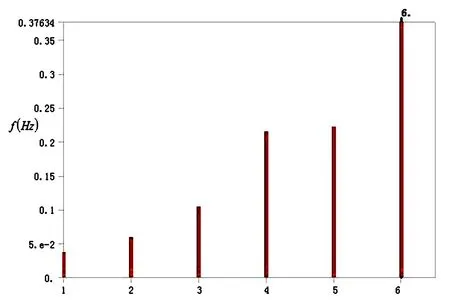
图4 环形桁架天线振动频率Fig.4 The vibration frequency of the circular truss antenna

根据一阶剪切变形理论,von Karman几何关系以及Hamilton原理得到了等效圆柱壳的非线性偏微分方程,利用Galerkin方法对偏微分方程进行离散,我们主要考虑系统的横向非线性振动,得到了两自由度等效圆柱壳非线性呼吸振动常微分方程如下：

γ12w2+γ13w13+γ14w12w2+γ15w1w22+

γ16w23=γ17+γ18fTcos(Ωt)

(1a)

γ22w1+γ23w23+γ24w22w1+γ25w2w12+

γ26w13=γ27+γ28fTcos(Ωt)

(1b)

其中,w1(t)和w2(t)分别是第四阶和第五阶振动的模态函数,fT为环形桁架天线的外激励,μ1和μ2为结构阻尼系数.

利用多尺度法分析等效圆柱壳的非线性呼吸振动方程,为了便于分析,引入如下参数变换：

γ11→εγ11,γ12→εγ12,γ13→εγ13,

γ14→εγ14,γ15→εγ15,γ16→εγ16,

γ17→εγ17,γ21→εγ21,γ22→εγ22,

γ23→εγ23,γ24→εγ24,γ25→εγ25,

γ26→εγ26,γ27→εγ27,μ1→εμ1,

μ2→εμ2

(2)

考虑1∶1内共振情形,关系如下：

(3)

经过计算,得到四维直角坐标系下的平均方程：

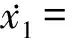
(4a)

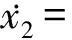
(4b)

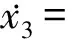
(4c)

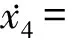
(4d)

2 稳定性和分岔分析

根据坐标平移原理,微分方程的非零平衡点都可以平移到零解平衡点处,因此,我们只需考虑零解平衡点附近的稳定性.

由方程(4)可知,(x1,x2,x3,x4)=(0,0,0,0)为方程的平衡点,对应的Jacobian矩阵为：

(5)

Jacobian矩阵(5)对应的特征多项式如下：

f(λ)=a0λ4+a1λ3+a2λ2+a3λ+a4

(6)

其中,

a0=1

(7a)

a1=μ1+μ2

(7b)

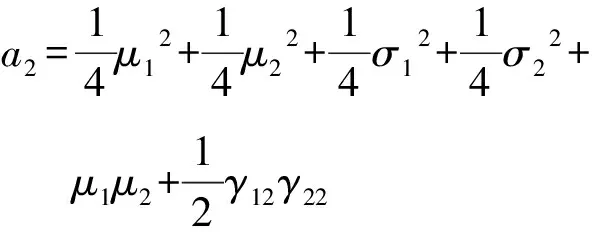
(7c)

(7d)

(7e)

根据Routh-Hurwitz判据可知,如果平衡点(x1,x2,x3,x4)=(0,0,0,0)是稳定的,系统必须同时满足如下条件：

a1>0,a1a2-a3>0,a4>0

a3(a1a2-a3)-a12a4>0

(8)

条件(8)表明Jacobian矩阵(5)的所有特征根实部均为负数.而当条件(8)中有任何一个条件不满足时,平衡点即为不稳定解,系统将会出现分岔现象.因此,接下来我们将要对系统(4)进行局部稳定性和分岔分析.

如果Jacobian矩阵(5)只有一个零特征根,对应的特征多项式(6)只有一个零解,则需要多项式(6)的系数a1,a2,a3,a4满足a1·a2·a3≠0,a4=0.即如下条件：

(9)

根据方程(9),继续推导得出：

μ1μ2-σ1σ2+γ12γ22=0,

(μ1σ2+μ2σ1)2=0

(10)

将方程(10)代入(7d)中,得到a3=0.如果条件a3=0和a4=0同时满足,则会得到Jacobian矩阵(5)将有一对零特征根,这个结果与矩阵(5)有一个零特征根的结论相违背.因此,Jacobian矩阵(5)不可能存在只有一个零解的情况. 下面我们分析特征多项式(6)在平衡点处有双零和两个负特征值以及双零和一对纯虚特征值情形下的稳定性.

2.1 双零和两个负特征根

在这一节中,我们主要研究特征多项式(6)在平衡点处有双零和两个负数特征根的情况.为了便于分析,选取方程(4)中的参数如下：μ1=μ2=2,γ13=γ14=γ15=γ16=8,γ12=2,γ22=-4 ,γ23=γ24=γ25=γ26=8,σ2=-2,σ1=2 ,γ18=γ28=0,其中γ12,γ13,γ14,γ15,γ16,γ23,γ24,γ25,γ26为系统的几何结构参数,因此这些参数值只能取正或者零.γ22=-4为一组可以进行代数运算的几何参数,正直或者负值均可取,取负值时系统在平衡点处有两个负特征根,为稳定状态.σ1和σ2为系统的调谐参数,既可取负值又可取正值.参数则方程(6)对应的特征多项式和特征根为：

f(λ)=λ4+4λ3+4λ2=0,

λ1,2=0,λ3,4=-2

(11)

选取μ1和μ2作为摄动参数,引入摄动变换μ1=2+ε1和μ2=2+ε2. 给出如下的稳定性变换：

(12)

将变换(12)代入方程(4),系统被改写成为如下形式：

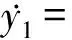
(13a)

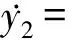
(13b)

(13c)

(13d)

其中,非线性项Ngi(i=1,2,3,4)的表达式见附录A.

由中心流形降维方法可以知道系统(12)的局部动力学行为由变量y1和y2决定,而非主变量y3和y4的分岔解利用变量y1和y2来表示,可得到y3和y4的表达式如下：

(14a)

(14b)

将方程 (14)代入方程 (13),在方程(13)的前两个方程中忽略y3和y4两个变量,这种研究方法不影响(y1,y2)的分岔解和稳定性条件.因此,要研究系统(13)的平衡点处的分岔和稳定性问题,只需分析降维后的二维系统,该系统如下：

(15a)

(15b)

(16a)

(16b)

根据不等式(16) ,定义稳定性临界曲线如下：

(17a)

L2:ε1-ε2=0

(17b)

L3: [(ε1-ε2)2-8ε1](ε1-ε2-8)-64=0

(17c)

根据方程(17),可得平衡点的稳定性区域分布图,如图5所示.临界曲线L1,L2和L3将平面(ε1,ε2)分为稳定区域和不稳定区域,其中多项Ⅰ为稳定区域,Ⅱ为不稳定区域.

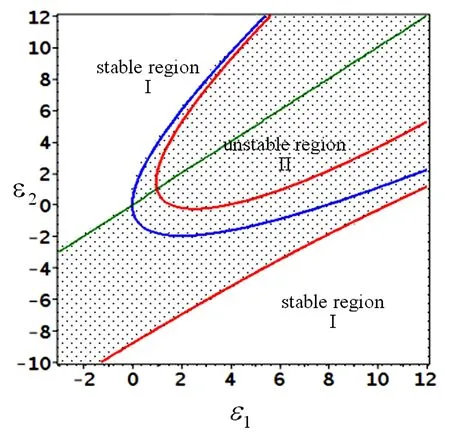
图5 双零和两个负数特征根的稳定区域以及不稳定区域Fig.5 Stable region and the unstable region for the case of a double zero and two negative eigenvalues

为了验证理论分析结果的有效性,我们对平均方程(4)进行数值分析.在稳定区域Ⅰ中选取参数值(z1,z2,z3,z4)=(0.002,0.001,0.003,0.001)和(ε1,ε2)=(-0.5,0.1),我们得到图6.从图6中可以观察到相空间中的轨线是周期轨线,因此轨线是稳定的周期轨道.同理,在不稳定区域II中选取参数值(z1,z2,z3,z4)=(0.003,0.001,-0.03,0.001)和(ε1,ε2)=(0.5,-0.2),得到图7.根据图7可以观察到,轨线是从中心向外盘旋运动远离初始点,所以该轨线是不稳定的.

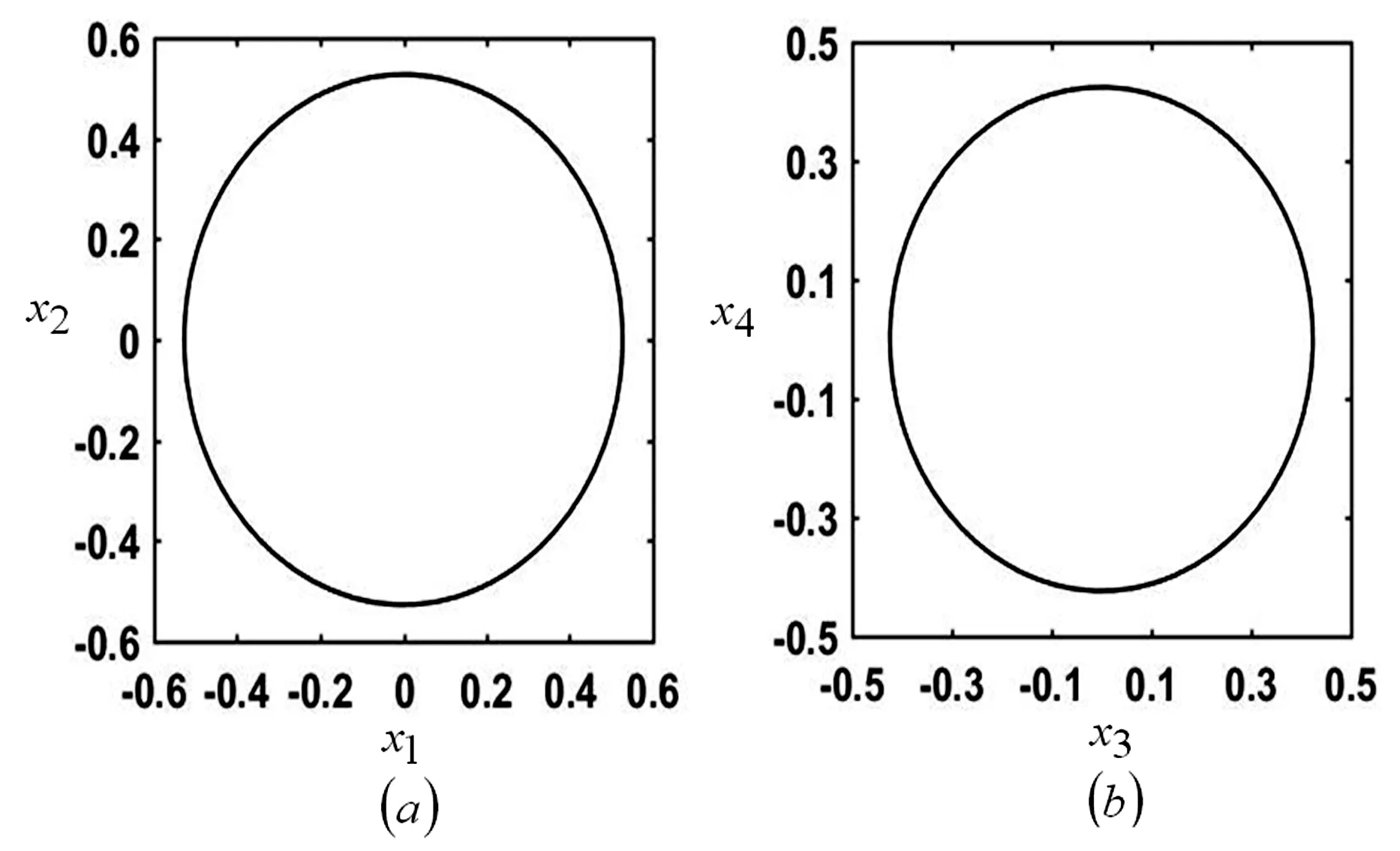
图6 稳定区域内的轨迹Fig.6 Trajectory of the stable region

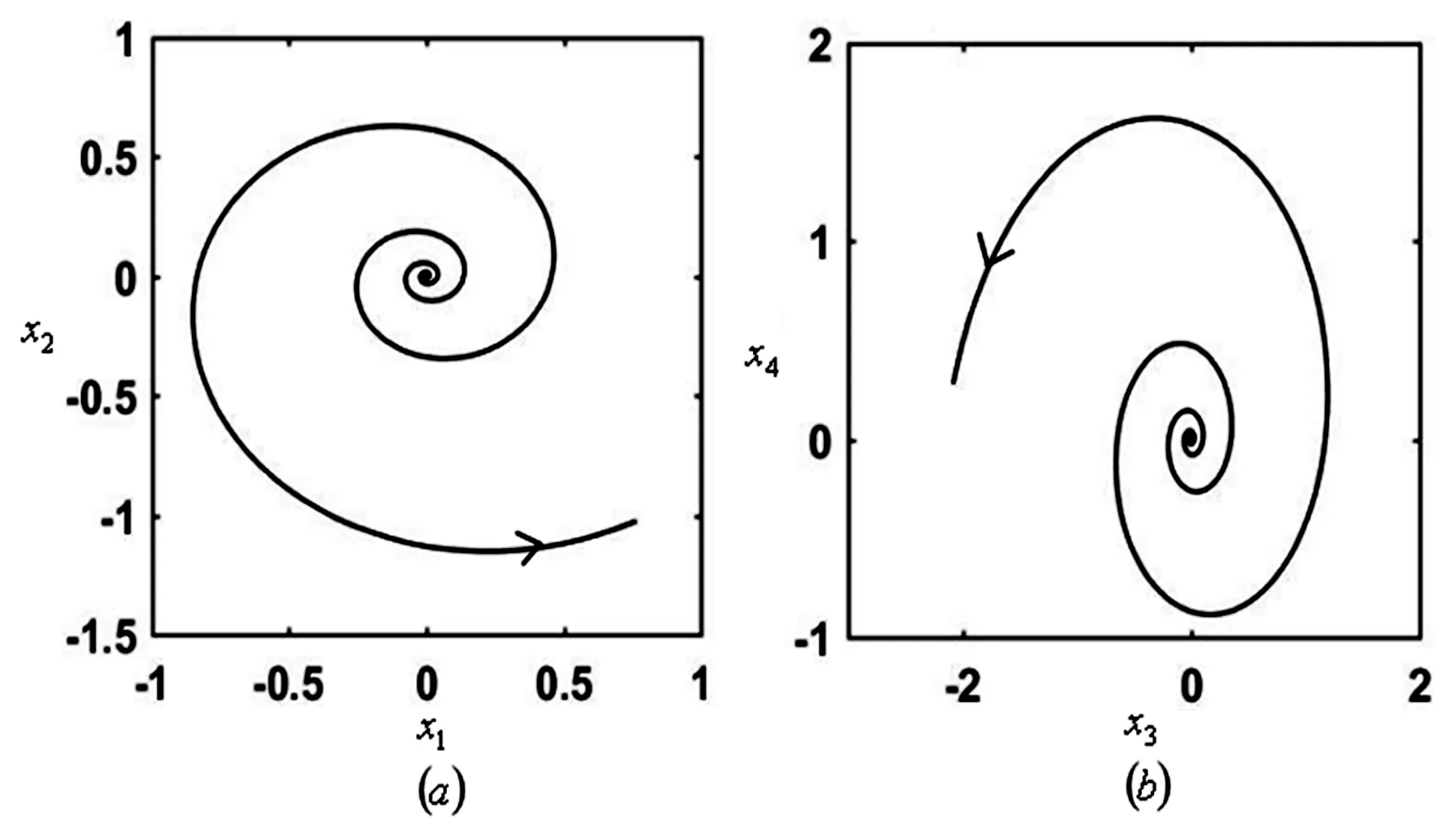
图7 不稳定区域内的轨迹Fig.7 Trajectory of the unstable region

2.2 双零和一对纯虚复数特征根

在本小节,我们研究特征多项式(6)在平衡点处有双零和一对纯虚复数特征根的情况.为了便于分析,我们选取方程(4)中的参数如下：μ1=μ2=0,σ1=σ2=γ12=γ22=1.则方程(6)对应的特征多项式和特征根为：

f(λ)=λ4+λ2,λ1,2=0,λ3,4=±i

(18)

选取μ1和μ2作为摄动参数,引入摄动变换μ1=ε1和μ2=ε2.将摄动变换代入Jacobian矩阵(5),则Jacobian矩阵(5)对应的特征多项式可以写成如下形式：

f(λ)=λ4+c1λ3+c2λ2+c3λ+c4

(19)

其中,

c1=ε1+ε2

(20a)

(20b)

(20c)

(20d)

根据Routh-Hurwitz判据可知,如果平衡点是稳定的,则需要满足如下条件：

ε1+ε2>0

(21a)

(21b)

(21c)

从不等式(21)中可以观察到：当不等式(21c)成立时,不等式(21b)也一定成立.则根据不等式(21),我们可以定义稳定区域的临界曲线如下：

L4:ε1+ε2=0

(22a)

(22b)

根据方程(22)可以得到平衡点的稳定性区域分布图,如图8所示. 临界曲线L4和L5将平面(ε1,ε2)分成稳定区域和不稳定区域,其中Ⅰ代表稳定区域, Ⅱ代表不稳定区域.

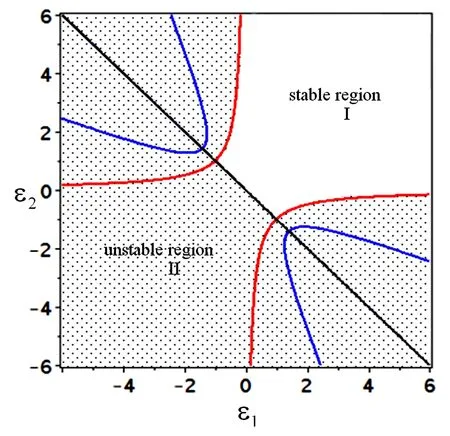
图8 双零和一对纯虚复数特征根的稳定区域以及不稳定区域Fig.8 Stable region and the unstable region for the case of a double zero and a pair of purely imaginary eigenvalues

同上,在不同的区域内选取不同的参数值验证理论分析.首先我们在稳定性区域I中选取参数值(z1,z2,z3,z4)=(0.002,0.001,0.003,0.001)和(ε1,ε2)=(-0.5,0.1),我们得到图9. 从图9中可以明显观察到,相空间轨线从初始点逐渐盘旋趋于平衡点达到稳定状态.在不稳定区域II中选取参数值(z1,z2,z3,z4)=(0.003,0.001,-0.03,0.001)和(ε1,ε2)=(0.5,-0.2),得到图10.如图10所示,轨线从初始点起呈螺旋状向外运动,偏离初始点,轨线是不稳定的.

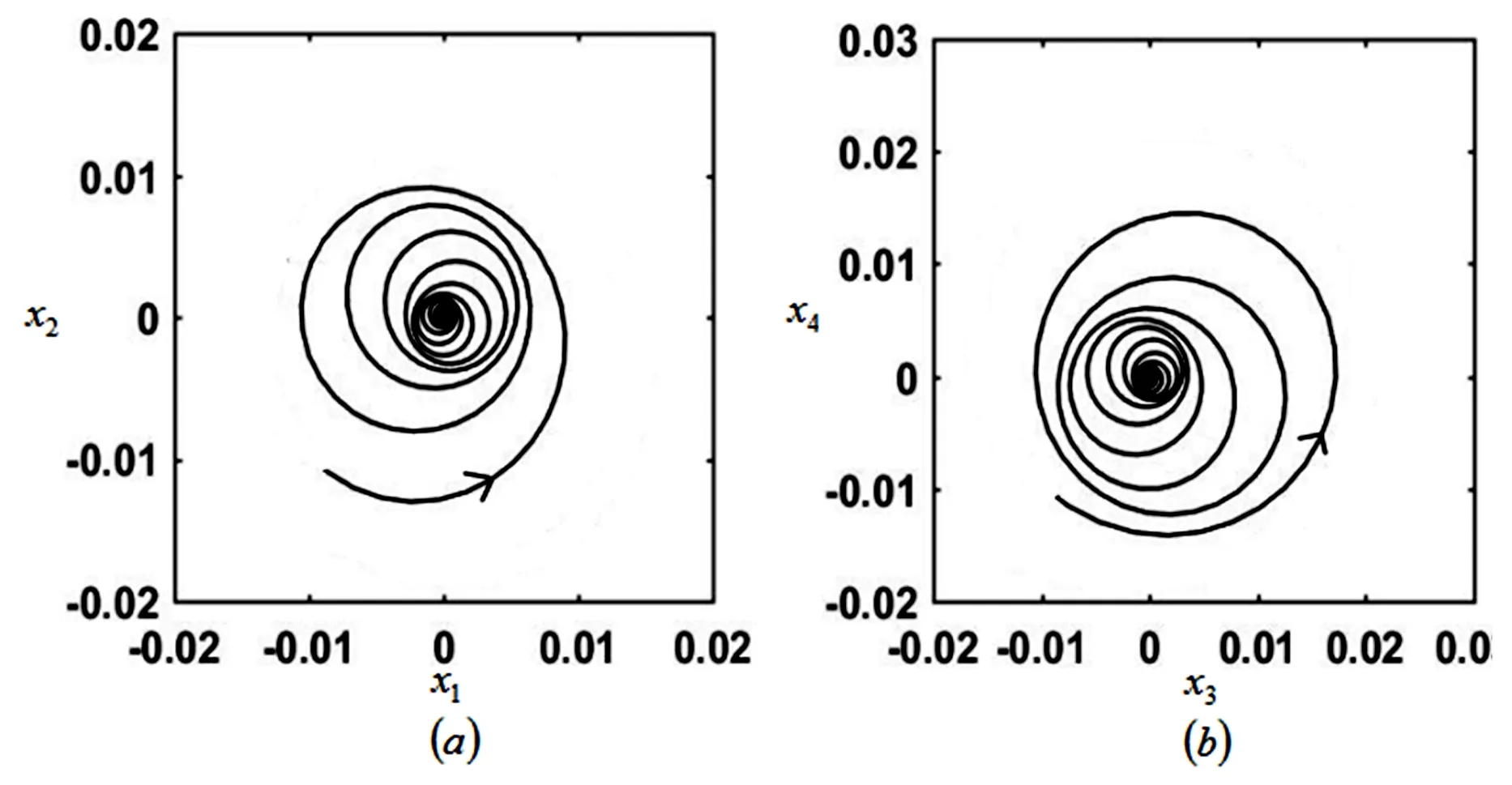
图9 稳定区域内的轨迹Fig.9 Trajectory of the stable region

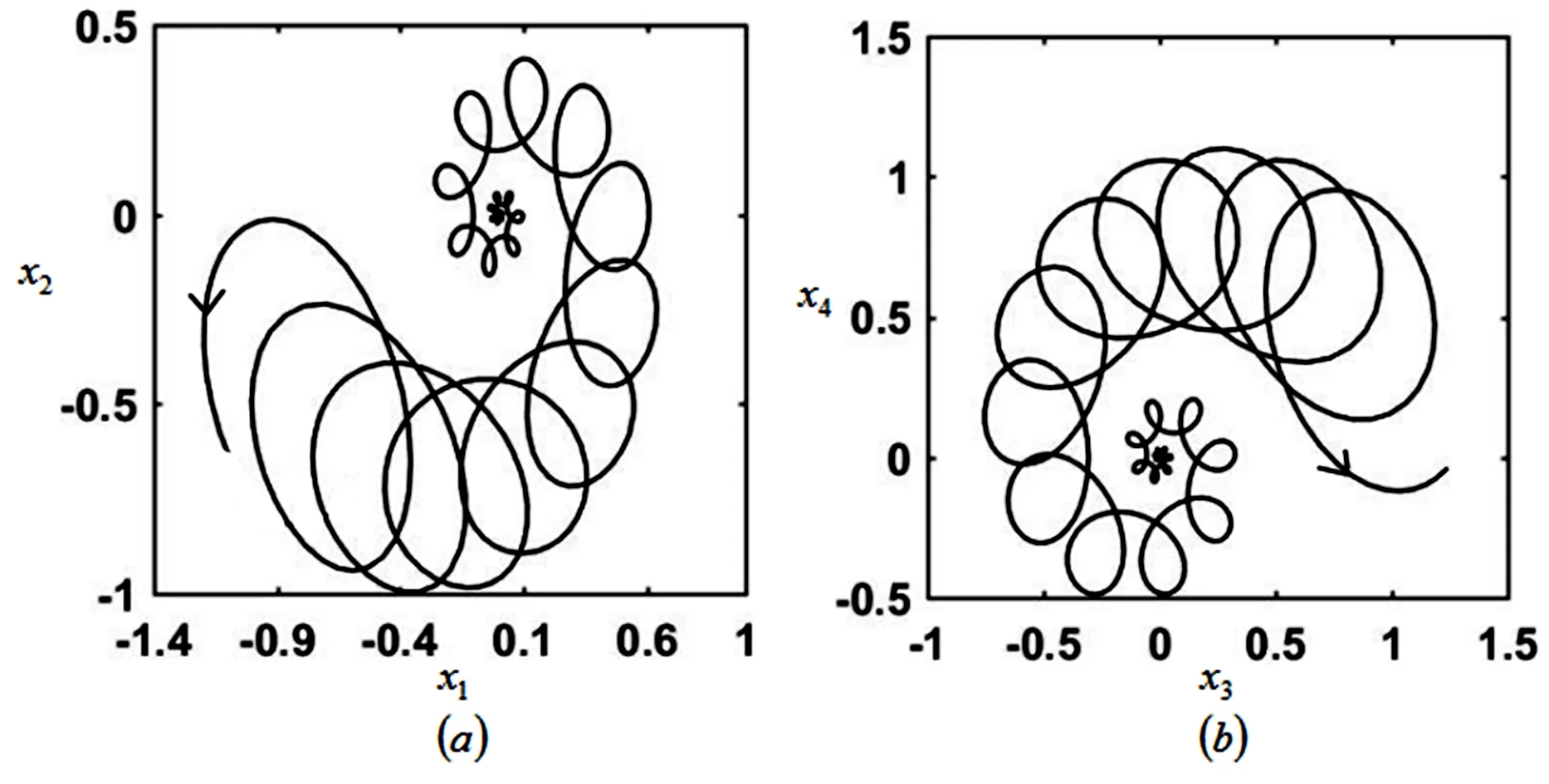
图10 不稳定区域内的轨迹Fig.10 Trajectory of the unstable region

3 结论

本文研究了1∶1内共振情形下环形桁架天线的局部分岔问题,即平衡点附近的1*.稳定性和非线性动力学行为.通过理论分析,我们得到了两种不同形式下平衡点的稳定区域以及不稳定区域,分别是平衡点为双零和两个负数特征根情形以及平衡点为双零和一对纯虚复数特征根情形. 根据四维平均方程进行数值分析,选取不同的参数研究环形桁架天线系统的稳定性.在不同的区域内选取参数值,得到相应的相空间轨线图,轨线图进一步验证了数值计算和理论分析的一致性.通过所得到的数值计算和理论分析研究结果,可以优化环形桁架天线系统的结构设计以及调控系统参数,从而预防和避免环形桁架天线在运行中产生大幅振动.

1Makarov A L, Khoroshilov V S, Zakrzhevskii A E. Spacecraft dynamics due to elastic ring antenna deployment.ActaAstronautica, 2011,69(7):691～702

2Zhang W, Chen J, Sun Y. Nonlinear breathing vibrations and chaos of a circular truss antenna with 1∶2 internal resonance.InternationalJournalofBifurcationandChaos, 2016,26(5):1650077

3Sun Y, Zhang W, Yao M H. Multi-pulse chaotic dynamics of circular mesh antenna with 1∶2 internal resonance.InternationalJournalofAppliedMechanics, 2017,9(4):1750060

4胡海岩,田强,张伟等. 大型网架式可展开空间结构的非线性动力学与控制. 力学进展, 2013,43(4):390～414 (Hu H Y, Tian Q, Zhang W, et al. Nonlinear dynamics and control of large deployable space structures composed of trusses and meshes.AdvancesinMechanics, 2013,43(4):390～414 (in Chinese))

5Gao X M, Jin D P, Hu H Y. Internal resonances and their bifurcations of a rigid-flexible space antenna.InternationalJournalofNon-LinearMechanics, 2017,94:160～173

6范震,郭翔鹰,张伟.大型空间环型天线结构动力学分析. 动力学与控制学报, 2016,14(1):41～47 (Fan Z, Guo X Y, Zhang W. Dynamics analysis of large deployable mesh antenna structure.JournalofDynamicsandControl, 2016,14(1):41～47 (in Chinese))

7Yu P, Bi Q. Analysis of non-linear dynamics and bifurcations of a double pebdulum.JournalofSoundandVibration, 1998,217(4):691～736

8Zhang D M, Chen F Q. Stability and bifurcation of a cantilever functionally graded material plate subjected to transversal excitation.Meccanica, 2015,50(6):1403～1418

9Yu W Q, Chen F Q, Li N, et al. Stability and bifurcation dynamics for a nonlinear controlled system subjected to parametric excitation.ArchiveAppliedMechanics, 2016,87(3):479～487

10 Zhang L, Chen F C. Stability and bifurcation for limit cycle oscillations of an airfoil with external store.NonlinearDynamics, 2016,10(1):1403～1418

11 Wei Z C, Pham V T, Kapitaniak T, et al. Bifurcation analysis and circuit realization for multiple-delayed Wang-Chen system with hidden chaotic attractors.NonlinearDynamics, 2016,85(3):1635～1650

12 Wei Z C, Yang Q G. Dynamical analysis of a new autonomous 3-D chaotic system only with stable equilibria.NonlinearAnalysis:RealWorldApplications, 2011,12(1):106～118

13 Wei Z C, Zhang W. Hidden hyperchaotic attractors in a modified Lorenz-Stenflo system with only one stable equilibrium.InternationalJournalofBifurcationandChaos, 2014,24(10):1450127

14 Xu X, Hu H Y, Wang H L. Stability, bifurcation and chaos of a delayed oscillator with negative damping and delayed feedback control.NonlinearDynamics, 2007,49(49):117～129