论固有振型的节点规律
2018-07-09胡海岩
胡海岩
(北京理工大学宇航学院 飞行器动力学与控制教育部重点实验室, 北京 100081)
引言
线性时不变系统(本文简称系统)的固有振型节点概念源自两端固定的细弦作固有振动时会呈现波节现象.波节是弦上的非完全约束点集(即除去端点以外的点),其在某阶固有振动中保持静止.对于细梁、薄板和厚板等弹性体,通常将其固有振动时保持静止的非完全约束点集称为节点、节线和节面.对于由惯性元件、弹性元件构成的离散系统,通常将系统作固有振动时保持静止的非完全约束点集称为节点,尽管其可能具有一维或二维特征.节点概念在工程实践中具有重要地位,是判断固有振动阶次、布置实验激振点和测振点的依据,也是振动设计和振动控制的依据之一.
人们很早就发现,固有振型阶次与节点数目间存在一定关系.例如,1892年Routh在其专著中指出,细弦横向振动的第r阶固有振型有r-1个节点[1];Sturm和Liouville则研究了直杆纵向振动的固有振型节点分布规律[2].自上世纪30年代起,Гантмахер和Крейн对固有振型节点规律进行了深入研究,并在40年代初出版的专著中分别讨论了多种离散和连续系统,指出其第r阶固有振型有r-1个节点.虽然该专著的中译本到2008年才问世[3],但我国学者早就在译著、教材和手册中广泛引用该结论[4-6],甚至称结论适用于一般线性系统.
事实上,Гантмахер和Крейн主要采用柔度法研究离散系统或采用影响系数法研究段状连续系统,通过振荡矩阵或振荡核表示,分析特征向量分量或特征函数的正负号变化规律,并称其为振动的振荡性质[3].他们研究的离散系统具有振荡性质的柔度矩阵,可包含Sturm系统,其质量矩阵、刚度矩阵分别为对角矩阵和标准Jacobi矩阵.而段状连续系统则是指弦、杆、梁、轴等一维弹性结构,其Green函数是振荡核函数.虽然许多线性系统满足上述条件,但仅仅是线性系统中的一类.例如,周荣仁列举了一个6自由度离散系统的反例,其固有振型不满足上述节点规律[7].又如,对于内周固支的环形薄板或循环对称叶盘,其最低阶固有振型有一条节线,而某阶高阶振型却没有节线[8].然而,人们在引用Гантмахер和Крейн的结论时,常常忽略这些前提,导致结论被泛化.庆幸的是,近年来王大钧等对Гантмахер和Крейн的研究结果进行了系统梳理和推广,明确了弦、杆、轴、梁及其离散系统的固有振动具有振荡性质[9].
本文试图对离散系统固有振型的节点概念作进一步探讨,纠正流行的不妥结论.文中对两自由度系统的固有振型节点规律进行全面分析,获得若干新结论.基于这一分析,对一类多自由度组合系统的固有振型进行讨论,说明其节点的可设计性.
1 对现有理论的反思
1.1 离散系统固有振型节点规律概述
Гантмахер和Крейн的研究从Sturm系统开始,其典型代表是链式集中质量—弹簧系统、带集中惯性元件的弦、杆和轴等.这类系统的动力学模型是二阶偏微分方程,其离散模型的质量矩阵是对角矩阵,刚度矩阵是标准Jacobi矩阵,即主对角元素为正、次主对角元素为负的三对角阵.他们用初等方法证明:对于Sturm系统,无论其是否有刚体运动,系统固有频率无重频,其第r阶固有振型有r-1个节点[3].事实上,Sturm系统最多只有1个刚体运动模态,对应于第1阶固有频率为零且固有振型无节点;此后第r阶固有振型必有r-1个节点.
对于带集中质量的梁,其动力学模型是四阶偏微分方程,离散模型的刚度矩阵不再是标准Jacobi矩阵;更一般的系统亦如此.在系统无刚体运动模态前提下,Гантмахер和Крейн采用影响系数法建立用系统柔度矩阵表示的特征值问题,证明若柔度矩阵是振荡矩阵,则系统固有频率无重频,其第r阶固有振型必有r-1个节点[3].他们的重要贡献是给出了任意方阵是振荡矩阵的判据,即同时满足非奇异、完全非负、次对角主元素为正这三个条件[3].
对于具有刚体运动模态的梁,王其申等通过引入共轭梁概念研究了固有振型阶次与节点数之间的关系[10].对于铰支—自由这类仅含1个刚体运动模态的梁,具有与Sturm系统完全一致的结论.值得指出的是,自由—自由梁具有2个刚体运动模态,即梁的前2阶固有频率均为零,该重频固有振型是2个线性无关的刚体运动.若定义第1阶固有振型为梁沿弯曲方向的平动,无节点;第2阶固有振型是绕质心的转动,有1个节点;将弹性振动模态从r=3起升序排列,则自由—自由梁的第r阶固有振型有r-1个节点.
1.2 广义坐标问题
在振动分析及计算中,人们用系统质量矩阵、刚度或柔度矩阵所确定的特征向量来描述其固有振型,并认为特征向量的相邻坐标分量变号意味着固有振型有节点.特别当某坐标分量为零时,则认为该坐标原点就是节点.值得指出,系统质量矩阵、刚度或柔度矩阵依赖于广义坐标,而广义坐标的选取具有灵活性,会对固有振型的表示产生影响.
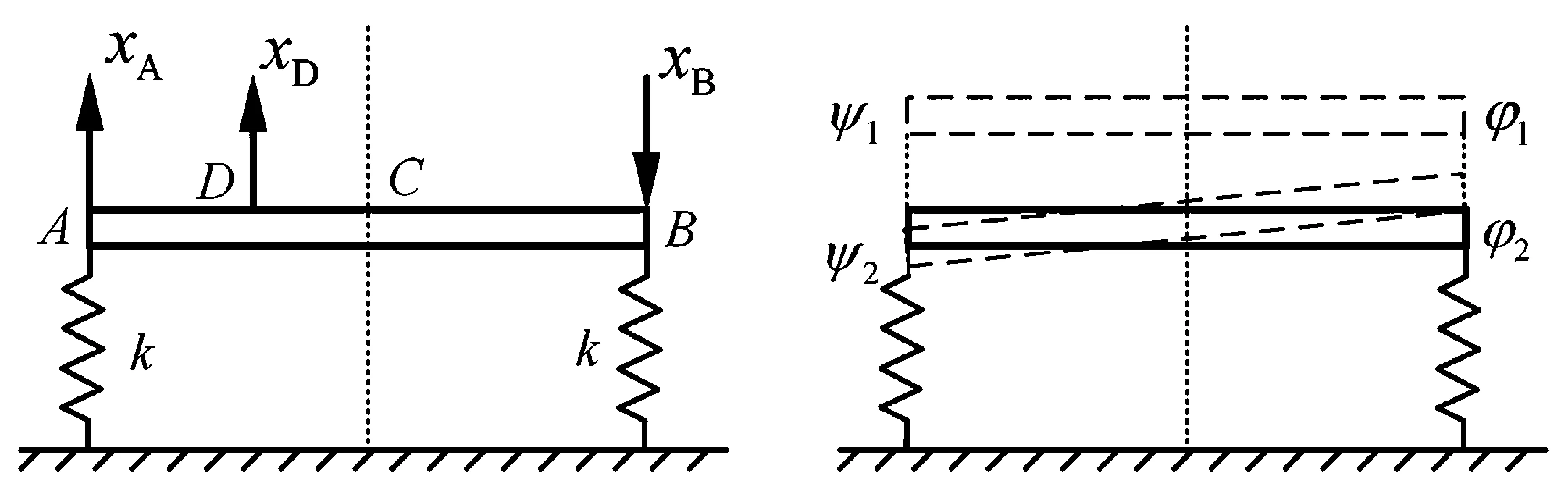
图1 两自由度对称系统及其固有振型Fig.1 A symmetric system of two degrees of freedom and its natural mode-shapes
考察图1所示系统,其中刚性杆AB的质量m均匀分布,两个弹簧的刚度均为k且质量可忽略不计.对于该两自由度系统,其广义坐标可选用刚性杆上任意两个点的铅垂位移.现讨论两种情况:
(1)选用刚性杆两端的xA和xB作为广义坐标,根据系统对称性可得到系统固有模态:
(1)
由于xA和xB的方向不一致,导致φ1的两个分量符号相反,但它并无节点;而φ2的两个分量符号一致,但却有节点,且位于刚性杆的质心.
(2)选用xA和位于AC中点xD作为广义坐标,则系统固有模态为:
(2)
虽然ψ2的两个分量符号一致,但仍以刚性杆质心为节点.事实上,φr和ψr描述了完全相同的几何量,r=1,2.
注解1:固有振型是一个可以比例伸缩的几何量,本质上不依赖系统广义坐标;但为了研究方便,必须借助某种广义坐标系描述的特征向量;离开了所选定的广义坐标系,特征向量就失去了几何意义,而仅仅是一个数组.
注解2:上述两组广义坐标说明,在振动分析中不能仅仅根据特征向量相邻分量是否变号来断言固有振型是否具有节点,还必须回到所选的广义坐标中考察系统固有振型的几何形态,判断是否有节点.
注解3:广义坐标的选取灵活多变,给研究固有振型节点规律带来困难.因此,Гантмахер和Крейн主要研究一维振动系统,选取指向一致的广义坐标[3],此时特征向量的相邻分量变号则表明固有振型存在节点.但上述第2组广义坐标说明,固有振型可能在一维系统端部广义坐标原点的外侧出现节点.因此,特征向量的相邻分量变号只是判断固有振型节点的充分条件,而并非必要条件.
1.3 振荡矩阵问题
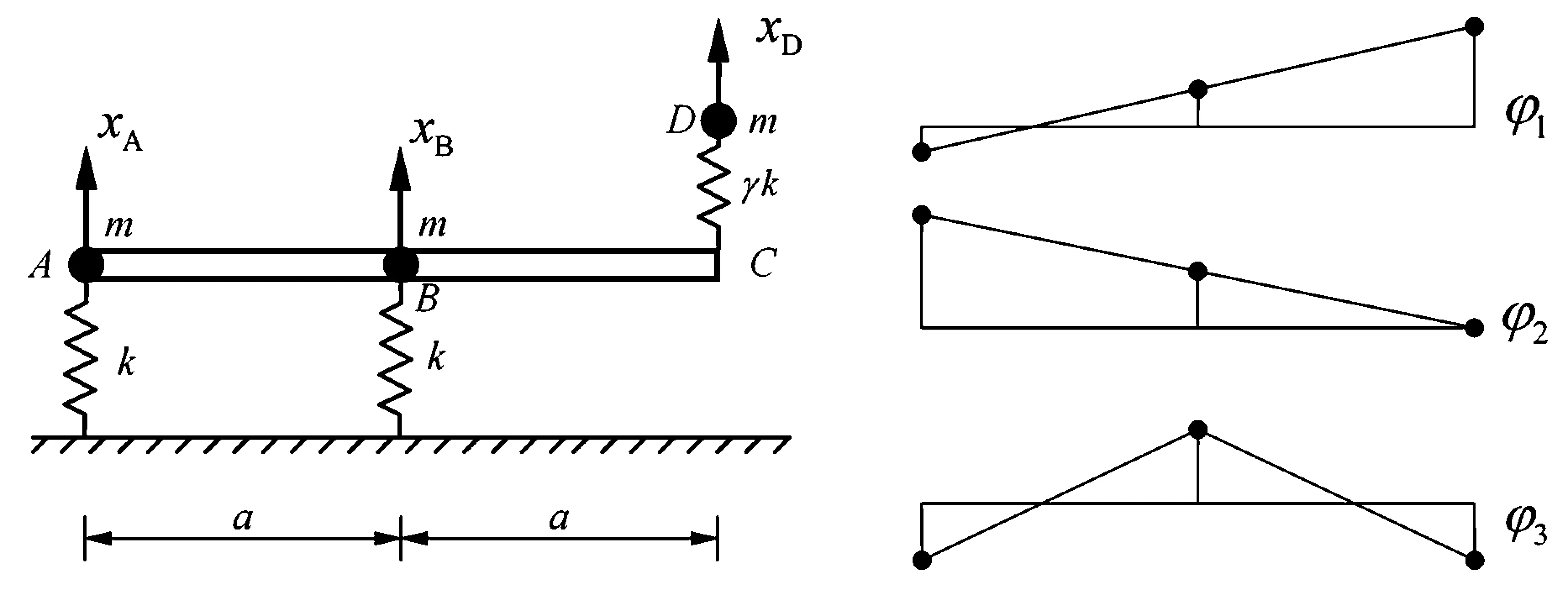
图2 三自由度系统及γ=100时的固有振型Fig.2 A system of three degrees of freedom and its natural mode-shapes when γ=100
考察图2所示3自由度系统,其中3个集中质量均为m,刚性杆AC和弹簧的质量均忽略不计;左侧和中间弹簧的刚度均为k,右侧弹簧的刚度为γk,γ>0为无量纲系数.在图2所定义的广义坐标系中,系统动能和势能分别为:
(3)
此时系统质量矩阵、刚度矩阵和柔度矩阵分别为:
(4)
对于γ=1和γ=100,求解矩阵束(M,K)的广义特征值问题,得到系统固有模态:
γ=1:
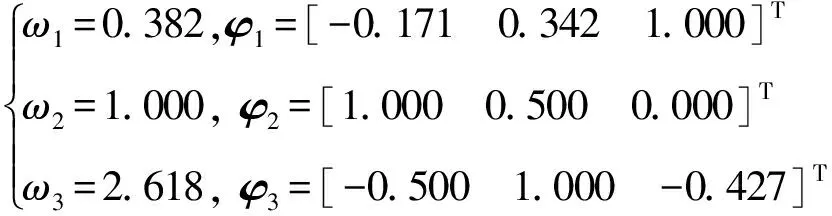
(5)
γ=100:
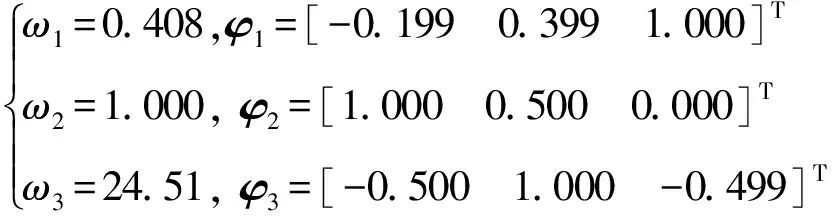
(6)
对比式(5)和式(6)可见,右支承刚度变化对系统固有模态影响不大,1.4节将讨论该刚度趋于无穷的情况.该系统前两阶固有振型均有1个节点,第3阶固有振型有2个节点.
注解1:虽然该系统的质量矩阵是对角矩阵,但刚度矩阵K不是标准Jacobi矩阵[3],无法依据Sturm系统理论判断固有振型的节点数.
注解2:虽然该系统形如链式系统,但柔度矩阵F的次对角元素包含零,不满足振荡矩阵条件[3],故无法用Гантмахер和Крейн的研究结果来判断固有振型的节点数.
1.4 惯性耦合问题
仍考察图2所示系统,取γ→+∞,即右端集中质量固定在刚性杆右端,此时系统只有两个自由度.在图2定义的广义坐标xA和xB描述下,系统动能和势能分别为:
(7)
该系统具有惯性耦合,质量矩阵和刚度矩阵分别为:
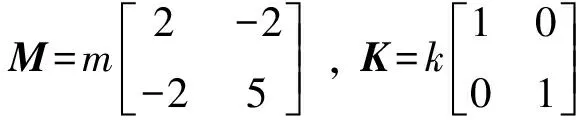
(8)
求解广义特征值问题,得到系统的固有模态为:
(9)
在选定的广义坐标下,这两阶固有振型均有节点.将式(9)与式(6)对比可见,此时的固有振型与图2中前两阶固有振型相差无几.
注解1:在Гантмахер和Крейн的研究中,对具有集中质量的离散系统采用影响系数法,故系统质量矩阵没有惯性耦合项[3].虽然本例中的系统形如链式系统,但其具有惯性耦合项,故采用Гантмахер和Крейн的研究结果已无法处理这类系统.
注解2:系统惯性耦合项导致固有振型的节点规律更为复杂,甚至出现两自由度系统的每个固有振型均有节点.
2 两自由度系统固有振型的节点规律
2.1 一般性分析
考察两自由度振动系统,选取方向一致的两个广义坐标,建立系统的质量矩阵M∈R2×2和刚度矩阵K∈R2×2,记系统固有频率矩阵和关于模态质量归一的固有振型矩阵分别为;
(10)
φ1rφ2r≤0,r=1,2
(11)
现研究上式成立的条件.
根据固有振型矩阵关于质量矩阵、刚度矩阵的加权正交性,即ΦTMΦ=I和ΦTKΦ=Λ,可导出:
M=Φ-TΦ-1,K=Φ-TΛΦ-1
(12)
故它们的次对角线元素为:
(13)
由上式可得到系统物理参数与模态参数之间的关系:
(14)
现对式(14)分两种情况进行讨论.
c. 对于情况b的特例m12=0,即系统在这组广义坐标下惯性解耦,有如下更为简洁的结果:若k12<0,则φ2有节点;若k12=0,则φ1和φ2均有节点;若k12>0,则φ1有节点.由于此时系统质量矩阵是对角阵,而根据伴随矩阵概念可推知当k12<0时,系统柔度矩阵是振荡矩阵,故属于Гантмахер和Крейн的研究覆盖范畴.除此之外,该系统还有产生节点的其它情况,这是该理论无法预计的.
图3是依据上述结论在(m12,k12)平面上确定的4个区域及其边界.该图直观地给出了固有振型节点数与系统的惯性耦合项、弹性耦合项以及固有频率之间的关系.
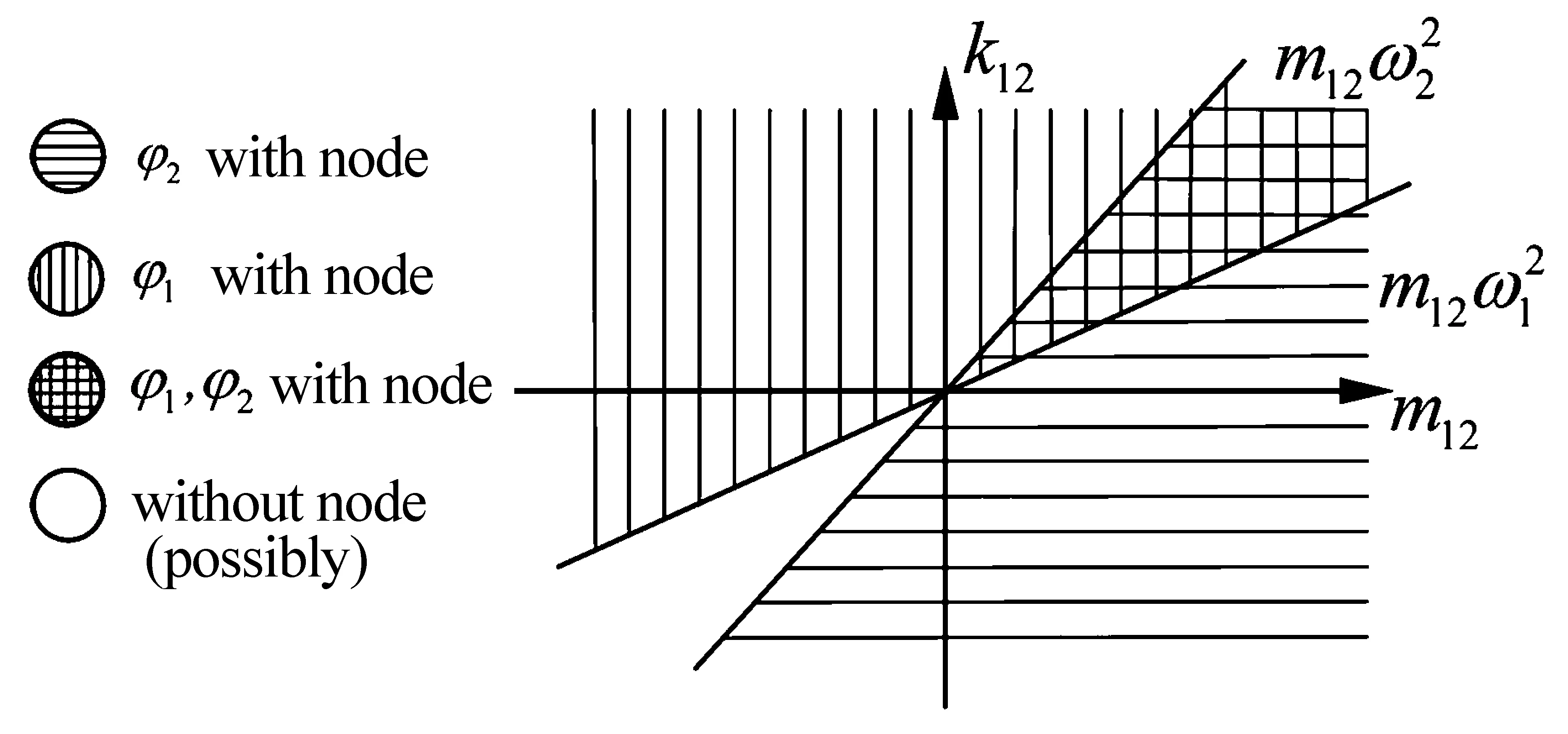
图3 任意两自由度系统的固有振型分类Fig.3 Classification of the natural mode-shapes of an arbitrary system of two degrees of freedom
(15)
该系统的阻抗矩阵满足:
A(ω0)=0
(16)
因此,任意两个线性无关的非零向量均是系统固有振型,且它们的线性组合亦如此.由此可得到两自由度系统重频固有振型的节点性质:
a. 两个固有振型可以均无节点,或均有节点,或仅其中之一有节点.
b. 可以选择系统上任意一点,并找到某个固有振型以该点作为其节点.
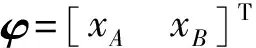
最后需要指出,Гантмахер和Крейн的研究仅适用于不含重固有频率的系统,自然无法覆盖此处的复杂情况.
2.2 案例分析
考察图4所示的两自由度系统,其中刚性杆AB的质量m均匀分布,长度为ηL,η≥1是无量纲系数;两个弹簧的距离为L,刚度分别为k1和k2,质量忽略不计.现取杆端部向上位移xA和xB为广义坐标,研究不同杆长及弹簧刚度情况下的固有振型.
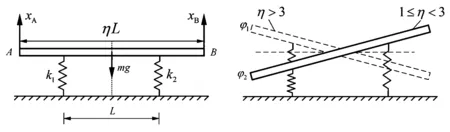
图4 两自由度系统及等刚度支承时的固有振型Fig.4 A system of two degrees of freedom and its natural mode-shapes when two mountings are identical
在图4定义的广义坐标xA和xB描述下,系统的动能和势能分别为:
(17)
由此可得到系统的质量矩阵和刚度矩阵:
(18)
以下针对两个弹簧刚度是否相同进行讨论.
(1)若两个弹簧刚度相等,记为k1=k2=k,则式(18)简化为:
(19)
(20)
显然,反对称固有振型以刚性杆中心为节点,但其对应的固有频率阶次取决于参数η.
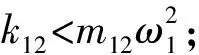
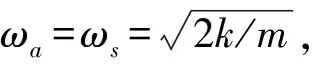
(2)若两个弹簧刚度不等,不妨约定0 (21) 系统的两个固有模态为: (22) 注解1:虽然此处讨论一个简化的两自由度系统,但它对于采用空气弹簧作为支承的飞机地面振动试验具有参考价值.相对于空气弹簧的刚度而言,飞机刚度高许多,试验中测量到的前两阶固有振动,就是空气弹簧支承飞机在铅垂面内的刚体运动.若空气弹簧的间距足够大,则第1阶固有振型无节点,第2阶固有振型有1个节点;第3阶固有振型近似于飞机在自由状态下最低频率的弯曲固有振型,有2个节点;更高阶固有振型的节点数可依次类推.显然,若空气弹簧的间距过小,则前两阶固有振型出现节点的顺序会颠倒. 注解2:本节的一般性分析和案例分析说明,两自由度系统的固有振型节点规律远比人们通常的认识要复杂.特别当系统具有惯性耦合或重固有频率时,已超出了Гантмахер和Крейн的研究结果范畴. 当系统自由度数超过2之后,很难再按2.1节的思路去分析固有振型的节点问题.本节分析一类多自由组合系统的固有振型节点问题,试图说明其固有振型的节点可设计性. 图5 n+1自由度组合系统Fig.5 A composite system of n+1 degrees of freedom 考察图5所示组合系统S≡S1∪S2的固有振动问题.其中,S1是n自由度系统,其阻抗矩阵为Bn(ω)≡[bij(ω)]∈Rn×n;S2是具有重固有频率ω0的两自由度系统,其质量矩阵为M≡[mij]∈R2×2,根据式(16)知对应的阻抗矩阵可表示为: (23) 在组合系统S中,约定将S1的第1个自由度x1与S2的第2个自由度y2刚性对接,故组合系统的阻抗矩阵为: Zn+1(ω)= ∈R(n+1)×(n+1) (24) 根据行列式的Laplace展开公式,可由式(23)得到组合系统的固有频率方程: a11(ω)detBn(ω)+detA(ω)·detBn-1(ω)=0 (25) 将式(23)代入上式,得到: (26) 根据式(26),组合系统的其余n个固有频率满足方程: (27) =0 (28) (29) 由此可得到: (30) 注解1:由于两自由度系统S2具有重频,故存在使其第2个广义坐标为零的固有振型,且S2与S1耦联后可保持该固有振型不变.即组合系统以S2的固有频率振动时,S1的各自由度均保持静止,而仅有S2的第1个自由度发生振动. 注解2:这种固有振型与S1的具体形式无关,所以可选择适当的S2,使该阶固有振动发生在所需频段上,而且是S2的局部振动.这种振动模式有别于将S2设计为动力减振器,使S1在S2的联结点处发生反共振.事实上,当组合系统反共振时,S1的其它自由度依然振动. 注解3:如果将2.2节中的案例作为S2并且取η2=3,则S2具有重固有频率,可验证上述结论. (1)系统固有振型是一个几何量,但其研究和计算需要借助系统广义坐标.对于作一维振动的链式系统,可选取指向一致的广义坐标系,进而根据Гантмахер和Крейн的理论来判断特征向量的相邻分量是否变号,再结合广义坐标来确定固有振型是否有节点.对于链式系统,有必要检查节点是否出现在端点广义坐标原点的外侧. (2)具有广泛影响的Гантмахер和Крейн理论的应用范围并非所有线性系统,甚至并非所有链式系统;尤其当系统存在惯性耦合时,该理论可能会失效.如果系统具有重固有频率,则该理论必然失效. (3)对两自由度系统的固有振型研究表明,其两个固有振型可能均无节点,或均有节点,甚至可能其中任意一个有节点. (4)将具有重固有频率的两自由系统与任意的多自由度系统相耦合,可使组合系统在原两自由度系统上产生局部共振,而原多自由度系统静止,从而人为设计组合系统的固有振型阶次与节点数目的关系. 1Routh E J. Dynamics of a system of rigid bodies. London: Macmillan, 1892 2Rayleigh L.The theory of sound, 2ndedition. New York: Dover, 1945 3甘特马赫,克列因. 振荡矩阵、振荡核和力学系统的微振动. 王其申 译. 合肥: 中国科学技术大学出版社, 2008 (Гантмахер Ф Р, Крейн М Г. Осцилляционные матрицы и ядра и малые колебания механических систем. Москва: Государственное Издательство Технико-Теоретической Литературы, 1950 (in Chinese)) 4巴巴科夫. 振动理论(上册). 薛中擎译. 北京:人民教育出版社, 1962 (Babakov I М. Theory of vibrations. Beijing: Press of People′s Education, 1962 (in Chinese)) 5贺兴书. 机械振动学. 上海:上海交通大学出版社, 1985 (He X S. Mechanical vibration. Shanghai: Press of Shanghai Jiaotong University, 1985 (in Chinese)) 6机械工程手册、电机工程手册编辑委员会. 机械工程手册,第4卷第21篇. 北京:机械工业出版社, 1982 (Editorial board of manuals of mechanical engineering and motor engineering. Manual of mechanical engineering, Volume 4, Chapter 21. Beijing: Machinery Industry Press, 1982 (in Chinese)) 7周荣仁. 关于节点定理. 力学与实践, 1986,8(2):23~26 (Zhou R R. On the node theorem.MechanicsandPractice, 1986,8(2):23~26 (in Chinese)) 8胡海岩,程德林. 循环对称结构固有模态特征的探讨. 应用力学学报, 1988,5(3):1~8 (Hu H Y, Cheng D L. Modal characteristics of a cyclo-symmetric structure.ChineseJournalofAppliedMechanics, 1988,5(3):1~8 (in Chinese)) 9王大钧,王其申,何北昌. 结构力学中的定性理论. 北京:北京大学出版社, 2014 (Wang D J, Wang Q S, He B C. Qualitative theory of structure mechanics. Beijing: Peking University Press, 2014 (in Chinese)) 10 王其申,王大钧. 存在刚体模态的杆、梁离散系统某些振荡性质的补充证明. 振动工程学报, 35(2):262~269 (Wang Q S, Wang D J. Supplementary proof of some oscillation property for discrete systems of rod and beam having rigid modes.ChineseQuarterlyofMechanics, 35(2):262~269 (in Chinese)) 11 胡海昌. 多自由度结构固有振动理论. 科学出版社, 1987 (Hu H C. Natural vibration theory of structures of multiple degrees of freedom. Beijing: Science Press, 1987 (in Chinese))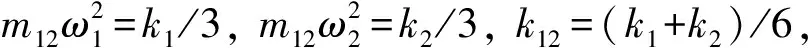
3 固有振型节点的可设计性
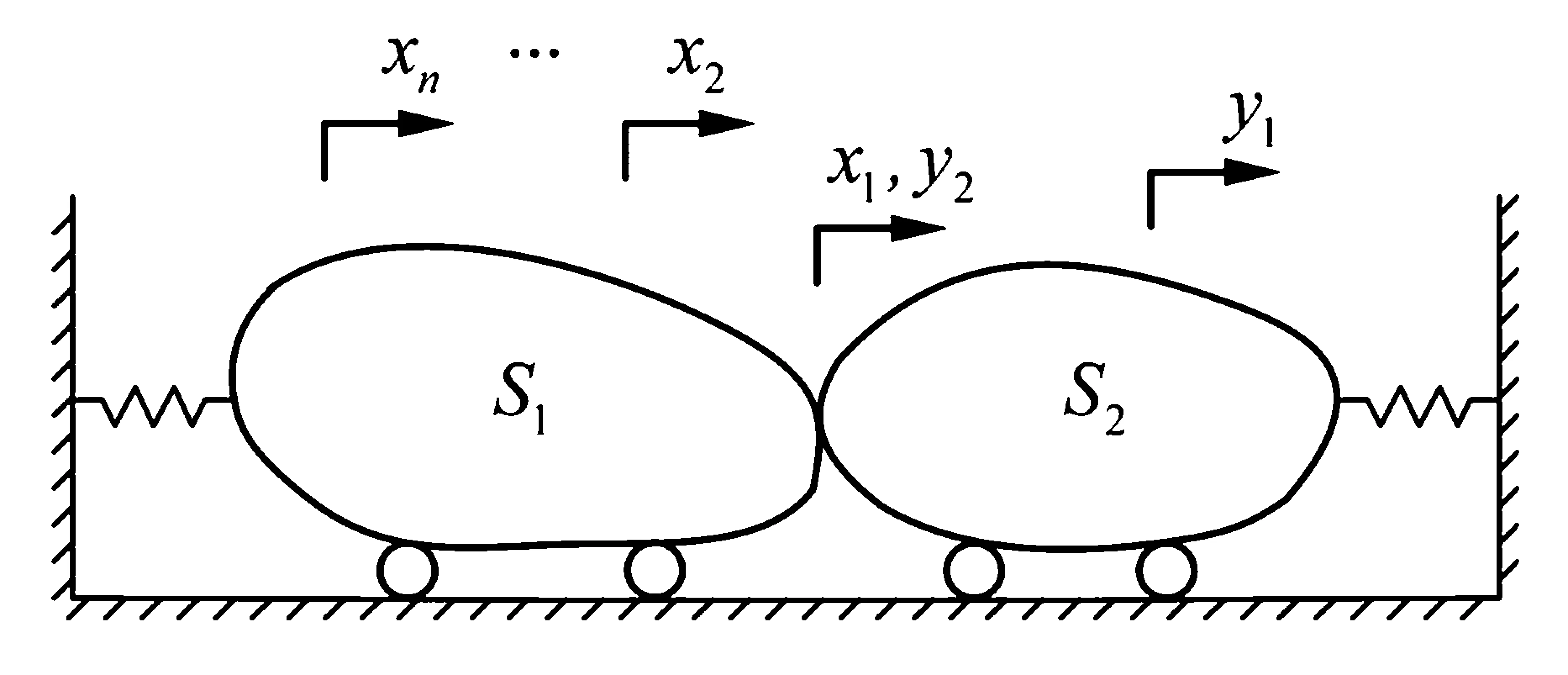

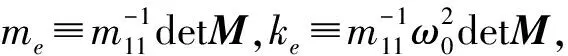
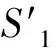

4 结论
