王 琪

(贵阳学院数学与信息科学学院， 贵州 贵阳 550005)

0 引言

2004年， Alencar等[1]研究球面空间Sn+1中常高阶平均曲率的紧致无边超曲面， 建立起一类积分公式， 并通过这些公式， 利用高斯映像来刻画超曲面的全脐性质得到了定理1. 文献[2]研究欧氏空间Rn+1中以低维球面为边界, 具有常数高阶平均曲率的紧致超曲面. 其建立了相应的积分公式， 同时利用高斯映照的一种条件， 讨论超曲面的性质， 得到了定理2. 本研究讨论欧氏空间Rn+1紧致无边超曲面, 通过一个已知的积分公式， 并采用一种新的“分割”技巧， 利用高斯映照来刻画超曲面的性质， 得到了一个新的定理， 即以下定理3.

1 预备知识

设n维黎曼流形M等距浸入到一个(n+1)维黎曼流形中， 并设λi(1≤i≤n)是M的主曲率函数， 则M第r阶高阶平均曲率Hr有以下定义[1-4]:

同时定义H0≡1.

当M可定向时，M具有整体的单位法向量场N. 记Sn是n维标准单位球面， 则M的Gauss映照定义为

φ:M→Sn，φ(p)=N(p) (∀p∈M)

需要使用一个积分公式， 即下列引理1.

引理1[4]设M是Rn+1中紧致无边定向超曲面. 用x表示M在Rn+1中的位置向量，N表示M的光滑单位法向量场. 则以下积分公式成立

其中： 〈, 〉表示Rn+1的欧氏内积， dx表示黎曼流形M的n维黎曼体积元.

2 主要结果

定理1[1]设M是单位球面Sn+1空间中紧致无边超曲面. 假设M的某一个高阶平均曲率Hr(1≤r≤n-1)是正常数， 同时下列不等式处处成立

Hr-1≥0，H1Hr-1≥Hr>0

如果M的高斯映照像落在一个闭的半球面内， 则M是全脐的.

定理2[2]设M是Rn+1中定向紧致带边界超曲面， 且假设M的某个高阶平均曲率Hr(2≤r≤n)是常数， 同时M⊂π的边界为圆球面Sn-1. 如果M的高斯映照像落在一个超平面π的一侧， 则M一定是n维圆盘或球面盖.

定理3设M是Rn+1中紧致无边定向凸超曲, 且M的某一个高阶平均曲率Hr(1≤r≤n-1)是常数. 如果M的高斯映照是到标准单位球面Sn的拓扑同胚， 则M是全脐的.

证明 因为M是凸的， 所以M整个落在其每一点之切超平面的一侧， 则可以适当选择M的单位法向量场的指向， 那么在M的每一点处， 其主曲率函数λi(1≤i≤n)均为非负.

因为M是紧致无边的， 根据文献[4]的论证，M必有严格椭圆点， 即： 在该点处必有Hr>0.

而本研究假设Hr是常数， 所以有

Hr>0 (∀x∈M)

根据文献[1-2]， 产生代数不等式

结合以上两式有

Hi>0， ∀x∈M(i=1, 2, …,r)

根据另外一个熟知的代数不等式[1-8]， 可得

∀x∈M(i=1, 2, …,r)

(1)

由以上分析立即有

H1≥H2/H1≥…≥Hr/Hr-1≥Hr+1/Hr(∀x∈M)

(2)

现在， 应用引理1的积分公式， 有

(3)

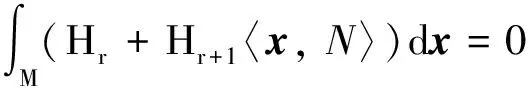
(4)

因为Hr为常数， 由式子(3)可得

(5)

再由式子(4)～(5)可知

(6)

注意到式子(2)则有

H1Hr-Hr+1≥0 (∀x∈M)

(7)

为完成证明， 本研究将采用“分割法”： 即分部分来证明M的脐性.

首先， 因为M是凸的和闭的， 所以M必定包围一个(n+1)维的凸区域D. 则M恰是某个凸区域D的边界， 即M=∂D.

任意取定D的一个内点O∈D， 并且以点O作为Rn+1的原点.

任意取定Rn+1的一个通过原点的n维超平面n， 即Σn是Rn+1的一个线性子空间. 同时记Sn是n维标准单位球面.

记

Σn-1=Sn∩Σn=Sn-1

则Σn-1=Sn-1即是Sn的一个(n-1)维赤道， 而Σn就是相应的n维赤道面.

因为Σn经过Rn+1的原点， 所以可以假定

Σn={x=(x1, …,xn,xn+1)∈Rn+1:xn+1=0}

今写M的单位法向量场N为

N=(τ1, …,τn,τn+1)

并记

注意到本研究的假设： 高斯映射φ:M→Sn是拓扑同胚， 若记

则M的这三个部分互不相交， 而且

M=M+∪M-∪M0

现在， 可以将式子(6)重新写作

(8)

其中

以下分别估计上面三项：A、B和C.

首先， 因为假设高斯映射φ:M→Sn是拓扑同胚， 而拓扑映射保持维数不变， 所以M0=φ-1(Sn-1)是Rn+1中一个(n-1)维子集. 于是有

(9)

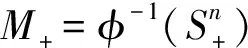
〈x,N〉=〈x,N(x)〉>0 (∀x∈M+)

(10)

由式子(7)和式子(10)， 有

(11)

〈x,N〉=〈x,N(x)〉>0 (∀x∈M-)

(12)

由式子(7)和式子(12)， 可得

(13)

现在， 由式子(6)、 (9)以及式子(12)～(13)， 事实上有

A=B=0

(14)

再次注意到式子(7)、 (9)以及式子(11)、 (13)， 可得

H1Hr-Hr+1=0, ∀x∈M+(∀x∈M-)

(15)

至此， 由式子(15)可知： 在M+和M-的每一点处， 式子(7)的不等式， 事实上都取到了等号.

再由式子(1)中任意一个不等号取到等号的条件， 可得：M+和M-的每一点都是脐点.

最后， 因为Rn+1的坐标原点可以在M所包围的凸区域的内部任意取定， 而且Sn的赤道平面Σn也是可以任意旋转的， 所以M是全脐的.

参考文献：

[1] ALENCAR H, ROSENBERG H, STANTOS W. On the Gauss map of hypersurfaces with constant scalar in spheres[J]. Proceedings of the American Mathematical Society, 2004, 132(12): 3731-3739.

[2] 张远征.Rn+1中常高阶平均曲率超曲面[J]. 数学学报， 2005, 48(4):647-652.

[3] HARDY G, LITLEWOOD J, POLYA G. Inequalities[M]. Cambridge: Cambridge University Press, 1989.

[4] KHO S E. A characterization of round spheres[J]. Proceedings of the American Mathematical Society, 1998, 126(12): 3657-3660.

[5] 王琪. 正曲率空间形式中超曲面的全脐性与高阶平均曲率[J]. 数学学报, 2014, 57(1): 47-50.

[6] 王琪. anti de Sitter 空间中全脐类空超曲面与高阶平均曲率[J]. 山西大学学报(自然科学版), 2016, 39(3): 403-405.

[7] 王琪. de Sitter空间中紧致类空超曲面的全脐性与高阶平均曲率[J]. 安徽大学学报(自然科学版), 2016, 40(1): 7-10.

[8] 王琪. 双曲空间中全脐超曲面与高斯映照像[J]. 浙江大学学报(理学版), 2016, 43(5): 537-538， 549.