（北京理工大学珠海学院 广东珠海 519088）

引言

许多微积分[1]～[5]教材只给出了绕x轴或绕y轴旋转的旋转体体积，这具有局限性。本文研究了绕任意直线y=kx+b和绕极轴旋转的旋转体体积，推导出对应的旋转体积公式。

一、直角坐标系下的旋转体体积

定理1：光滑曲线段y=f(x),x1≤x≤x2绕直线y=kx+b旋转一周所得的旋转体体积为：

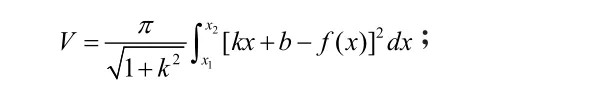
特别地，当k= 0 ,b=0时，

证明：光滑曲线段任意一点(x,f(x))到直线y=kx+b的距离为：

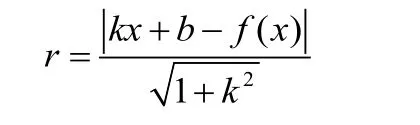
即为旋转曲面横截面的旋转半径，横截面元素的高：

其中θ为该直线的倾斜角。该旋转曲面对应的元素体积为

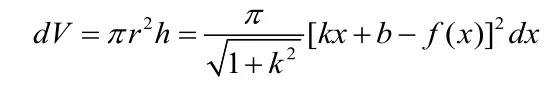
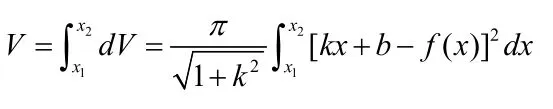
例1 求y=x2与y=x+2围成的图形绕直线y=x+2旋转一周所得的旋转体体积

解：y=x2与y=x+2的交点是(-1,1),(2,4)，由定理1可知，所求旋转体体积

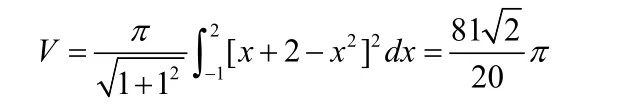
例2[1]求y=x2与y=x+2围成的图形绕直线x=3旋转一周所得的旋转体体积

解：方法一：

y=x2与y=x+2的交点为(-1,1),(2,4)，取典型区间[x,x+dx]，则其对应元素体积可看作长为2π(x+ 2 -x2)，宽为3 -x，高为dx的长方体，由此对应元素体积为dV= 2π(x+ 2 -x2) (3 -x)dx；故

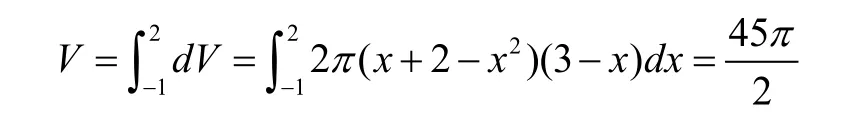
方法二：

y=x2与y=x+2的交点是(-1,1),(2,4)，取典型区间[y,y+dy]，则当0≤y≤1时，对应体积元素为

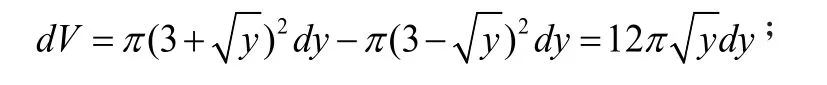
当1≤y≤4时，对应体积元素为

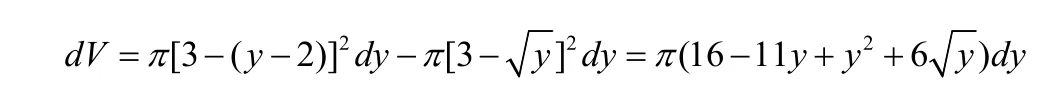
故

二、极坐标系下的旋转体体积

定理2：光滑曲线段r=r(θ) ≥ 0 ,0≤α≤θ≤β绕极轴旋转一周所得的旋转体体积为

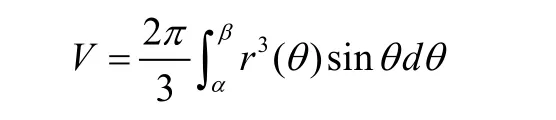
证明：记在[α, θ]的曲边扇形绕极轴旋转一周的体积为V(θ)，则：

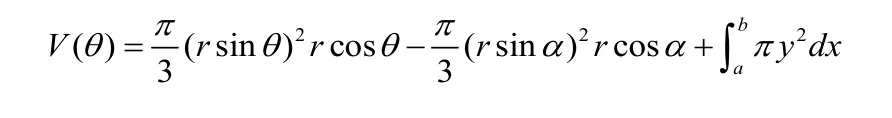
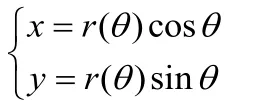
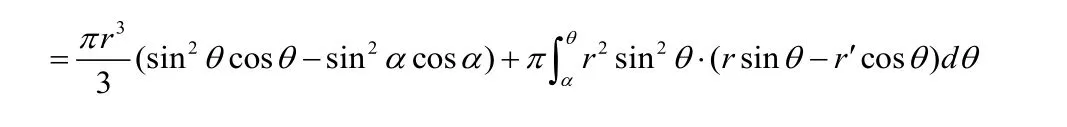
故体积元素

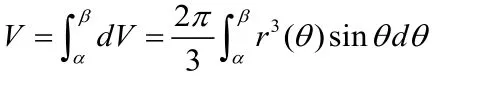
例3 求心形线r=a( 1 - c o sθ) ,0 ≤θ≤π绕极轴旋转一周所得的旋转体体积

例4 求伯努利双纽线r2=a2c os2θ, 0 ≤θ≤π绕极轴旋转一周所得的旋转体体积。

解：由定理2得

[1]贾晓峰,孙洪波,贾云涛.微积分与数学模型(第三版)[M].高等教育出版社,2015.9.

[2]韩云瑞，扈志明.微积分教程[M].清华大学出版社,1999.9.

[3]同济大学数学系.高等数学(第7版)[M].北京:高等教育出版社,2014.7

[4]GerogeBThomas.Thomas’Calculus.(11thEdition).PearsonEducation,2004.

[5]JamesStewart.Calculus(8thEdition).McMasterUniversityandUniv ersityofToronto,2015.