孟献青

(1.山西大同大学数学与统计学院，山西大同 037009;2.山西大同大学量子信息科学研究所，山西大同 037009）

旋转体是指平面图形绕平面内一条直线旋转一周所得的立体。旋转体体积的计算是高等数学定积分应用的一个重要考点，有着非常重要的实际意义。用多种方法研究旋转体体积的计算，不仅有助于提高学生分析问题和解决问题的能力，而且有助于学生把碎片知识一体化，形成更容易接受的知识网。多数教材只介绍了平面图形绕坐标轴旋转所得旋转体的体积，但是局限性比较大。一方面，有些题型虽然可以写出体积表达式，但计算难度比较大，很难求出最终解；另一方面，在实际问题中，平面图形可能绕任意直线进行旋转，所以有必要介绍一下旋转体体积的其他求法，简化计算过程。文中涉及到的定义和术语参见文献[1]。

1 平面图形绕坐标轴旋转

利用元素法求体积微元时，把体积微元近似地看成圆柱体的体积。常规的方法是把体积微元一层一层进行叠加，但是当平面图形绕y轴旋转时，有时按常规方法做起来比较困难，甚至无法求解。通过观察卷纸发现，体积微元也可以一圈一圈进行叠加，这个思想就是柱壳法[2]。

定理1设a,b为常数且0＜a＜b，函数f(x)在闭区间[a,b]上连续，且满足f(x)≥0，则由平面图形a≤x≤b,0≤y≤f(x)绕y轴旋转所形成的旋转体积为V=。

分析平面图形虽然绕y轴旋转，但是不妨对x轴进行分割，小曲边梯形绕y轴旋转就近似地看成小矩形绕y轴旋转，这样就得到一个圆柱壳，即体积微元可近似看成两个小圆柱体的体积差，如图1。

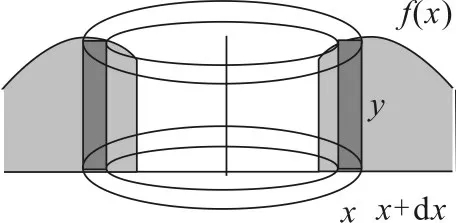
图1 柱壳

证明从[a,b]上任取小区间[x,x+dx]，

ΔV≈π(x+dx)2f(x)-πx2f(x)=2πxf(x)dx+πf(x)(dx)2，

当区间分割很细时，体积元素

dV=2πxf(x)dx，

从而可得旋转体体积为

为了便于理解，也可以把柱壳展开，则柱壳就近似看成长为2πx，宽为dx，高为f(x)的长方体，故长方体的体积为dV=2πxf(x)dx，从而整个旋转体的体积为V=。

例1计算曲线y=sinx(0≤x≤π)和x轴所围图形绕坐标轴旋转所得旋转体的体积。

解（1）绕x轴旋转所得旋转体体积

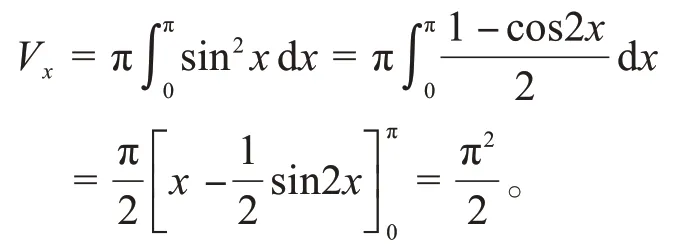
（2）绕y轴旋转所得旋转体体积

方法1（常规方法）绕y轴旋转所得旋转体体积可以看成是曲边梯形OABC绕y轴旋转所得旋转体积减去曲边梯形OBC绕y轴旋转所得旋转体体积的差，如图2。

图2 旋转图形

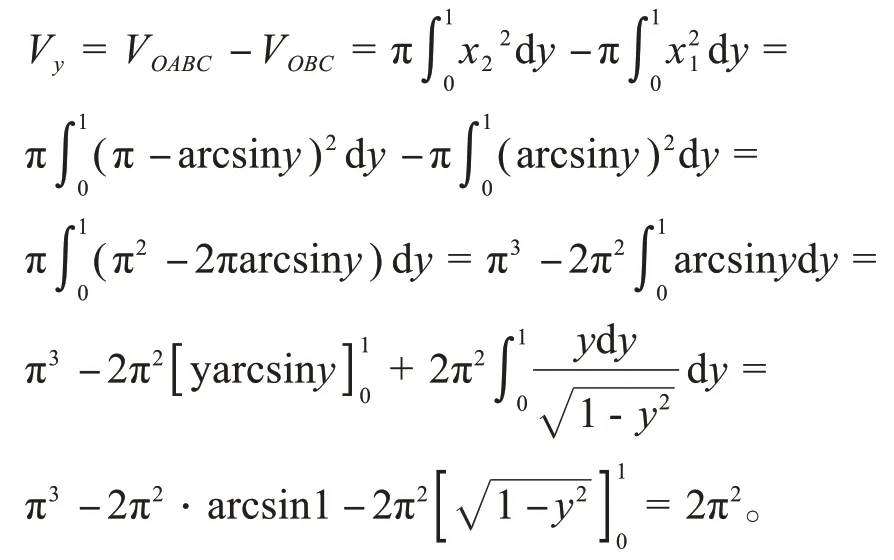
利用常规方法计算绕y轴旋转所得旋转体体积时，涉及到求函数的反函数。有些题目反函数不太容易求解，或者计算难度表较大，所以可以用柱壳法进行计算，以x为积分变量进行计算。

方法2（柱壳法）绕y轴旋转所得旋转体体积可以看成是以2πx为长，以dx为宽，以sinx为高的长方体的体积，所以

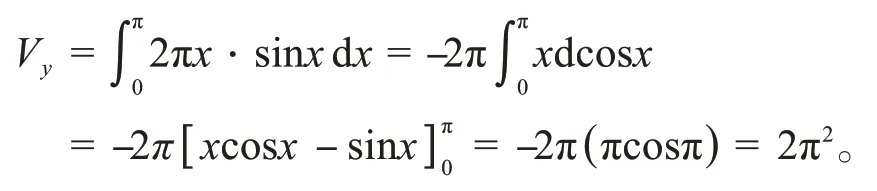
在计算旋转体体积时，是选用常规方法还是柱壳法，与旋转体的形状有关。一般情况下，如果曲边梯形绕x轴旋转，用常规方法计算旋转体的体积；若曲边梯形绕y轴旋转，则利用柱壳法相对简单。从定理中1很容易得到绕平行于y轴的直线旋转所得旋转体的体积。

推论1设f(x)在[a,b]上连续，且f(x)≥0，则平面图形a≤x≤b,0≤y≤f(x)绕直线x=x0旋转所得旋转体的体积为：

（1）当x0≤a时，

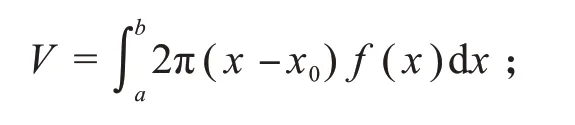
（2）当x0≥b时，

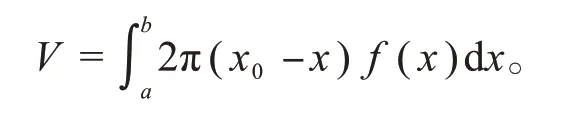
例2求y=x2,y=x所围成的图形分别绕y轴，直线L1:x=-1 和L2:x=2 旋转一周所得旋转体的体积。

解联立方程，可得交点坐标为（0,0），（1,1），由柱壳法得，绕y轴旋转所得旋转体体积为：

由推论1 知，绕直线x=-1 旋转所得旋转体体积为：

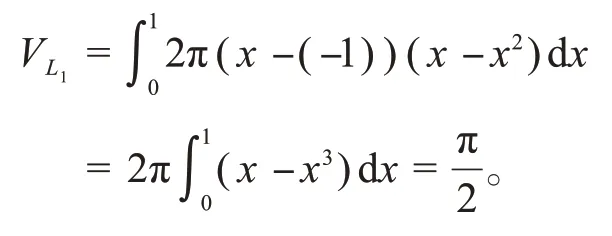
绕直线x=2旋转所得旋转体体积为：

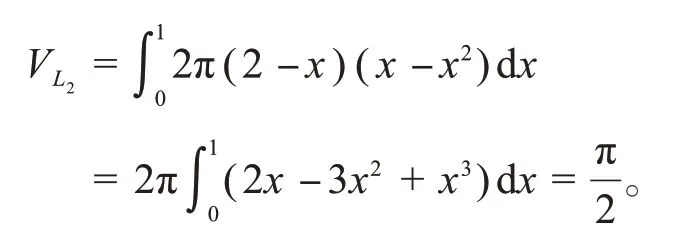
2 平面图形绕任意直线y=kx+b旋转

定理2由光滑曲线段y=f(x)，a≤x≤b与直线y=kx+b所围平面图形绕直线y=kx+b旋转一周所得旋转体的体积为：

证明旋转曲面的横截面半径可以看成是光滑曲线段任意一点(x,f(x))到直线y=kx+b的距离d=；

横截面对应的高为：

h=，其中θ为直线y=kx+b的倾斜角。故体积元素为：

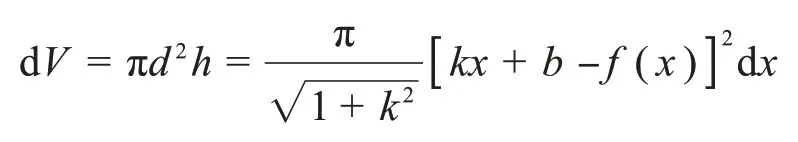
从而旋转体体积为：

当k=0,b=0 时，可得绕x轴旋转所得旋转体体积。

例3求y=x2,y=x所围成的图形绕直线y=x旋转一周所得旋转体的体积。

解交点坐标为(0,0),(1,1)，且k=1,b=0,f(x)=x2，由定理2 可知，所得旋转体体积为：

3 利用Pappus定理计算旋转体的体积

古希腊数学家Pappus 总结出了特殊旋转体体积的计算公式，尤其当平面图形为对称图形时，计算起来特别简便。

定理3设D是与直线l不相交的平面闭区域，面积为S。D的形心到直线l的距离为d，则平面图形D绕直线l旋转一周所得旋转体体积为Vl=2πdS[4]。

例4求圆x2+(y-1)2=1 绕直线y=x-1 旋转一周所得旋转体的体积。

解由对称性知，圆的形心坐标为(0,1)，故由点到直线的距离公式知，形心(0,1)到旋转轴y=x-1 的距离为：

又圆的面积为π，所以由Pappus 定理知，旋转体的体积为V=。

所以当平面图形内部与旋转轴没有交点时，求旋转体的体积可以转换成求平面图形的面积及形心到旋转轴的距离，利用Pappus定理进行计算。

4 结论

利用元素法讨论了平面图形绕坐标轴及任意直线旋转所得旋转体的体积，当平面图形绕y轴旋转时，用常规方法及柱壳法两种方法进行解题，并对比了两种方法的优劣；对于形心坐标比较好计算的平面图形绕直线旋转所得旋转体的体积，可以利用Pappus 定理，转化为计算平面图形的形心到直线的距离和平面图形的面积进行计算，从而可以简化计算过程。