李小艳　陈绍平

(武汉理工大学理学院　武汉 湖北 430000)

0　引　言

随着计算机运行速度的提高和逆向工程的快速发展，从20世纪90年代中期起，B样条曲线曲面拟合一直是CAGD领域的研究热点，也是CAGD领域的经典问题之一[1]。B样条具有几何变换不变性、局部支撑性、凸包性、变差缩减性等诸多优良性质，这使得它成为形状数学描述的主流方法，并广泛应用于数据可视化与逼近、医学图像轮廓重构和几何建模等领域[2]。

解决B样条曲线曲面拟合问题的关键在于B样条节点矢量和控制顶点的选取，合适的节点矢量与控制顶点能保证拟合曲线的光滑度和拟合效果。把节点矢量和控制顶点均视为变量时，拟合问题就变为一个多维多变量高度非线性的最优化问题。解决该问题的方法大致可以被分为三类：传统的节点插入和节点删除方法、支配点和特征点方法以及人工智能算法。传统的方法一般是将节点向量进行固定，得到一个关于控制顶点的线性系统，但是这些方法并不能处理带有不连续点、尖点和拐点的复杂型曲线。支配点和特征点方法是通过提取数据点的形状信息(包括拐点、折痕点和曲率极值点等)用于节点的选择，但是这些方法往往仅限于连续曲线。近年来，利用人工智能算法求解并优化B样条拟合问题受到诸多学者的关注。如Yoshimoto等[3]提出了一种实数编码的遗传算法对平面曲线进行拟合，该方法能自动的确定节点的数量和位置，不仅可以处理光滑的数据拟合问题，也可以处理带尖点和不连续点的数据拟合问题；周明华等[4]采用遗传算法同时对数据点的参数化和节点矢量进行优化，与传统方法相比取得了较高的拟合效果；穆国旺等[5]提出一种改进的遗传算法，将误差精度考虑在内，实现了在给定误差下能使用最少的控制顶点进行B样条曲线拟合，但是该方法的运算时间较长；Adi等[6]采用粒子群优化(PSO)方法进行NURBS曲线拟合，该方法将控制顶点作为待求解的变量，但是误差比较大；Galvez等[7]利用PSO通过固定节点个数自适应的确定节点的位置优化拟合曲线；Ulker等[8]提出将人工免疫算法(AIS)应用于求解B样条曲线拟合问题上，得到较好的结果；Zhao等[9]在B样条曲线逼近问题中采用了一种新颖的随机优化方法，利用高斯混合模型和聚类技术来实现自适应节点配置，但该方法仅对封闭曲线进行了拟合实验。何兵朋等[10]对差分进化算法的变异操作进行改进，设计出一种新的B样条曲线拟合方法。近几年，许多学者也不断的对这些智能算法进行改进来改善B样条拟合效果。如Trejo-Caballero G 等[11]设计出一种分层编码方法，将节点与控制顶点分别进行二进制编码和实数编码，利用遗传算法进行拟合，得到了较好的拟合效果。

在文献[13]中，他们对DE、PSO和EA在处理数值优化问题时的表现进行了评估，与其他方法相比，DE展示出了较高的优越性。因此本文在诸多学者研究的基础上，将一种改进的自适应差分进化算法应用于解决B样条曲线曲面最小二乘拟合问题。此方法采用了DE/current-to-best/的变异策略和带有随机游走(Random Walk)的交叉操作，利用随机游走的随机机制弥补DE/current-to-best/容易早熟收敛的缺陷。同时为了跳出局部最优解，利用混沌系统的随机性与遍历性设计出一个针对当前种群最优解的局部搜索操作，有效地平衡了DE的开发能力和探索能力。新的差分进化算法在进行B样条曲线曲面拟合时能够根据数据点分布特征配置内节点的位置，并在需要时产生多重节点。试验结果表示，与标准的差分进化算法相比，用本文的方法得到的B样条曲线曲面逼近精度更高。

1　B样条曲线的最小二乘拟合

(1)

式中：j=0,1,…,M-1;xj=[a,b]，f(x)为采样函数(对于散乱数据来说，f(x)是未知的)，ε为噪声误差，N为采样数量，n为内节点个数，[a,b]为拟合区间。k次B样条目标曲线为：

(2)

(3)

式中：pi(i=0,1,…,n+k)为控制顶点，Ni,k(x)(i=0,1,…,n+k)为由de-Boor递推公式定义的k次B样条基函数(本文选择三次B样条曲线)：

‖·‖是欧氏距离。端节点设置为k+1重节点：u0=u1=…=uk,un+k+1=un+k+2=…=un+2k+1对于一组固定的内节点，采用标准的最小二乘技术，欲使式(3)中的Q达到最小，应使它关于n+k-1个控制顶点的导数为0，于是就得到了n+k-1个以pi(i=1,2,…,n+k-1)为未知量的线性方程组：

(NTN)P=NTR

(4)

这里N是(M-2)×(n+k-1)的标量矩阵：

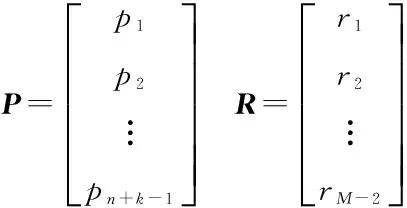
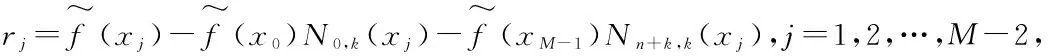
2　差分进化算法原理

差分进化算法DE(Differential Evolution)与其他遗传类型算法相似，以迭代的方式对种群中个体进行变异、交叉和选择操作直到根据适应度函数找出最佳个体。标准的DE算法描述如下：

2.1　差分变异操作

变异就是指从当前种群中随机选择几个个体得到差分矢量乘上变异系数作用于目标个体对其产生扰动，生成变异个体。五种最常用的差分变异策略如下：

DE/current-to-best/:

(5)

2.2　交叉操作

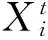
式中：CR∈[0，1],rand1(0,1)为均匀分布的随机数，jrand为介于1到D的随机整数下标索引，可以确保试验个体中至少有一个基因是由变异个体贡献的。

2.3　选择操作

DE根据个体的适应度函数值对目标个体和试验个体进行贪婪选择，以最小化问题为例，具体操作如下：

(6)

3　改进差分进化算法的B样条拟合

(1) 差分变异操作。选择式(5) DE/current-to-best/的变异策略，该策略具有局部搜索能力强，收敛速度快的优点，但全局搜索能力较弱，容易陷入局部最优。缩放因子F由下式决定：

(2) 交叉操作。算法早熟收敛是因为随着DE的进化，种群中个体渐渐聚集，差异减小。为了避免局部最优，本文借鉴文献[19]中的带有随机游走的交叉操作，随机游走是一个可以向任何方向前进的、到达任何位置的无规则运动，这种随机性机制在用于DE搜索过程时可以增加种群的多样性，有效避免早熟现象。交叉操作的表达式如下：

(7)

交叉概率CR和参数RW的表达式如下：

在DE中差分矢量缩放因子F和交叉概率CR对优化性能有着重要的影响。Storn等[15]建议过参数的选取范围应为:F∈[0.5,1]、CR∈[0.8,1]，本文对参数的设置符合这个条件。

(3) 混沌局部搜索操作。设计出一种混沌局部搜索操作，在当前最优个体的邻域范围内搜索更优解，以跳出局部最优。通过一维Logistic映射生成混沌序列，迭代公式如下：

Zi+1=μZi(1-Zi)i=0,1,2,…

(8)

(9)

式中：λ为局部搜索系数，针对不同的实例λ取不同的值。若在搜索结果中找到了优于当前代最优个体的内节点向量，则对其进行取代。

(4) 适应度函数。使用统计学中贝叶斯信息准则BIC[23]作为适应度函数，表达式为：

BIC=M×(lnQ)+(lnM)×(2n+k+1)

(10)

式中:M为数据点数量，Q为由式(3)计算所得的残差平方和，n+k+1代表控制顶点个数，n代表内节点个数。适应度函数值越小，代表找到的节点矢量越优，拟合误差越小。

在B样条曲线拟合问题中，节点数量是变化的，控制顶点的个数也会随之改变，如果控制顶点太少，无法还原出原数据点分布特征，拟合误差就会增大；控制顶点太多，拟合曲线的光滑度会降低。因此如果只以残差平方和Q为目标函数，就会忽略模型复杂度和控制顶点个数对曲线几何形状的影响。选取BIC为适应度函数，它的第一项能够保证模型函数的精度，第二项添加了对模型函数自由参数个数的惩罚，通过精度与计算复杂度之间的平衡，获得最优的逼近模型。BIC的另一个优势在于它避免了使用主观参数(如误差界限和平滑因子)来判断拟合模型。

基于该算法的三次B样条曲线拟合流程如下：

输出：最佳内节点。

Step2利用式(8)求出种群中每个内节点个体的适应度值，获得最优个体及其对应的适应度值。

Step3判断迭代是否达到Tmax，若是，退出，否则执行下一步。

Step4对种群中个体根据式(5)和式(7)进行变异和交叉操作。

Step5按照式(6)进行选择操作，生成新一代个体，令t=t+1。

Step6判断种群是否陷入局部最优，若是，则根据式(8)和式(9)进行混沌局部搜索，更新种群中最优个体。若否，返回Step2。

4　仿真实验与分析

为了验证本文算法在解决B样条曲线曲面最小二乘拟合问题上的有效性，选择5个测试函数进行试验分析。

4.1　曲线拟合

所有曲线拟合的试验中，采样数据点均由测试函数根据式(1)得到，噪声误差εj取均值为0，方差为1的标准正太分布随机数。差分进化算法的参数均设置为种群规模NP=100，最大迭代次数Tmax=200，由于本文实验拟合区间均为[0,1],局部搜索系数我们取较小的值λ=0.025。对于每一个测试函数我们都在取值范围内选取M=201个数据点，试验在同等条件下重复30次。

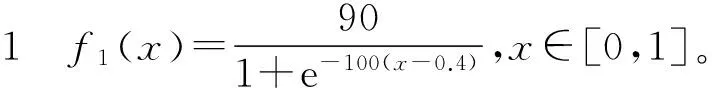
该函数是多峰值的分段函数，x=0.6是它的不连续点。

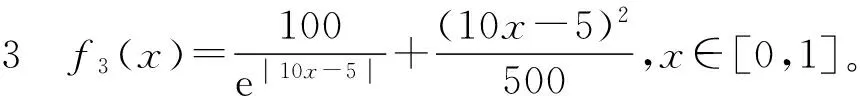
图1(a)、图2(a)、图3(a)分别为本文算法对取自函数f1(x)、f2(x)、f3(x)的数据点进行试验得到的BIC值与内节点数之间的关系，从图中可以得到f1(x)、f2(x)、f3(x)对应的最佳拟合内节点个数分别为4、8、5。图1-图3中的(b)显示了BIC值与残差平方和Q的变化情况，实线表示适应度BIC，虚线表示残差平方和Q；图1-图3中的(c)分别绘出了例1-例3由最佳内节点得到的最佳拟合效果图，三角形标出了最佳内节点的位置，×是拟合数据点，实线是B样条拟合曲线。

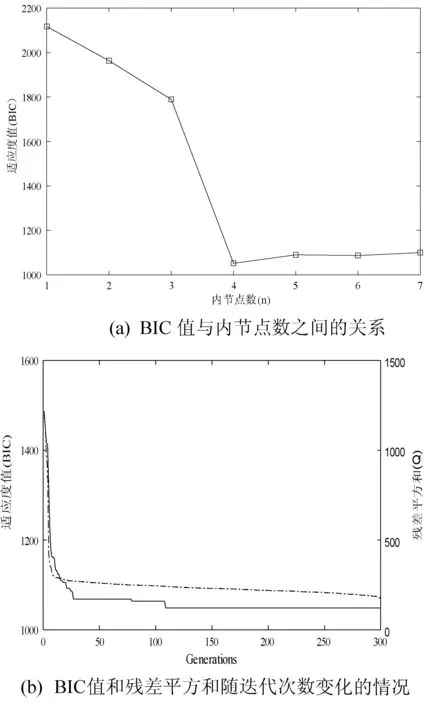
图1　例1函数拟合结果

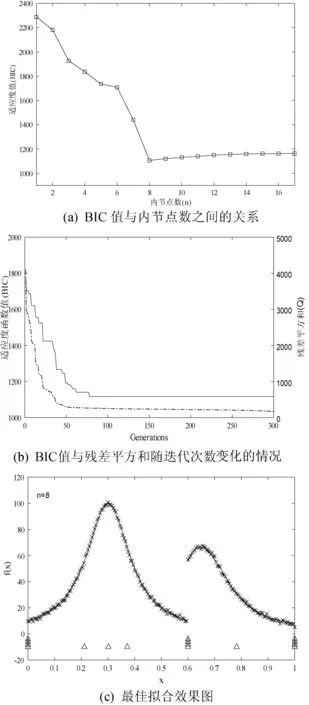
图2　例2函数拟合结果

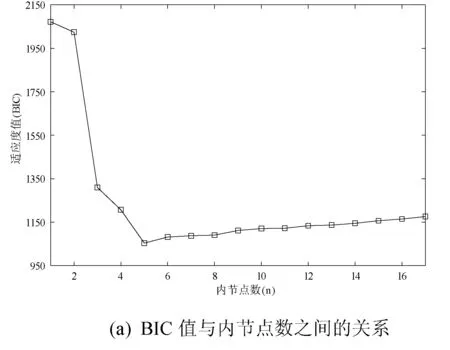
图3　例3函数拟合结果

图1(b)、图2(b)、图3(b)为本文算法对例1-例3进行拟合过程中随着迭代次数的增加，最佳个体的适应度值和残差平方和的变化曲线。从图中可以看出，对于每一个测试函数，适应度值基本都在在100代左右收敛，说明我们的算法收敛速度快且结果稳定。图1-图3中(c)对应例1-例3的拟合效果图与文献[3,10,12]中的拟合结果一致，并且拟合效果较好。必须说明的是对于三次B样条曲线，如果某个内节点的重复度为4，就说明该三次B样条曲线在该点处是不连续的，函数f2(x)的拟合结果就说明了这种情况。这表示本文的算法能够根据数据点的分布特征来自动分配节点位置，使拟合结果与数据点的分布特征一致。三个拟合效果图可以说明本文算法不仅能够较好地拟合如例1这种在某点处发生突变的光滑曲线，也能够处理例2、例3这种带有间断和尖点的情况。例2的函数图像在x=0.6处发生间断，我们的方法相应的在该点处产生了四重节点，根据B样条曲线的性质，拟合曲线在x=0.6处也发生了间断。

将传统的带五种不同变异操作的差分进化算法分别与本文方法进行比较。进行30次试验，表1、表2给出的是在相同节点数量的情况下对应于例1-例3的试验结果，总结的是30次试验的最小、最大以及平均的适应度值(BIC)和残差平方和(Q)。从表1、表2中可以看出，由本文方法找到的最佳节点矢量对应的适应度值(BIC)和残差平方和(Q)都比传统的差分进化算法更小。这说明我们的方法在处理B样条曲线最小二乘拟合时，拟合效果更好、拟合精度更高。

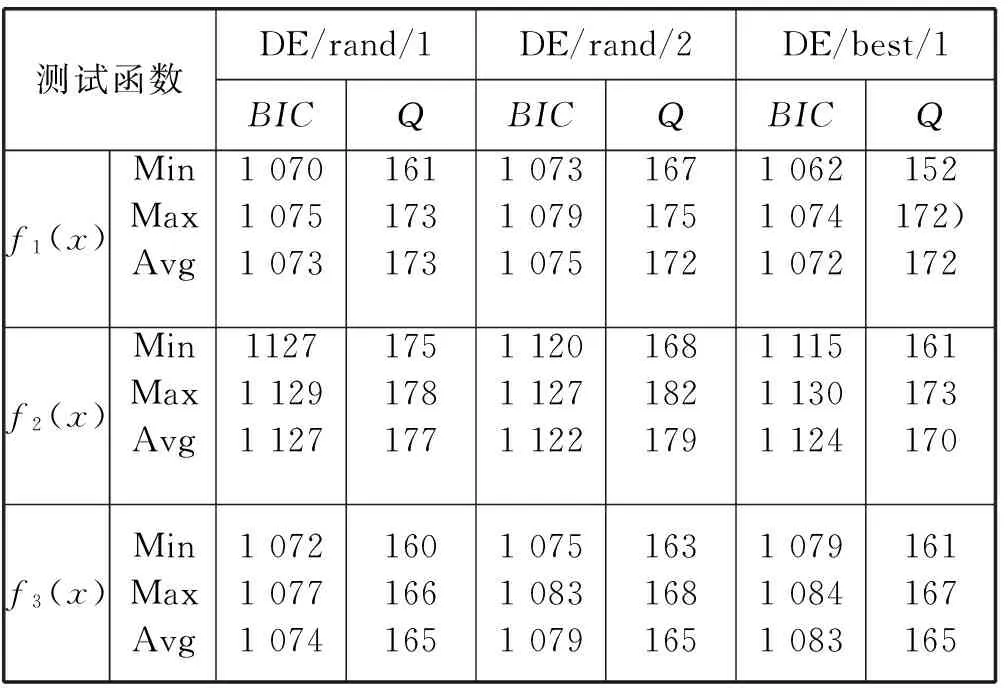
表1　传统差分进化算法与本文算法的比较

表2　传统差分进化算法与本文算法的比较

4.2　曲面拟合

将本文的算法延伸到曲面拟合问题上，以例4、例5为测试函数选取双三次B样条曲面进行拟合数值试验。试验均将拟合区域0≤x≤1、0≤y≤1分别32等分，进行数据点的直接采样(无噪声)；算法参数均设置为NP=50、Tmax=200。取平均平方误差MSE为适应度函数，定义如下：

式中:S(x,y)为拟合曲面，f(x,y)为采样函数。

式中:x,y∈[0,1]。该函数为带尖点的曲面。

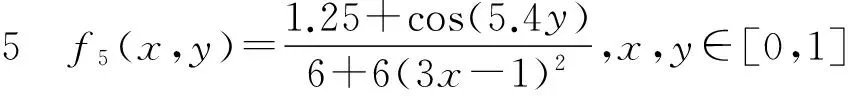
图4-图7分别为根据例4和例5函数解析式直接用Matlab绘制的图形和用本文算法绘制拟合曲面图形的对比图。由图可知，使用本文算法得到的双三次B样条拟合曲面几乎能准确构造出采样数据的原始图像。多次试验的数据显示，对于测试函数4，大约迭代到第10～20次，平均平方误差就已达到10-6，最终收敛到10-8，最佳内节点个数为8×8。对于测试函数5，迭代到第10代左右，平均平方误差达到10-9，最终收敛到10-12，最佳内节点个数为5×5。这说明本文的算法收敛速度快，拟合精度高。

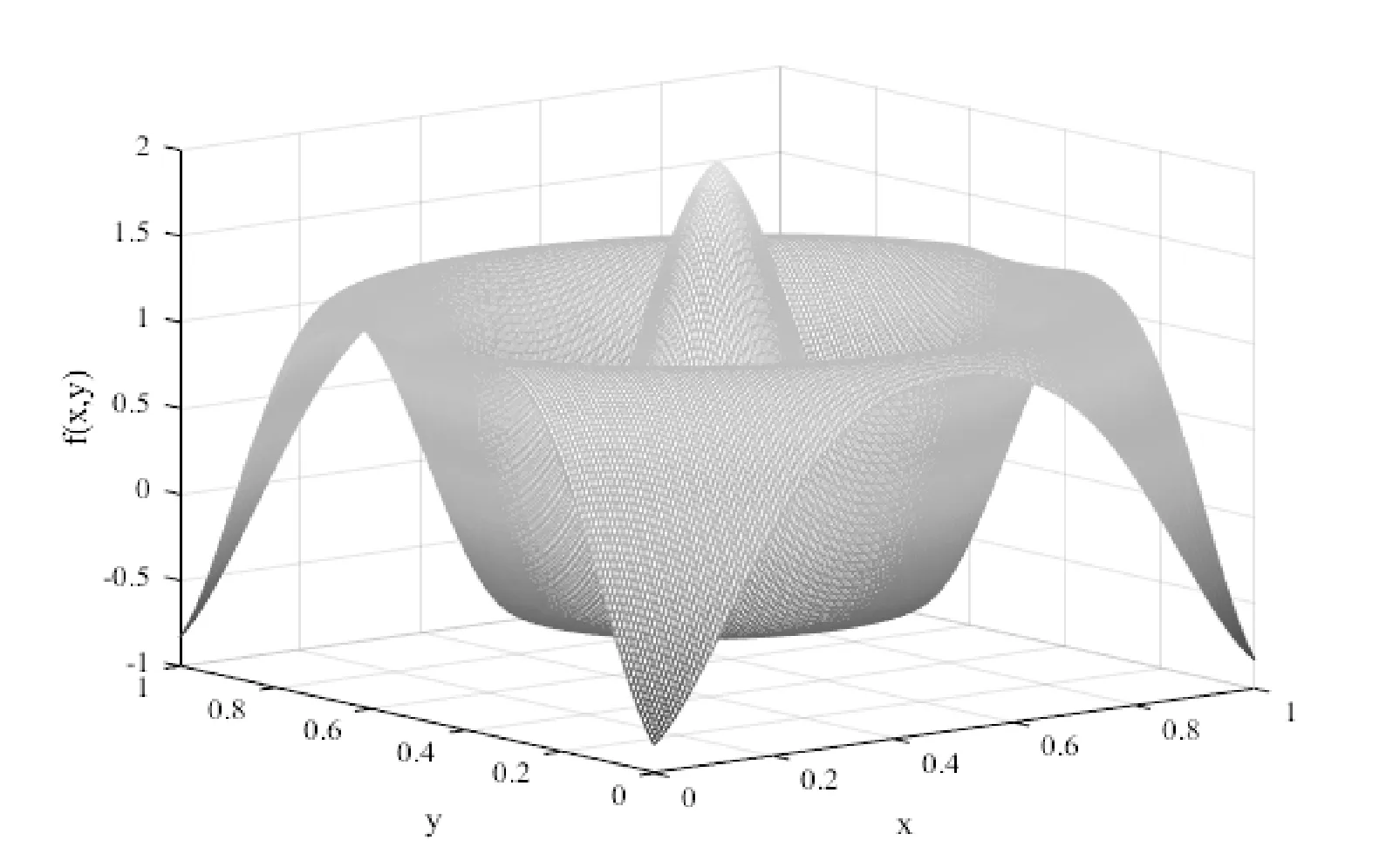
图4　例4的根据函数解析式绘制的原图

图5　例4的本文算法的拟合效果图

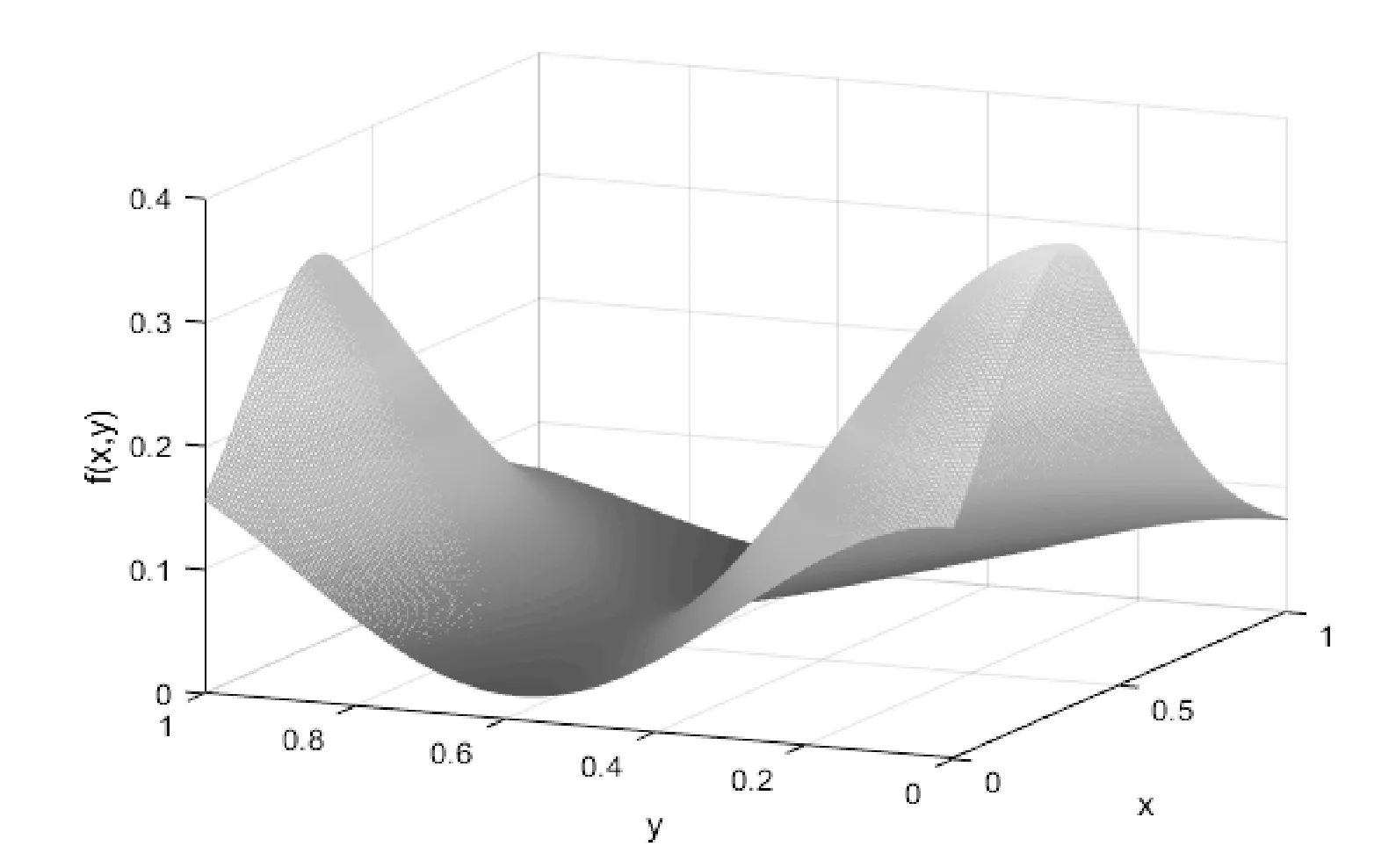
图6　例5的根据函数解析式绘制的原图

图7　例5的本文算法的拟合效果图

5　结　语

本文基于差分进化算法在处理数值优化问题时所表现出的收敛速度快、求解精度高的优势，将差分进化算法进行改进，应用于B样条曲线曲面的最小二乘拟合问题。该方法选择带有随机游走的交叉操作来克服DE/current-to-best易早熟收敛的缺点；并且设计出一种带有混沌系统的局部搜索操作来跳出局部最优解。将该方法与传统的差分进化算法进行比较，试验数据以及效果图显示，该方法在处理带间断和尖点的数据时能够自适应地确定节点的位置，并且与传统的差分进化算法相比在拟合误差精度上也有显著的提高。其不足之处有两点：首先，本文方法并没有完全自适应地同时确定节点的数量与位置，这主要是受限于差分进化算法的变异操作不允许我们将节点矢量设置为变长度的个体。其次，由于B样条曲线和曲面不能精确地表示除抛物线外的二次曲线圆弧、和除抛物线面外的二次曲面，出于工业实际(特别是飞机外形的设计)精确表示二次曲线弧和二次曲面的需要，因此需要我们进一步研究有理B样条的曲线曲面拟合问题。鉴于此，作者将进一步研究差分进化算法的改进，解决B样条曲线曲面最小二乘拟合问题，实现节点数量和位置对不同实例的自适应调整，并研究有理B样条的曲线曲面拟合问题。

[1] 施法中. 计算机辅助几何设计与非均匀有理B样条[M].北京:高等教育出版社, 2013:301-336.

[2] Piegl L, Tiller W. The NURBS Book[M]. Berlin: Springer-Verlag, 1995.

[3] Yoshimoto F, Harada T, Yoshimoto Y. Data fitting with a spline using a real-coded genetic algorithm[J]. Computer-Aided Design, 2003, 35(8):751-760.

[4] 周明华，汪国昭. 基于遗传算法的B样条曲线和Bezier曲线的最小二乘拟合[J]. 计算机研究与发展, 2005, 42(1):135-143.

[5] 穆国旺, 臧婷, 赵罡. 用改进遗传算法确定B样条曲线的节点矢量 [J]. 计算机工程与应用, 2006,42(1):88-90.

[6] Adi D I S, Shamsuddin S M, Ali A. Particle Swarm Optimization for NURBS Curve Fitting[C]// Sixth International Conference on Computer Graphics, Imaging and Visualization. IEEE Computer Society, 2009:259-263.

[7] Gálvez A, Iglesias A. Efficient particle swarm optimization approach for datafitting with free knot B-splines[J]. Computer-Aided Design, 2011, 43(12):1683-1692.

[8] ülker E, Arslan A. Automatic knot adjustment using an artificial immune system for B-spline curve approximation [J]. Information Sciences, 2009, 179:1483-1494.

[9] Zhao X, Zhang C, Yang B, et al. Adaptive knot placement using a GMM-based continuous optimization algorithm in B-spline curve approximation [J]. Computer-Aided Design, 2011, 43:598-604.

[10] 何兵朋, 冯仁忠, 余胜蛟. 基于差分进化算法的B样条曲线曲面拟合[J]. 图学学报, 2016, 37(2):178-183.

[11] Trejo-Caballero G, Rostro H, Garcia-Capulin C H, et al. Automatic Curve Fitting Based on Radial Basis Functions and a Hierarchical Genetic Algorithm[J]. Mathematical Problems in Engineering, 2015, 2015(731207).

[12] Han X, Quan L, Xiong X, et al. Diversity enhanced and local search accelerated gravitational search algorithm for data fitting with B-splines[J]. Engineering with Computers, 2015, 31(2):215-236.

[13] Vesterstrom J, Thomsen R. A comparative study of differential evolution, particle swarm optimization, and evolutionary algorithms on numerical benchmark problems[C]// Evolutionary Computation, 2004. CEC2004. Congress on. IEEE, 2004:1980-1987.

[14] Storn R, Price K. Differential evolution: a simple and efficient heuristic for global optimization over continuous spaces[J]. Kluwer Academic Publishers, 1997, 11(4):341-359.

[15] Storn R, Price K. Differential evolution: a fast and simple numerical optimizer[C]//1996 Biennial Conference of the North American Fuzzy Information Processing Society. New York, 1996:524-527.

[16] Tanabe R, Fukunaga A. Success-history based parameter adaptation for differential evolution[C]// IEEE Congress on Evolutionary Computation, 2013:71-78.

[17] Das S, Abraham A, Chakraborty U K, et al. Differential evolution using a neighborhood-based mutation operator[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(3):526-553.

[18] Cui L, Li G, Lin Q, et al. Adaptive Differential Evolution Algorithm with Novel Mutation Strategies in Multiple Sub-populations[J]. Computers & Operations Research, 2015, 67:155-173.

[19] Zhan Z H, Zhang J. Enhance Differential Evolution with Random Walk [C]// Conference Companion on Genetic & Evolutionary Computation, 2012:1513-1514.

[20] Li G H, Lin Q Z, Cui L Z, et al. A novel hybrid differential evolution algorithm with modified CoDE and JADE[J]. Applied Soft Computing, 2016, 47:577-599.

[21] Liu G, Xiong C Q, Guo Z L. Enhanced differential evolution using random-based sampling and neighborhood mutation[J]. Soft Computing, 2015, 19:2173-2192.

[22] Cai Y, Zhao M, Liao J. Neighborhood guided differential evolution[J]. Soft Computing, 2016:1-44.

[23] Schwarz G E. Estimating the dimension of a model[J]. Annals of Statistics, 1978, 6(2):461-464.