郭宇红 张 伟 杨晓东

(北京工业大学 机电学院, 北京 100124)

引言

随着高新技术的发展,人们已不再满足于材料单纯的轻质化,而是寻找兼有轻质化和其他某种或几种优良性能相结合的先进材料以适应不同的需求,作为一种生物材料中普遍存在的典型结构,多孔介质在自然界动植物体中发挥着不可替代的生理功能. 在这些构型中,3D-Kagome结构拥有更加稀少的杆件布局和更小的相对密度.3D-Kagome结构是由两个正四面体对顶连接而成的网架结构,将这种核心连接在面板上就形成了3D-Kagome点阵夹芯板[1-3]. 通过实验和数值模拟得到结论,相对于其他构型的点阵夹芯板,在同一相对密度情况下,3D-Kagome点阵夹芯板具有更高的强度和抗屈曲性能[4-6]. 此外,3D-Kagome点阵夹芯板在功能性方面的表现也比较突出,例如具有优异的驱动和致动性能,能够在受到很小的内部抵抗力的情况下获得很大范围内的整体变形. 点阵材料在航空航天等领域有着广泛的应用,可以减轻飞行器的重量,同时保证结构的强度和刚度满足要求.

自从上世纪70年代,Golubitsky、Schaeffer和Stewart等将奇异性理论和群论方法引入分叉问题的研究后,分叉理论得到了越来越多的关注,从而也推动了奇异性理论的发展.1981年,Golubitsky和Langford[7]研究了退化Hopf分叉问题的分类和开折.1982年,Golubitsky[8]和Martinet[9]等讨论了在强等价下光滑映射芽的开折,给出了各种形式的通有开折定理.1985年,Golubitsky和Schaeffer[10]得到了余维数不大于3的分叉问题的分类,其中状态变量只有一个且具有Z2对称性. 1986年,Keyfitz[11]给出了余维数不大于7的分叉问题的分类,其中状态变量只有一个但不具对称性,给出了各种形式的通有开折定理,但是这些研究都是针对单状态变量、单分叉参数的分叉系统而言. 随后人们将奇异性理论推广到了多状态变量的分叉研究中,1986年,Golubitsky[12]研究了单参数两状态变量余维数不超过2的分叉问题的分类,其中状态变量关于二面体群4D对称,1988年,Melbourne[13]得到了单参数三个状态变量余维数不超过1的分叉问题的分类.

在开始的研究中,研究工作没有考虑分叉参数的对称性. 1986年,Gaffney[14]将幂单代数群和幂零Lie代数应用于多参数分叉问题中,给出了D(Γ)-等价. 1996年,Furter和Sitta[15]等考虑了分叉参数的对称性,研究了余维数不大于1的分叉问题的分类.2003年,高守平和李养成等[16]讨论了状态变量和分叉参数具有不同对称性的余维数不超过1的分叉问题的分类,其中状态变量关于二面体群D4对称,分叉参数关于S1对称. 2006年,郭瑞芝[17]给出了状态变量和分叉参数具不同对称性的岔问题的分类及识别条件,其中状态变量关于二面体群D3对称,分叉参数关于O(2)对称. 2007年,崔登兰和李养成等[18]也研究了含有两组状态变量且参数具有对称性的等变分叉问题.

随着研究的进一步深入,开始了多分叉参数的研究工作. 1993年,Lavassani等[19]通过奇异性理论研究了等变多参数分叉,给出了多参数分叉问题的有限确定定理和正规型,并讨论了多参数分叉的稳定性问题. 2000年,胡凡努和李养成[20]将状态变量分为两组,一组状态变量可以独立变化,而另一组状态变量则依赖于前一组状态变量,研究了该类分叉问题的通有开折.2003年,高守平和李养成[21]研究了多参数等变分歧问题及其开折,给出了通有的开折定理. 但是人们通常将分歧(分叉)问题中的状态变量看作是“平等”的,并不加以区分. 2005年,郭瑞芝和李养成[22]研究了含有两组状态变量的多参数等变分歧问题在左右等价群下的开折,得出了通有开折的充要条件. 2010年,秦朝红和陈予恕等[23-26]研究了含有两个状态变量和两个分叉参数的分叉系统的奇异性理论,并给出了含有两个分叉参数系统的转迁集的计算方法.

本文以点阵夹芯板为切入点,计算1:1内共振情况下点阵夹芯板的非线性动力学方程,推广含有两个状态变量和三个及三个以上参数的一般非线性动力学分叉方程的奇异性理论,利用推广的奇异性理论计算复合层合板的非线性动力学分叉方程的普适开折,同时计算普适开折的转迁集,并进一步讨论若干重要参数对稳定性的影响.

1点阵夹芯板非线性动力学分叉方程的普适开折

1.1 点阵夹芯板的非线性动力学方程

考虑横向激励与面内激励联合作用下四边简支点阵夹芯板,在板的中面上建立坐标系oxy,板在x和y方向的长度分别为a和b,厚度为h,设夹芯板中面上任一点在x、y和z方向的位移分别为u、v和w,板承受沿z方向的横向激励f=F(x,y)cosΩ1t与沿y方向作用于x=0和x=a的面内激励p=p0+p1cosΩ2t联合作用,这里,Ω1和Ω2分别为横向激励与面内激励的频率. 点阵夹芯板由点阵夹芯层与覆盖在上面的两层蒙皮组成,蒙皮采用各向同性材料,其厚度为hf,芯层厚度为hc. 其动力学方程为:

(1a)

(1b)

其中,w1为第一阶模态的振幅,w2为第二阶模态的振幅,μ1和μ2表示对应于两阶模态的阻尼,F1和F2表示对应于两阶模态的横向激励幅值,βij(i=1,2;j=1…7)表示材料参数. 方程(1)的详细推导过程及其所有参数表达式参见文献[27].

1.2 在1:1内共振情况下点阵夹芯板动力学方程摄动分析

利用多尺度法进行研究,将方程(1)中的阻尼项、参数激励项、热激励项和非线性项添加小扰动项ε,考虑点阵夹芯板的主参数共振-1:1内共振的情况,共振关系如下:

2ω1=Ω1-εσ1,2ω2=Ω2-εσ2, Ω1=Ω2

(2)

式中ω1和ω2为相应线性系统的第一阶和第二阶固有频率,σ1和σ2为系统的调谐参数,为了方便处理,令Ω1=1.

设方程(1)的一致渐近解为:

w(x,t,ε)=w0(x,T0,T1)+εw1(x,T0,T1)

(3)

其中T0=t,T1=εt.

则有微分算子:

(4a)

(4b)

将式(3)和(4)带入方程(1)中,比较方程两边摄动参数ε同阶次的系数,得到如下方程:

ε0阶:

(5a)

(5b)

ε1阶:

(6a)

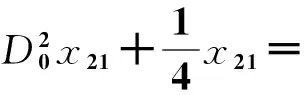
(6b)

方程(5a)和(5b)的解可以写成如下复数形式:

(7)

将方程(7)代入方程(6a)和方程(6b)中得到:

(8a)

(8b)

其中cc和NST分别表示方程(8)右端函数的复数部分和长期项.

A1和A2可以表示为下列形式:

(9)

消除方程(8)中可以产生长期项的部分,将方程(9)代入方程(8), 将实部与虚部分离,得到极坐标形式的四维平均方程为:

(10a)

(10b)

(10c)

(10d)

(11b)

展开方程(11),得到:

(12a)

(12b)

式中:

k19=-β13cos(φ1-φ2),k110=-β13β16cos(3φ1-φ2),

k111=-3β14β16cos(2φ1),k112=-3β14,

k116=2β16sin(2φ1),k117=2β16cos(2φ1),

k29=-β23cos(φ2-φ1),k210=-β23β26cos(3φ2-φ1),

k211=-3β24β26cos(2φ2),k212=-3β24,

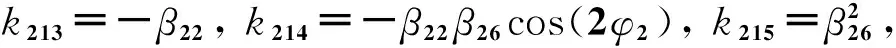
k216=2β26sin(2φ2),k217=2β26cos(2φ2)

(12c)

1.3 在1:1内共振情况下点阵夹芯板动力学方程分叉分析

令:

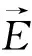
(13)

式中:

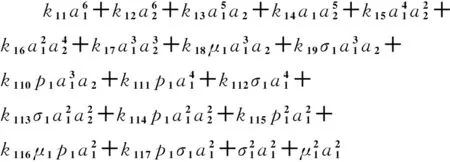
(14a)

(14b)

z=(a1,a2),λ=(σ1,σ2,p1)

(14c)

1.3.1限制切空间

定理1.1芽g(z,λ)的限制切空间RT(g,1)能够表示为:

RT(g,1)=M2+M〈σ1,σ2,p1〉

(15)

证明:根据命题1.4(文献[10]中,第二册169页),RT(g,1)的生成元有14个:

(g1,0),(g2,0),(0,g1),(0,g2),a1(g1,a1,g2,a1),

a2(g1,a1,g2,a1),σ1(g1,a1,g2,a1),σ2(g1,a1,g2,a1),

p1(g1,a1,g2,a1),a1(g1,a2,g2,a2),a2(g1,a2,g2,a2),

σ1(g1,a2,g2,a2),σ2(g1,a2,g2,a2),p1(g1,a2,g2,a2)

(16)

式中:

(17a)

(17b)

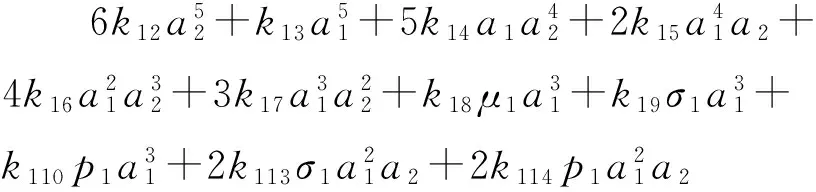
(17c)

(17d)

M2+M〈σ1,σ2,p1〉的生成元有18个:

(σ2a1,0), (p1a1,0), (σ1a2,0), (σ2a2,0),

(0,σ1a1), (0,σ2a1), (0,p1a1), (0,σ1a2),

(0,σ2a2), (0,p1a2)

(18)

下面证明,当(a1,a2,σ1,σ2,p1)=(0,0,0,0,0)时,(16)和(18)之间存在一个可逆矩阵A,使得两者可以互相表示:

(19)

式中:

(20a)

u2=(σ2(g1,a1,g2,a1)p1(g1,a1,g2,a1)a1(g1,a2,g2,a2)

a2(g1,a2,g2,a2)σ1(g1,a2,g2,a2)σ2(g1,a2,g2,a2)

(20b)

(σ2a1,0) (p1a1,0) (σ1a2,0) (σ2a2,0)

(20c)

(0,σ2a1) (0,p1a1) (0,σ1a2) (0,σ2a2)

(20d)

(20e)

(20g)

(20h)

式中:

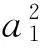
(21a)

(21b)

(21c)

(21d)

(21e)

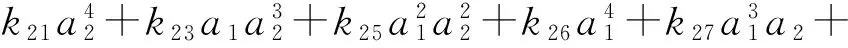
k28μ2a1a2+k29σ2a1a2+k210p1a1a2+

(21f)

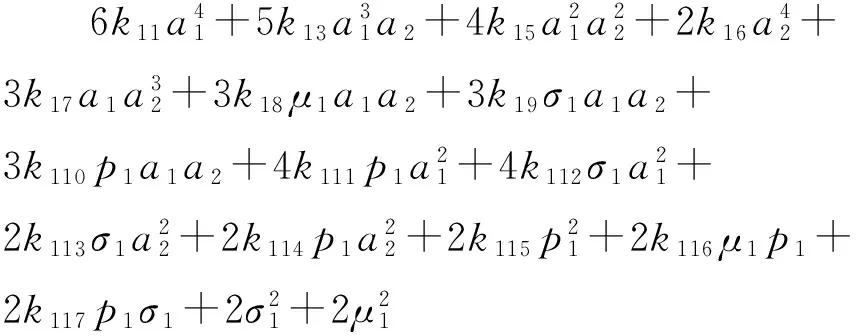
(21g)

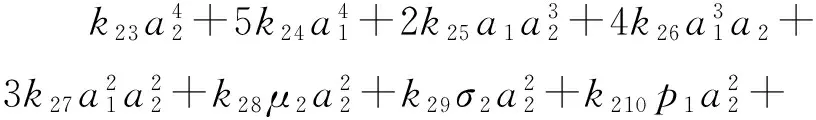
2k213σ2a1a2+2k214p1a1a2

(21h)

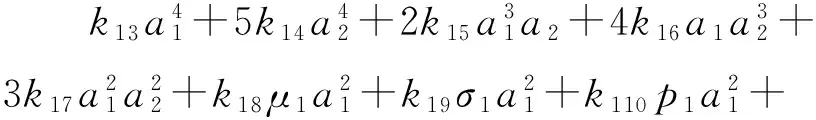
2k113σ1a1a2+2k114p1a1a2

(21i)

(21j)

因为μ1>0,μ2>0,当a1=a2=σ1=σ2=p1=0时,

(22)

这样矩阵A等于:

(23)

式中:

(24a)

(24b)

(24c)

(24d)

在14×18的矩阵A中,容易发现第1行和第5行线性相关,第4行和第11行线性相关,第7、8、9、13、14、15列是空的,剔除第5、11行和第7、8、9、13、14、15列,剩下一个12×12的矩阵,很容易证明12×12的矩阵的行列式的值是非零的.

证明完成.

1.3.2 简单识别

定理1.2令:

g(z,λ)=h(z,λ)+q(z,λ)

(25)

式中:

(26a)

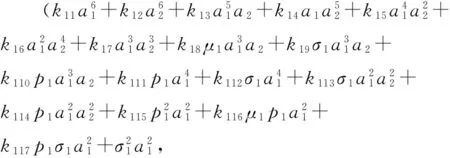
(26b)

可以得到g和h是强等价的.

证明:根据定理1.1,M2+M〈σ1,σ2,p1〉的一个高阶项是:

M3+M2〈σ1,σ2,p1〉

(27)

对于多项式g,我们观察发现:

(28a)

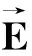
(28b)

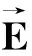
根据定理4.1(文献[10]中,第二册185页),可以得到g和h是强等价的.

证明完成.

在下面的讨论中,g将被h取代.

引理1.1h的非退化条件是:

(29)

满足非退化条件的h等价于:

(30)

证明:h是关于a1,a2的二次齐次多项式,根据方程(2.7) (文献[10]中,第一册402页),

(31)

根据方程(2.8)(文献[10]中,第一册402页),

(32)

因为μ1>0,μ2>0,

(33)

h的正规形式能够表示为:

(34)

证明完成.

观察表达式(34),h的普适开折需要表达式(34)补足h的线性项和常数项.

定理1.3令:

H(a1,a2,σ1,σ2,p1)=(h1(a1,a2,σ1,σ2,p1),h2(a1,a2,σ1,σ2,p1))是分叉问题h的一个4参数开折,如果满足引理1.1,则H是h的普适开折,当且仅当:

det(Q)=

(35)

式中γ是辅助参数,这里:

(a1,a2,σ1,σ2,p1,γ)=(0,0,0,0,0,0)

证明: 矩阵Q能够被表示为:

Q=(α1,α2,α3,α4,α5,α6)T

(36)

式中:

α1=(0,h1,a1a1,h1,a1a2,0,h2,a1a1,h2,a1a2)

(37a)

α2=(0,h1,a2a1,h1,a2a2,0,h2,a2a1,h2,a2a2)

(37b)

α3=(h1,σ1,h1,σ1a1,h1,σ1a2,h2,σ1,h2,σ1a1,h2,σ1a2)

(37c)

α4=(h1,σ2,h1,σ2a1,h1,σ2a2,h2,σ2,h2,σ2a1,h2,σ2a2)

(37d)

α5=(h1,p1,h1,p1a1,h1,p1a2,h2,p1,h2,p1a1,h2,p1a2)

(37e)

α6=(h1,γ,h1,γa1,h1,γa2,h2,γ,h2,γa1,h2,γa2)

(37f)

将h代入方程(37), 得到:

α1=(0,2,0,0,0,0),α2=(0,0,0,0,0,2),

α3=(0,0,0,0,0,0),α4=(0,0,0,0,0,0),

α5=(0,0,0,0,0,0),α6=(0,0,0,0,0,0)

(38)

在方程(38),仅有2个向量α1和α2是线性无关的,因此存在补足h的4个线性无关的向量:

(39)

式中λ,λ′和λ″的取值是σ1,σ2和p1三个分叉参数中的任意一个,且互相之间取值不同.

这样,我们得到:

(40)

把方程(40)代入方程(35),得到:

det(Q)≠0.

(41)

反过来,在方程(38)中,仅有向量α1和α2是线性无关,因为det(Q)≠0, 补足h的线性无关的向量需要4个:

(42)

这样,得到:

证明完成.

1.3.3 多项式空间的维数

定理1.4多项式空间能够简化为:

R{(dh)z,λ(Y1),…,(dh)z,λ(Ym),hλ,λhλ,λ2hλ,…}

=R{(a1,0),(0,a2)}

(43)

证明: 推导方程(43),建立下面的矩阵关系:

(44)

式中:

(45a)

(45b)

(45c)

(45d)

(45e)

(45f)

(45g)

(45h)

显然:

D1=2,D2=2

(46)

R{(dh)z,λ(Y1),…,(dh)z,λ(Ym),hλ,λhλ,λ2hλ,…}

=R{(a1,0),(0,a2)}

(47)

证明完成.

1.3.4 奇异性理论推广

根据定理1.1,有下面的关系:

h∈M2⊂M2+M〈σ1,σ2,p1〉

(48)

得到:

(49)

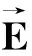
因此,对奇异性理论作如下的推广:

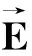
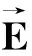
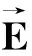
〈h〉⊕p(n)=T(h+1)

(50)

式中p(n)是一个有限维子空间.

同理,存在m个线性无关的向量补足T(h,1),使得

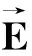
(51)

式中p′(m)是一个有限维子空间.

把方程(50)代入方程(51), 得到

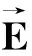
(52)

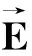
证明完成.

推论1.1n=6-2-m.

证明:根据定理1.3,存在6个线性无关的向量,但是在方程(38)中,仅有两个线性无关的向量α1和α2. 根据引理1.1, 可知2+m+n=6,即:n=6-2-m.

证明完成.

引理1.3让辅助参数γ∈R作用在单项式λl1xl2上, 如果l1≠0,则|γ|能够被剔除,sgn(γ)λl1xl2将被获得.

证明:对于γλl1xl2,如果l1≠0,|γ|能够嵌入在λl1中,得到sgn(γ)λl1,这是因为γ和λ都是参数,有共同的辅助特性.

证明完成.

在后面的讨论中,为了简化符号,sgn(γ)被记作ε.

1.3.5 普适开折

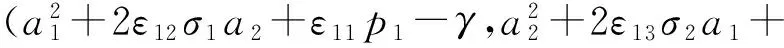
ε11p1+γ)

(53a)

ε21p1+γ)

(53b)

ε31σ1+γ)

(53c)

ε41σ1+γ)

(53d)

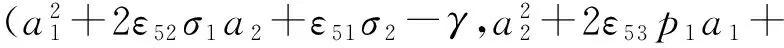
ε51σ2+γ)

(53e)

ε61σ2+γ)

(53f)

式中γ是辅助参数,εij=+1,0,-1；i=1,…,6；j=1,2,3.

证明:根据方程(2.7) (文献[10]中,第二册211页),可知:

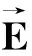
R{(a1,0),(0,a2)}

(54)

ItrT(h,1)是包含在T(h,1)中的极大理想:

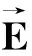
(55)

可知:

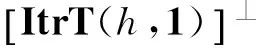
(σ2,0),(p1,0),(-1,0)

(0,a1),(0,a2),(0,σ1),

(0,σ2),(0,p1),(0,1)}

(56)

维数是12.

(a2,0), (0,a1), (σ1,0), (0,σ1), (σ2,0),

(0,σ2),(p1,0), (0,p1),(-1,0),(0,1)

(57)

根据定理1.3,简化方程(57),

(a2,0), (0,a1), (σ1,σ1), (σ2,σ2),

(p1,p1), (-1,1)

(58)

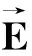
(σ1a1,0), (σ2a1,0), (p1a1,0), (σ1a2,0),

(σ2a2,0), (p1a2,0), (0,σ1a1), (0,σ2a1),

(0,p1a1), (0,σ1a2), (0,σ2a2), (0,p1a2)

(59)

在方程(58)中,对于向量(a2,0)和(0,a1),存在两个辅助参数β1和β2,使得(β1a2,0)和(0,β2a1)发生. 根据定理1. 3,(β1a2,0)和(σ1a2,0), (σ2a2,0), (p1a2,0)三个向量中的任意一个线性相关；(0,β2a1)和(0,σ1a1), (0,σ2a1), (0,p1a1)三个向量中的任意一个线性相关. 因此,(a2,0)和(0,a1)将被剔除.

在h的普适开折中,存在4个辅助参数α1,α2,α3和γ,使得(α1p1,α1p1),(α2σ1,α2σ1), (α3σ2,α3σ2)和(-γ,γ)发生,根据引理1.3,(ε1p1,ε1p1),(ε2σ1,ε2σ1),(ε3σ2,ε3σ2)和(-γ,γ)发生. 因为p1,σ1,σ2和γ都是参数,根据定理1.3,把四个向量(ε1p1,ε1p1),(ε2σ1,ε2σ1),(ε3σ2,ε3σ2)和(-γ,γ)代入方程(37)中,仅有两个向量是线性无关的,根据定义1.1,m=2.

根据定理1.3, 在矩阵Q中,可知向量(-γ,γ)必然发生.

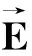
为了简化符号,(ε2σ1,ε2σ1)记作(ε1σ1,ε1σ1),(ε3σ2,ε3σ2)记作(ε1σ2,ε1σ2).

根据推论1.1,n=2.

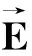
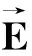
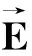
根据上面的分析,得到:

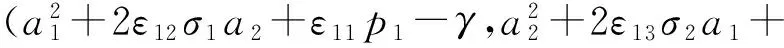
ε11p1+γ)

(60a)

ε21p1+γ)

(60b)

ε31σ1+γ)

(60c)

ε41σ1+γ)

(60d)

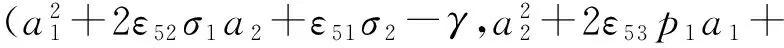
ε51σ2+γ)

(60e)

ε61σ2+γ)

(60f)

根据引理1.3,当所有隐辅助参数和辅助参数γ等于零,即:εij=0 (i=1,…,6;j=1,2,3)和γ=0,我们可以得到:

Gi(a1,a2,p1,0,0,0,0)=h(a1,a2,p1)

(61)

根据定理1.3,当εij≠0,对于方程(60)有:

(62a)

(62b)

(62c)

(62d)

(62e)

(62f)

证明完成.

1.3.6 转迁集

在下面的分析中,我们讨论方程(53)的转迁集.

对于方程(53a),分叉集满足的条件是:

(63a)

(63b)

(63c)

由方程(63c)的第三个等式,可得分叉集的表达式:

(64)

方程(63c)的第一和第二个等式,表明分叉发生时:

(a1,a2,σ1,σ2,p1,γ)=(0,0,0,0,0,0)

(65)

滞后集:

G=0, det(dG)=0和d2G(v,v)∈range(dG),

(66)

任意非零v∈ker(dG).

滞后集满足的条件:

(67a)

(67b)

a1a2-ε12ε13σ1σ2=0

(67c)

(67d)

式中v=(v1,v2).

我们假设σ1≠0和σ2≠0,则:

v=(a1,ε12σ1)

(68)

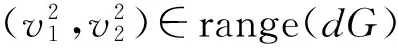
(69)

计算方程(69),可得:

(70)

让a1乘以方程(70)的两端,然后代入方程(67c)中,得到:

(71)

由方程(67c)和方程(71),可得:

(72)

方程(67a)加方程(67b),可得:

(73)

把方程(71)和方程(72)代入方程(73)中,得到滞后集的表达式:

(74)

双极限点集满足的条件:

(75a)

(75b)

a1a2-ε12ε13σ1σ2=0

(75c)

(a11,a21)≠(a12,a22),当p1=const

(75d)

根据方程(64)计算,可知:

σ1=0,p1≤0和σ2=0,p1≤0当ε11=1,

(76a)

σ1=0,p1≥0和σ2=0,p1≥0当ε11=-1

(76b)

我们定义ρ,θ和δ是fTσ2σ1-空间的圆柱坐标的转换,令:

σ1=ρ3cos3θ,σ2=ρ3sin3θ,p1=ρ6δ

(77)

把方程(77)代入方程(64)和方程(74)中,B,H和D有如下形式:

(78a)

(78b)

(78c)

同理,方程(53b),(53c), (53d),(53e)和(53f)的转迁集∑也能够被获得.

2 数值模拟

本节利用Runge-Kutta法对方程(53a)进行数值计算,针对分叉表达式,滞后表达式和双极限点集得到关于三个分叉参数σ1,σ2和p1的平面转迁集和立体转迁集,同时给出了相应的力-幅图.

根据以上分析结果,对方程(53a)进行数值计算,由方程(64)和方程(74),我们得到方程(53a)关于三个分叉参数σ1,σ2和p1的平面转迁集和立体转迁集,当ε11=-1时,如图1和图2所示；当ε11=1时,如图5和图6所示,B表示分叉集,H表示滞后集,D表示双极限点集. 从方程(64)的表达式可以发现,当p1固定时,在图2(a)中,分叉集是一个圆；当σ1或σ2固定时,在图2(a)中,分叉集是一个抛物线.

图1和图2将方程(53a)平衡点附近邻域分为不同的区域,分别对应点阵夹芯板不同的振动形式,在区域(1)中方程(53a)有一个零解；在区域(2)中方程(53a)有两个零解；在区域(3)中方程(53a)没有零解.

图1 ε11=-1时方程(53a)的平面转迁集Fig. 1 Plan transition variety for Equation (53a) when ε11=-1

图2 ε11=-1时方程(53a)的三维转迁集Fig.2 Three-dimensional sketch of Transitions variety for Equation (53a) when ε11=-1

图3表示,当ε11=-1,ε12=1和ε13=1时,方程(53a)的第一阶模态的力-幅响应,其对应参数值分别为:

(a)σ1=-3,σ2=-1,γ=0

(b)σ1=-1,σ2=-3,γ=0

(c)σ1=-3,σ2=-1,γ=1

(d)σ1=-1,σ2=-3,γ=1

图4表示,当ε11=-1,ε12=1和ε13=1时,方程(53a)的第二阶模态的力-幅响应,其对应参数值分别为:

(a)σ1=-1,σ2=-3,γ=0

(b)σ1=-3,σ2=-1,γ=0

(c)σ1=-1,σ2=-3,γ=1

(d)σ1=-3,σ2=-1,γ=1

图3 ε11=-1时方程(53a)在不同参数下第一阶模态的力-幅响应曲线Fig.3 Force-amplitude response curves of the first-order mode with different parameters for Equation (53a) when ε11=-1

图4 ε11=-1时方程(53a)在不同参数下第一阶模态的力-幅响应曲线Fig.4 Force-amplitude response curves of the second-order mode with different parameters for Equation (53a) when ε11=-1

同理,图5和图6将方程(53a)平衡点附近邻域分为不同的区域,分别对应点阵夹芯板不同的振动形式,在区域(1)中方程(53a)有一个零解；在区域(2)中方程(53a)有两个零解；在区域(3)中方程(53a)没有零解.

图7表示,当ε11=1,ε12=1和ε13=1方程(53a)的第一阶模态的力-幅响应,其对应参数值分别为:

(a)σ1=-3,σ2=-1,γ=0

(b)σ1=-1,σ2=-3,γ=0

(c)σ1=-3,σ2=-1,γ=1

(d)σ1=-1,σ2=-3,γ=1

图5 ε11=1时方程(53a)的平面转迁集Fig.5 Plan transition variety for Equation (53a) when ε11=1

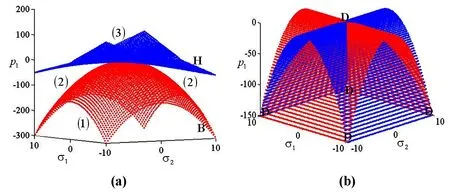
图6 ε11=1时方程(53a)的三维转迁集Fig.6 Three-dimensional sketch of Transitions variety for Equation (53a) when ε11=1

图7 ε11=1时方程(53a)在不同参数下第一阶模态的力-幅响应曲线Fig.7 Force-amplitude response curves of the first-order mode with different parameters for Equation (53a) when ε11=1

图8表示,当ε11=1,ε12=1和ε13=1时,方程(53a)的第二阶模态的力-幅响应,其对应参数值分别为:

(a)σ1=-1,σ2=-3,γ=0

(b)σ1=-3,σ2=-1,γ=0

(c)σ1=-1,σ2=-3,γ=1

(d)σ1=-3,σ2=-1,γ=1

图8 ε11=1时方程(53a)在不同参数下第二阶模态的力-幅响应曲线Fig.8 Force-amplitude response curves of the second-order mode with different parameters for Equation (53a) when ε11=1

同样的方法,也可以对方程(53b)、(53c)、 (53d)、 (53e)和(53f)进行数值计算,针对分叉表达式,滞后表达式和双极限点集得到关于三个分叉参数σ1、σ2和p1的平面转迁集和立体转迁集.

3 结论

针对1:1内共振情况下点阵夹芯板的非线性动力学分叉方程,推广了对于含有两个状态变量和三个及三个以上分叉参数的一般非线性动力学方程的奇异性理论,得到点阵夹芯板的非线性力学分叉方程余维4的6个普适开折的表达式,从方程(64)的表达式可以发现:当p1固定时,分叉集是一个圆；当σ1或σ2固定时,分叉集是一个抛物线,同时,在区域(1)中,方程(53)有一个零解；在区域(2)中方程(53)有两个零解；在区域(3)中方程(53)没有零解. 研究结果对理解点阵夹芯板结构的稳定性具有指导意义,并为该类构件的工程应用提供参考.

1Queheillalt D T, Murty Y,Wadley H N G. Mechanical properties of an extruded pyramidal lattice truss sandwich structure.ScriptaMaterialia, 2008,58(1):76～79

2Lim C H, Jeon I, Kang K J. A new type of sandwich panel with periodic cellular metal cores and its mechanical performances.MaterialsandDesign, 2009,30(8):3082～3039

3Park J S, Joo J H, Lee B C,et al. Mechanical behaviour of tube-woven Kagome truss cores under compression.InternationalJournalofMechanicalSciences, 2011,53(1):65～73

4Kim T,Hodson H P,Lu T J. Fluid-flow and end wall heat-transfer characteristics of an ultralight lattice-frame materia1.InternationalJournalofHeatandMassTransfer, 2004,47(6-7):1129～1140

5Kim T,Hodson H P,Lu T J. Contribution of vortex structures and flows eparation to local and overall pressure and heat transfer characteristics in an ultralight weight lattice material.InternationalJournalofHeatandMassTransfer, 2005,48(19-20):4243～4264

6Lu T J,Valdevit L,Evans A G. Active cooling by metallic sandwich structures with periodic cores.ProgressinMaterialsScience, 2005,50(7):789～815

7Golubitsky M, Langford W F. Classification and unfoldings of degenerate Hopf bifurcations.JournalofDifferentialEquations, 1981,41(3):375～415

8Golubitsky M, Guillemin V. Stable mapping and their singularities. New York:Graduate Texts in Mathematics, 1973

9Martinet J. Singularities of smooth functions and maps. Landon:Cambridge University Press, 1982

10 Golubistky M S, Schaeffer D G. Singularities and groups in bifurcation theory. New York :Spring-Verlag, 1988,220(4):1023～1074

11 Keyfitz B L. Classification of one state variable bifurcation problem up to codimension seven.DynamicsandStabilityofSystems, 1986,1(1):1～41

12 Golubitsky M,Stewart I. Hopf bifurcation with dihedral group symmetry: coupled nonlinear oscillators.MultiparameterBifurcationTheory, 1986:131～173

13 Melbourne I. The classification up to low codimension of bifurcation problems with octahedral symmetry[Ph.D Thesis]. Coventr:University of Warwick, 1988

14 Gaffney T. New methods in the classification theory of bifurcation problem.MultiparameterBifurcationTheory, 1986,56:97～116

15 Furter J E,Sitta A M,Stewart I. Singularity theory and equivariant bifurcation problems with parameter symmetry.MathematicalProcEedingsoftheCambridgePhiloSophicalSocietyR.M.Loynes, 1996,120(3):547～578

16 Gao S P, Li Y C. Classification of (D4,S1)-equivariant bifurcation problems up to topological condition 2.ScienceinChina.Ser, 2003,46(6):862～871

17 郭瑞芝. 等变分歧问题研究[博士学位论文]. 长沙:中南大学,2006 (Guo R Z. Study on equivariant bifurcation problems[Ph.D Thesis]. Changsha: Central South University, 2006 (in Chinese))

18 崔登兰,李养成. 含两组状态变量且参数具有对称性的等变分歧问题及其开折的稳定性. 应用数学和力学, 2007,28(2):209～215 (Cui D L, Li Y C. Equivariant bifurcation problems and the stability of open fold under contains two sets of state variables and parameters which have symmetry.AppliedMathematicsandMechanics, 2007,28(2):209～215 (in Chinese))

19 Lari-Lavassani A H, Lu Y C. Equivariant multiparameter bifurcation via singularity theory.JournalofDynamicsandDifferentialEquations, 1993,5(2):189～218

20 胡凡努,李养成. 关于两状态变量组的等变分歧问题的通用开折. 数学理论与应用, 2000,20(3):50～57 (Hu F N, Li Y C. Versal unfolding of equivariant bifurcation problems about two sets of state variables.MathematicalTheoryandApplications, 2000,20(3):50～57 (in Chinese))

21 高守平,李养成. 多参数等变分歧问题关于左右等价的开折. 数学年刊A辑, 2003,24(3):341～348 (Gao S P, Li Y C. Open fold of equivariant bifurcation problems with multiparameter under the left and right equivalent group.ChineseAnnalsofMathematics,SeriesA, 2003,24(3):341～348 (in Chinese))

22 郭瑞芝,李养成. 含两组状态变量的等变分歧问题在左右等价群下的开折. 应用数学和力学, 2005,26(4):489～496 (Guo R Z, Li Y C. Open fold of equivariant bifurcation problems with two sets of state variables under the left and right equivalent group.AppliedMathematicsandMechanics, 2005,26(4):489～496 (in Chinese))

23 Qin Z H, Chen Y S. Singular analysis of bifurcation systems with two parameters.ActaMechanicaSinica, 2010,26(3):501～507

24 Qin Z H, Chen Y S. Singular analysis of a two-dimensional bifurcation system.ScienceChinaTechnologicalSciences, 2010,53(3):608～611

25 Qin Z H,Chen Y S, Li J. Singular analysis of two-dimensional elastic cable with 1:1 internal resonance.AppliedMathematicsandMechanics, 2010,31(2):143～150

26 秦朝红. 两状态变量、两分叉参数系统的分叉分析及其工程应用[博士学位论文]. 哈尔滨:哈尔滨工业大学, 2010 (Qin Z H. Singularity method for nonlinear dynamical analysis of systems with two parameters and its application in engineering[Ph.D Thesis]. Harbin: Harbin Institute of Technology, 2010(in Chinese))

27 陈建恩. 轻质材料层合板的非线性动力学理论分析与实验研究[博士学位论文]. 北京:北京工业大学,2013 (Chen J E. Theoretical and experimental investigations on nonlinear dynamics of light-weight sandwich plate[Ph.D Thesis]. Beijing: Beijing University of Technology, 2013(in Chinese))