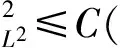
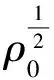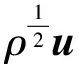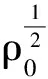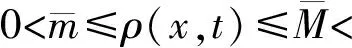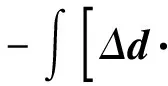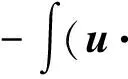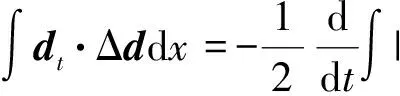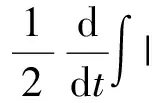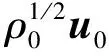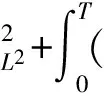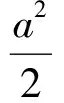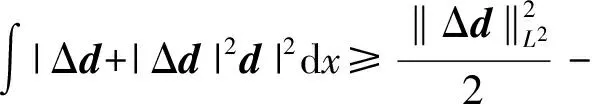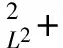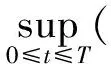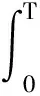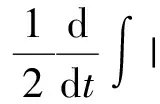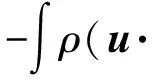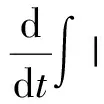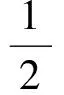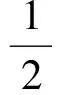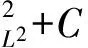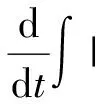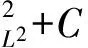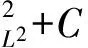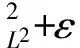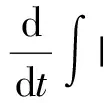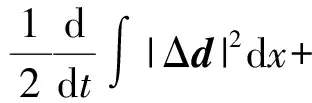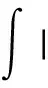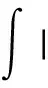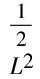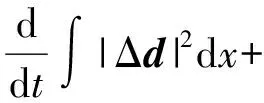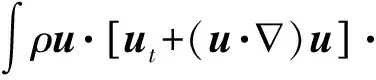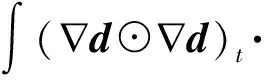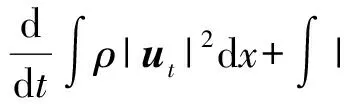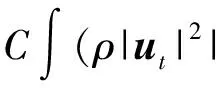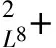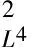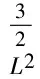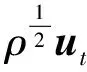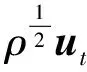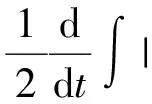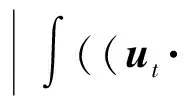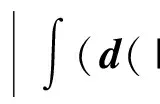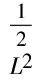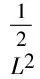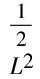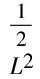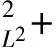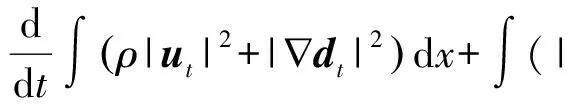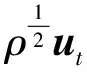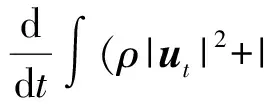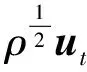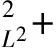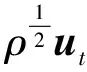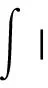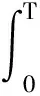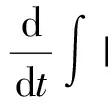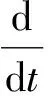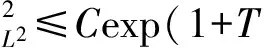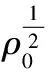二维不可压缩 Navier-Stokes-Landau-Lifshitz方程组的整体强解

2018-01-11黄丙远黄金锐

华南师范大学学报（自然科学版） 2017年6期

关键词：分部方程组向量

黄丙远 , 黄金锐 , 奚悦

(1. 韩山师范学院数学与统计学院，潮州 521041； 2. 五邑大学数学与计算科学学院，江门 529020)

二维不可压缩 Navier-Stokes-Landau-Lifshitz方程组的整体强解

黄丙远1*, 黄金锐2, 奚悦2

(1. 韩山师范学院数学与统计学院，潮州 521041； 2. 五邑大学数学与计算科学学院，江门 529020)

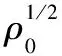
Navier-Stokes-Landau-Lifshitz 方程组; Cauchy 问题; 整体存在性

本文考虑不可压缩 Navier-Stokes-Landau-Lifshitz 耦合模型[1-2]，研究其在2×(0,)中对应的Cauchy问题,具体如下:

ρt+·(ρu)=0,

(1)

ρut+ρu·u+P=Δu-·(d⊙d),

(2)

·u=0,

(3)

dt+(u·)d=Δd+|d|2d+d×Δd,|d|=1,

(4)

(ρ,u,d)(x,0)=(ρ0,u0,d0),·u0=0,|d0|=1,x2,

(5)

(ρ,u,d)(x,t)→(0,0,1),|x|→,t>0,

(6)

其中(ρ,u,P,d)分别表示密度函数、速度函数、压力项及磁矩,u=(u1,u2),“1”为单位向量. 在动量守恒方程中出现的d⊙d表示以id·jd作为第(i,j)元的2×2矩阵,1≤i,j≤2. 当d为常值单位向量时,方程组(1)～(3)是Navier-Stokes方程组[3-4]. 若方程(4)的u=0,则方程(4)为Landau-Lifshitz方程[5]. 若方程(4)中忽略d×Δd,则方程(1)～(4)就是液晶系统,其研究成果可见文献[6-9].

受到文献[6]、[8]的启发,本文将研究耦合方程组(1)～(6)的强解,得到整体强解的存在唯一性.

1 预备知识

为了方便起见,全文作了一些记号：

Hk=Wk,2,Dk,r=Dk,r(2)={v(2):‖kv‖Lr<},

Wk,r=Lr∩Dk,r,Dk=Dk,2,D1={vL6:‖v‖L2<}.

强解的定义如下：

定义1假设T>0, 如果(ρ,u,P,d)在2×(0,T)中几乎处处意义下满足方程组(1)～(6),且

ρL((0,T);2),ρ,ρtL(0,T;L2),

uL(0,T;H2),uL2(0,T;W1,4),

utL(0,T;L2)∩L2(0,T;H1),

PL(0,T;H1)∩L2(0,T;W1,4),

dL(0,T;H2)∩L2(0,T;H3),

dtL(0,T;H1)∩L2(0,T;H2),dttL2(0,T;L2),

则称(ρ,u,P,d)是方程组(1)～(6)在2×(0,T)中的强解.

引理1假设初值(ρ0，u0,d0)满足0

证明利用文献[6]的迭代方法或者文献[10]的Galerkin方法及文献[3]、[10]中标准的区域扩张技术,都能得到问题(1)～(6)的局部强解的存在唯一性.

引理2[11]对于任意p[2,)、q(1,)及r(2,),假设fH1和gLq∩D1,r,那么存在仅仅依赖于p、q和r的正常数C,满足

与

‖g‖C(2)≤C‖g‖‖g‖.

2 主要结论

定理1假设0

那么对于任意给定的0

在引理1已经得到唯一局部强解的前提下, 为了证明定理1, 本文只需要建立一系列关于时间T全局性的先验估计. 为方便起见，全文出现的正常数C与C0仅依赖于初值(ρ0,u0,d0),而不依赖于ρ、u、d及时间T. 下面,对于任意的T>0,将建立一些有用的先验估计.

引理3(基本能量等式)对于所有的t[0,T],有

(7)

而且

(8)

证明用u与方程(2)做向量积,然后在2上积分,并利用分部积分法与方程(3),得

(9)

用(Δd+|d|2d)与方程(4)做向量积,然后在2上积分,由于(Δd+|d|2d)·(d×Δd)=0,得

(10)

由|d|=1推出

(dt+u·d)·|d|2d=[|d|2(|d|2)t+

u·(|d|2)|d|2]=0,

(11)

及方程(6)推出

(12)

所以,联立式(10)～(12),得到

(13)

把式(9)和式(13)相加,并在[0,T]上积分,式(7)显然成立.

最后,利用特征线方法[12]可得式(8).

(14)

证明由式(7)与式(8)可直接得到

(15)

(16)

把式(16)代入式(13),应用引理2、引理3、Cauchy不等式、式(9)及式(15),则

‖u‖L4‖d‖L4‖Δd‖L2≤C0‖d‖‖Δd‖

C0‖d‖‖Δd‖‖Δd‖‖u‖

(17)

(18)

(19)

对方程(4)应用L2估计,借助Hölder不等式、引理2、式(7)及式(15),得

(20)

联立式(7)与式(19),得

(21)

由式(15)、(19)、(21)直接得到式(14).

引理4对于任意T≥0, 有

(22)

证明用ut与方程(2)做向量积,在2上积分,利用分部积分关系、方程(3)及式(8),得

由式(8)、Hölder不等式、Cauchy不等式及引理2,得

C(‖u‖L4‖u‖L4‖ut‖L2+‖Δd‖L4‖d‖L4‖ut‖L2)≤

(23)

根据Cauchy不等式,式(23)变为

Cε(‖Δd‖

(24)

根据定常Stokes方程的正则性理论[13],由方程(2)、Hölder不等式、引理2及Cauchy不等式,得

利用Cauchy不等式,则

(25)

把式(25)代入式(24),有

Cε(‖u‖‖Δd‖‖Δd‖).

(26)

对方程(4)作用算子Δ,并用Δd与之做向量积,在2上积分,利用分部积分法和Hölder不等式,得

(27)

接着,估计I1、I2. 由引理2、引理3、推论1及Cauchy不等式,有

I1≤C(‖d‖L2‖Δd‖L2+‖d‖‖Δd‖L2‖Δd‖+

‖Δd‖L2‖Δd‖+‖Δd‖)‖Δd‖L2≤

ε‖Δd‖

(28)

ε‖Δd‖‖u‖‖Δd‖‖u‖).

(29)

把式(28)、(29)代入式(27),取ε足够小,得

C(‖u‖‖Δd‖‖Δd‖‖u‖).

(30)

由式(26)、(30),得

C(‖u‖‖Δd‖

(31)

由Gronwall不等式、引理3和推论1,得

(32)

由方程(20)及式(32),得

(33)

由推论1及式(22)、(25)、(32)、(33)，得

(34)

则由估计式(32)～(34)可得式(22).

引理5对于任意T≥0,有

对方程(2)关于时间t求导,则

ρutt+ρ(u·)ut-Δut+Pt=-ρt[ut+(u·)u]-

ρut·u-(·(d⊙d))t.

(35)

用ut与方程(35)做向量积,在2上积分,利用方程(1)、(3),并由分部积分法,得

根据Cauchy不等式、Hölder不等式、引理2～引理4和推论1,得

ρ|u||u|2|ut|+ρ|u|2|2u||ut|+ρ|u|4|u|2)dx+

(36)

对方程(4)关于t求导,则

dtt+(ut·)d+(u·)dt-Δdt=

(37)

用Δdt与方程(37)做向量积,在2上积分,得

(38)

由Hölder不等式、引理 2～引理4、推论1及Cauchy不等式,对J1、J2、J3估计如下：

J1≤C(‖ut‖L4‖d‖L4‖Δdt‖L2+‖u‖L4‖dt‖L4‖Δdt‖L2)≤

ε(‖ut‖‖Δdt‖‖ut‖‖dt‖

J2+J3≤C(‖d‖L4‖dt‖L4‖Δdt‖L2+

‖dt‖L4‖d‖‖Δdt‖L2)+C(‖dt‖L4‖Δd‖L4‖Δdt‖L2)≤

C(‖dt‖‖dt‖‖Δdt‖L2+‖dt‖‖Δdt‖)+

把上述估计代入式(38),然后与式(36)相加,得

ε(‖ut‖‖Δdt‖+Cε(‖ut‖‖2u‖

(39)

取ε足够小,式(39)变为

(40)

由Gronwall不等式、引理3、引理4及推论1,有

(41)

联立式(8)及式(41),得

(42)

对方程(4)关于x求导,则

(43)

(44)

由Hölder不等式、Cauchy不等式、引理2～引理4,有以下估计：

K1≤C‖dt‖L2‖Δd‖L2≤ε‖Δd‖‖dt‖

K2≤C‖u‖L2‖d‖L‖Δd‖L2≤ε‖Δd‖

K3+K4≤C(‖u‖L4+‖d‖L4)‖2d‖L4‖Δd‖L2≤

ε‖Δd‖‖Δd‖‖Δd‖

K5+K6≤C‖d‖L4‖Δd‖L4‖Δd‖L2≤

ε‖Δd‖Cε‖Δd‖‖Δd‖

把上述估计代入式(44),取ε足够小,根据估计式(41),有

‖Δd‖‖dt‖C.

(45)

类似地，也能相应地得到

(46)

联立式(41)、(42)与式(45)、(46),引理5得证.

引理6对任意T>0，有

(47)

与

(48)

证明由式(25)、(42)、(14)、(45),立即得到

‖u‖‖P‖C.

(49)

根据定常Stokes方程的正则性理论[3,13]、Hölder不等式及引理2,得

C(‖ρut‖L4+‖ρu·u‖L4+‖·(d⊙d)‖L4)≤

C(‖ρ‖L‖ut‖L4+‖ρ‖L‖u‖L‖u‖L4+

‖Δd‖L2‖Δd‖L2+‖Δd‖H1)≤

C(‖ut‖H1+‖u‖H1+‖Δd‖H1).

(50)

在t[0,T]上,式(50)关于t积分, 由式(7)、(14)、(22)及引理5，得

(51)

结合式(49)、(51)可证得式(47)成立.

(ρ)t+u·2ρ+u·ρ=0.

(52)

(53)

根据引理2,得

‖u‖L≤C‖u‖‖2u‖.

(54)

把式(54)代入式(53),应用引理4,得

(55)

对式(55)应用Gronwall不等式,结合式(51),得

‖ρ‖).

定理1的证明结合引理3～引理6及引理1中得到的局部强解,充分地证明了：对于任意给定的时间T(0

[1] FAN J S,GAO H J,GUO B L. Regularity criteria for the Navier-Stokes-Landau-Lifshitz system[J]. Journal of Mathematical Analysis and Applications,2010,363(1):29-37.

[2] ZHAI X P,LI Y S,YAN W. Global solutions to the Navier-Stokes-Landau-Lifshitz system[J]. Mathematische Nachrichten,2016,289(3):377-388.

[3] JUN C H,KIM H. Strong solutions of the Navier-Stokes equations for nonhomogeneous incompressible fluids[J]. Communications in Partial Differential Equations,2003,28(5):1183-1201.

[4] KIM H. A blow up criterion for the nonhomogeneous incompressible Navier-Stokes equations[J]. SIAM Journal on Mathematical Analysis,2006,37(5):1417-1434.

[5] GUO B L,DING S J. Landau-Lifschitz equations[M]. Singapore:World Scientific,2008.

[6] WEN H Y,DING S J. Solutions of incompressible hydrodynamic flow of liquid crystals[J]. Nonlinear Analysis:Real World Applications,2011,12(3):1510-1531.

[7] LIN F H,LIN J Y,WANG C Y. Liquid crystal flows in two dimensions[J]. Archive for Rational Mechanics & Analysis,2010,197(1):297-336.

[8] DING S J,HUANG J R,XIA F G. Global existence of strong solutions for incompressible hydrodynamic flow of liquid crystals with vacuum[J]. Filomat,2013,27(7):1247-1257.

[9] 丁时进. 液晶模型的分析理论[J]. 华南师范大学学报(自然科学版),2013(3):1-7.

DING S J. Mathematical analysis for the models of liquid crystals[J]. Journal of South China Normal University(Natural Science Edition),2013(3):1-7.

[10] HUANG T,WANG C Y,WEN H Y. Strong solutions of the compressible nematic liquid crystal flow[J]. Journal of Differential Equations,2012,252(3):2222-2265.

[11] NIRENBERG L. On elliptic partial differential equations[J]. Annali della Scuola Normale Superiore di Pisa-Classe di Scienze,1959,13(2):115-162.

[12] LADYZHENSKAYA O A,SOLONNIKOV V A. Unique solvability of an initial and boundary value problem for viscous incompressible nonhomogeneous fluids[J]. Journal of Soviet Mathematics,1978,9(5):697-749.

[13] GALDI G P. An introduction to the mathematical theory of the Navier-Stokes equations[M]. New York:Springer,1994.

Global Strong Solutions for 2D Incompressible Navier-Stokes-Landau-Lifshitz Equations

HUANG Bingyuan1*, HUANG Jinrui2, XI Yue2

(1. School of Mathematics and Statistics, Hanshan Normal University, Chaozhou 521041, China; 2. School of Mathematics and Computational Science,Wuyi University, Jiangmen 529020, China)