姚晓洁， 秦发金

(广西科技师范学院数学与计算机科学学院，来宾 546199)

具有收获率的扩散捕食系统的8个正概周期解

姚晓洁*， 秦发金

(广西科技师范学院数学与计算机科学学院，来宾 546199)

提出了一类具有收获率和Hassell-Varley功能反应的扩散捕食系统，通过利用重合度理论中的延拓定理和不等式分析技巧,细致分析了该系统解的先验界的8种可能存在情形，从而获得了其至少存在8个正概周期解的充分条件.

收获率; Hassell-Varley功能反应;扩散捕食系统; 8个正概周期解; 重合度

近年来，关于具有时滞的生物种群系统具有多个周期解的研究引起了学者们的广泛兴趣，并取得一些有意义的结果[1-6]. 众所周知，自然界中生物种群很多不是周期现象，而是概周期现象，因此，研究生物种群系统的概周期解更具现实意义. 最近，ZHANG和WEI[7]讨论了如下具有收获率和Hassell-Varley功能反应的捕食系统

(1)

的概周期解问题，利用重合度理论获得了系统(1)至少存在2个正概周期解的充分条件. 除了时滞的影响外，扩散现象也经常在生物种群系统中发生[8-12]. 然而，对扩散的生物种群系统具有多个正概周期解却很少有人研究. 因此，本文在文献[7]的基础上讨论如下具有收获率和Hassell-Varley功能反应的时滞扩散捕食系统

(2)

的概周期解的存在性,其中Ni(t)(i=1,2)分别表示种群A在斑块1和斑块2中的种群密度,N3(t)表示种群B在斑块1的种群密度；种群A可在斑块1和斑块2中扩散,Dj(j=1,2)为扩散系数,hi>0 (i=1,2,3)为收获率;ai(t)、bi(t)、hi(t)、Dj(t)、cj(t)、(t) (i=1,2,3；j=1,2)均为非负的连续概周期函数；γ(0,1),θi(i=1,2,3)为正常数.

1 准备知识

定义1称函数x(t)C()=C(,)在是概周期解，如果对∀ε>0，集合

T(x,ε)={:|x(t+)-x(t)|<ε,∀t}

是相对稠密的，即对∀ε>0，存在一个实数l=l(ε)，使得在每个长度为l的区间内至少有一个=(ε)T(x,ε)，使得|x(t+)-x(t)|<ε(∀t)成立. 集合T(x,ε)叫做x(t)的ε-概周期集,叫做x(t)的ε-概周期，l(ε)为T(x,ε)的包含区间长度.

记

AP()={p(t):p(t)是上实值概周期函数}，

AP(,n)={(x1,x2,…,xn)T:xiAP(),i=1,2,…,n,n+}.

引理1[13]如果f(t)AP()，则f(t)在有界.

引理2[14]如果f(t)AP()，则存在t0使得f(t0)=m(f).

引理3[7]假设x(t)AP()∩C1()且x′(t)C()，记则对∀ε>0，下列结论成立：

(i)存在点ξε[0,+)，使得x(ξε)[x*-ε,x*]和x′(ξε)=0.

(ii)存在点ηε[0,+)，使得x(ηε)[x*,x*+ε]和x′(ηε)=0.

设X和Z是Banach空间，L:DomL⊂X→Z为线性映射，N:X×[0,1]→Z为连续映射，若dim KerL=codim ImL<+，且ImL在Z中是闭的，则称映射L是零指标的Fredholm映射. 如果L是零指标的Fredholm映射，且存在连续投影P:X→X及Q:Z→Z使得ImP=KerL，ImL=KerQ=Im(I-Q)，及X=KerL⊕KerP,Z=ImL⊕ImQ，则L|Dom L∩Ker P:(I-P)X→ImL可逆，并设其逆映射为KP. 设Ω为X中有界开集，若有界且KP(I-Q)N:×[0,1]→X是紧的，则称N在×[0,1]上是L-紧的. 由于ImQ与KerL同构，因而存在同构映射J:ImQ→KerL.

(ii)QN(x,0)≠0,∀x∂Ω∩KerL;

(iii) deg{JQN(x,0),Ω∩KerL}≠0,

作变换Ni(t)=eui(t)(i=1,2,3)，则系统(2)变为

(3)

对xAP()，定义

V1={z=(u1,u2,u3)TAP(,3),mod(u1)⊂mod(Lu1),

mod(u2)⊂mod(Lu2),mod(u3)⊂mod(Lu3),

∀μΛ(u1)∪Λ(u2)∪Λ(u3),|μ|≥α},

V2={z(t)≡(c1,c2,c3)T3},

其中

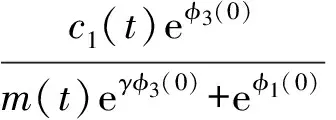
且φiC([-σ,0],是给定的正常数. 定义范数

类似文献[5]的证明，容易得到：

引理5范数定义中的X和Z是Banach空间.

引理7定义N:X×[0,1]→Z,N(z(t),)=(N1(z(t),),N2(z(t),),N3(z(t),))T,这里

N1(z(t),)=a1(t)-b1(t)eθ1u1(t)-

N2(z(t),)=a2(t)-b2(t)eθ2u2(t)+

N3(z(t),)=a3(t)-b3(t)eθ3u3(t)+

及

P:X→X,Px=m(x);Q:Z→Z,Qz=m(z),

为了得到本文结果，考虑下面辅助方程

h(x-)=h(x+)=0；h(x)>0,x(x-,x+);

h(x)<0,x(0,x-)∪(x+,+);h′(x-)>0,h′(x+)<0.

作如下假设：

再记

由引理8，类似文献[5]中引理3.3的证明,易得:

引理9假设(A1)满足，则下列结论成立:

2 主要结果

定理1假设条件(A1)、(A2)满足，则系统(2)至少存在8个不同的正概周期解.

证明为了应用引理4来证明系统(2)至少存在8个正概周期解，只需在X中找到8个有界开集即可. 考虑方程Lz=N(z,),(0,1)，即

(4)

假设(u1(t),u2(t),u3(t))TDomL⊂X是方程(4)对某个(0,1)的概周期解，其中DomL={(u1,u2,u3)TX:u1,u2,u3C1(),,,C()}. 则由引理3可知，对任意ε(0,1)，存在ξi=ξi(ε),ηi=ηi(ε)[0,+) (i=1,2,3)，使得

(5)

这里

结合方程(4)有

(6)

a2(ξ2)-b2(ξ2)eθ2u2(ξ2)+D2(ξ2)-=0,

(7)

a3(ξ3)-b3(ξ3)eθ3u3(ξ3)+

(8)

(9)

a2(η2)-b2(η2)eθ2u2(η2)+

(10)

a3(η3)-b3(η3)eθ3u3(η3)+

(11)

由式(5)、(6)可得

(12)

类似地，由式(5)、(7)可得

(13)

下面分2种情形讨论.

(14)

(15)

由式(14)、(15)可得

(16)

由式(5)、(8)可得

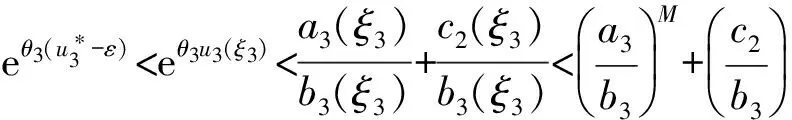
并令ε→ 0，有

(17)

由式(6)、(17)可得

综上所述，必有

u1(t)(ln,ln)∪(ln,max{ln,lnN1}),

u2(t)(ln,ln)∪(ln,max{ln,lnN1}),

u3(t)(ln,ln)∪(ln,max{ln,lnN2}).

Ω1={u=(u1,u2,u3)TX|u1(ln,max{ln,lnN1}),

u2

u3(ln,max{ln,lnN2})},

Ω2={u=(u1,u2,u3)TX|u1(ln,max{ln,lnN1}),

u2

u3(ln,max{ln,lnN2})},

Ω3={u=(u1,u2,u3)T

u2

u3(ln,max{ln,lnN2})},

Ω4={u=(u1,u2,u3)T

u2

u3(ln,max{ln,lnN2})},

Ω5={u=(u1,u2,u3)TX|u1(ln,max{ln,lnN1}),

u2

u3

Ω6={u=(u1,u2,u3)TX|u1(ln,max{ln,lnN1}),

u2(ln,ln),u3(ln,ln)},

Ω7={u=(u1,u2,u3)T

u2

u3

Ω8={u=(u1,u2,u3)T

u2(ln,ln),u3(ln,ln)}.

显然,Ωi(i=1,2,…,8)是X上的开集,且Ωi∩Ωj=∅(i,j=1,2,…,8,i≠j),从而Ωi(i=1,2,…,8)满足引理1的条件(i).

现在证明引理4的条件(ii)也成立，即证若u∂Ωi∩KerL=∂Ωi∩3时有QN(u,0)≠0(i=1,2,…,8). 假设QN(u,0)=0,由引理2知，存在t0使得

(18)

由引理9(ii)容易得到式(18)有8个不同的解：

由于KerL=ImQ,取J=I,根据引理9 (ii)直接计算可得

deg{JQN(u,0),Ω1∩KerL,0}=-1,

deg{JQN(u,0),Ω2∩KerL,0}=1,

deg{JQN(u,0),Ω3∩KerL,0}=1,

deg{JQN(u,0),Ω4∩KerL,0}=-1,

deg{JQN(u,0),Ω5∩KerL,0}=1,

deg{JQN(u,0),Ω6∩KerL,0}=-1,

deg{JQN(u,0),Ω7∩KerL,0}=-1,

deg{JQN(u,0),Ω8∩KerL,0}=1.

这说明引理4的条件(iii)成立. 故根据引理4知，系统(2)至少存在8个不同的概周期解.

由定理1和引理10立即可得：

推论1如果条件(A2)成立，且下面条件满足：

则系统(2)至少存在8个不同的正概周期解.

[1] WEI F Y. Existence of multiple positive periodic solutions to a periodic-prey system with harvesting terms and Holling Ⅲ type functional response[J]. Communications in Nonlinear Science and Numerical Simulation,2011,16(4):2130-2138.

[2] ZHANG Z Q,HOU Z T. Existence of four positive periodic solutions for a ratio-dependent predator-prey system with multiple exploited (or harvesting) terms[J]. Nonlinear Analysis Real World Applications,2010,11(3):1560-1571.

[3] HU D W,ZHANG Z Q. Four positive periodic solutions to a Lotka-Volterra cooperative system with harvesting terms[J]. Nonlinear Analysis:Real World Applications,2010,11(2):1115-1121.

[4] FAN Y H,WANG L L. Multiplicity of periodic solutions for a delayed ratio-dependent predator-prey model with Holling Ⅲ type functional response and harvesting terms[J]. Journal of Mathematical Analysis & Applications,2010,365(2):524-540.

[5] FAN H. Multiple positive periodic solutions for a food-limited two-species Gilpin-Ayala competition patch system with periodic harvesting terms[J]. Journal of Inequalities & Applications,2012,291(1):1-17.

[6] 刘子珍,刘秀湘. 具有迁移效应和收获率的Hassell-Varley-Holling捕食者-食饵系统的周期解[J]. 华南师范大学学报(自然科学版),2014,46(2):10-16.

LIU Z Z,LIU X X. Periodic solutions in a Hassell-Varley-Holling predator-prey system with dispersal and harvest[J]. Journal of South China Normal University(Natural Science Edition),2014,46(2):10-16.

[7] ZHANG T,WEI T. Multiplicity of positive almost periodic solutions in a delayed Hassell-Varley-type-predator-prey model with harvesting on prey[J]. Mathematical Methods in the Applied Sciences,2014,37(5):686-697.

[8] MENG X Z,CHEN L S. Almost periodic solution of non-autonomous Lotka-Volterra predator-prey dispersal system with delays[J]. Journal of Theoretical Biology,2006,243(4):562-574.

[9] ZHU H G,WANG K,LI X J. Existence and global stability of positive periodic solutions for predator-prey system with infinite delay and diffusion[J]. Nonlinear Analysis:Real World Applications,2007,8(3):872-886.

[10] LIU X X,HUANG L H. Permanence and periodic solutions for a diffusive ratio-dependent predator-prey system[J]. Applied Mathematical Modelling,2009,33(2):683-691.

[11] XU C J,ZHANG Q M. Dynamical behavior of a delayed diffusive predator-prey model with competition and type III functional response[J]. Journal of the Egyptian Mathe-matical Society,2014,22(3):379-385.

[12] SHI H B,LI Y. Global asymptotic stability of a diffusive predator-prey model with ratio-dependent functional response[J]. Applied Mathematics and Computation,2015,250:71-77.

[13] 何崇佑. 概周期微分方程[M]. 北京:高等教育出版社,1992.

[14] LI Y K,YE Y. Multiple positive almost periodic solutions to an impulsive non-autonomous Lotka-Volterra predator-prey system with harvesting terms[J]. Communications in Nonlinear Science and Numerical Simulation,2013,18(11):3190-3201.

[15] GAINES R E,MAHWIN J L. Coincidence degree and nonlinear differential equations[M]. Berlin:Springer,1977.

[16] 刘玉琏,傅沛仁,林玎,等. 数学分析讲义[M]. 5版. 北京:高等教育出版社,2008.

Eight Positive Almost Periodic Solutions for Diffusive Predator-Prey System with Harvesting Terms

YAO Xiaojie*, QIN Fajin

(College of Mathematics and Computer Science, Guangxi Science & Technology Normal University, Laibin 546199, China)

A kind of diffusion predator-prey systems with Hassell-Varley functional responses and harvesting terms is proposed. By using a continuation theorem based on coincidence degree theory and inequality analysis, eight possible cases of the prior boundary of the solution of the system are analyzed in detail, and the sufficient conditions of least eight positive almost periodic solutions of the system are established.

harvesting terms; Hassell-Varley functional responses; diffusive predator-prey system; eight positive almost periodic solutions; coincidence degree

2016-03-25 《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

广西壮族自治区自然科学基金项目(2013GXNSFAA019022)；广西壮族自治区高校科学技术研究项目(2013YB282，YB2014468)

*通讯作者:姚晓洁，副教授，Email:yaoxiaojie1970@163.com.

O175.7

A

1000-5463(2017)06-0107-06

【中文责编：庄晓琼 英文审校：叶颀】