现代数学视角下的NIM型游戏
2017-12-24王姿婷李建华
王姿婷 李建华
(1 海南省文昌中学 571300;2北京师范大学数学科学学院 数学与复杂系统教育部重点实验室 100875)
1 前言
与众多经典的数学游戏一样,NIM型游戏的趣味性与挑战性如此浓厚,以至于得到各领域数学研究者及爱好者的关注,首先它作为博弈游戏的一员,在博弈论、图论中常被提及,它在集合论、组合数学中也占据较重要的位置.众多相关文献或声势浩大的占据整章的篇幅(如法国数学家C.Berge所著的《The Theory of Graphs and Its Applications》专门在第六章对NIM型游戏对策的研究),或将游戏隐匿在浩繁的文字中,对游戏与相关理论了解不够深入者,多会因其近乎纯数学的严肃外表看不真切NIM型游戏的轮廓.下面,我们对现代数学视角下NIM型游戏做一个导引式的介绍与分析.
2 NIM型游戏
2.1 NIM型游戏与图论
Sprange-Grundy值介绍
包括经典NIM游戏在内的许多的NIM型游戏,通常可以用一种称之为“Sprange-Grundy值”予以分析,所谓的“Sprange-Grundy值”实际上是一种状态函数:
SG(p,q,…,r)=f(p,q,…,r)
例如经典NIM游戏中石子全部被取完的状态的“Sprange-Grundy值”为SG(0,0,…,0)=0.我们规定:凡使“Sprange-Grundy值”为0的状态为平衡状态.
假定甲将局势拿取成了(p,q,…,r),而SG(p,q,…,r)>0,接下来轮到乙拿取,如乙拿取成了(p′,q′,…,r′),如果乙有办法让SG(p′,q′,…,r′)=0,那么乙就占据了平衡状态这一有利局势,接下去乙步步为营,每次都占据平衡状态,直至状态变为(0,0,…,0).
当然,f(p,q,…,r)函数不特指哪个函数,不同的游戏有不同的SG(p,q,…,r)求法,而函数f(p,q,…,r)的选取有相当的技巧.例如:
在堆数为1的经典NIM游戏中(有一堆石子,数量为n,甲乙两人轮流从这堆石子中取走一些石子 ,每人每次最多取走m个(m 在堆数大于1的经典NIM游戏中,也可知此时函数f(p,q,…,r)应选取为f(p,q,…,r)=(p,q,…,r)Nim,此处的(p,q,…,r)Nim即为先前定义过的“NIM和”. “穆尔”游戏中(与NIM游戏的规则基本相同,唯一有区别的地方是:玩家的每一步,可以从任意不超过k堆中取石子),类似于NIM游戏,函数f(p,q,…,r)应选取为f(p,q,…,r)=(p,q,…,r)Nim k,而这里的(p,q,…,r)Nim k就是先前定义过的“NIMk和”. 与图论的联系分析 首先,在图论中,我们可以将经典NIM游戏中的每一局势看做一个顶点,而每一个顶点与其后继局面的顶点以边相互连接,这样一来,从初始局势开始,所有的局面就构成了一个由若干个顶点以及连接这些顶点的有向边所组成的图,并且,每两个顶点之间至多可以有一条有向边将它们连接起来.将所有的顶点集合记为P,所有的有向边集合记为E,则整个游戏的所有状态组合起来便可对应一个有向图G(P,E).若有一条有向边e0,从p0出发,指向p1,则p0与p1是邻接的,且称p1为p0的后继顶点,对于某个顶点pi∈P,记其所有后继顶点的集合为H(pi). 事实上,这些顶点与之前的局势数组是一一对应的,例如(a1,a2,…,ai,…,an)是某一个局势,而且后继顶点即为(a1,a2,…,bi,…,an)便为它的一个可以指向的局势,其中bi 回到图中讨论游戏,若当前的局面为顶点p0,下一位游戏者只能在H(p0)中选择一个顶点,而H(pj)=∅即为游戏结束的标志,在经典NIM游戏以及其他不允许不进行任何操作的NIM型游戏中,这个图的任意一条边所关联的两个顶点不可能重合,即不会出现环. 显然,寻找游戏的平衡状态,就转变成了寻找图中这样一个顶点集W⊂P,它满足: (1)若pi∈W,则H(pi)∩W=∅; (2)若pi∉W,则H(pi)∩W≠∅. 第一条性质对应着“必破性”,第二条性质对应着“还原性”.此时的“Sprange-Grundy值”可按以下方式计算:首先定义一个函数SG(x),它是图的顶点集P到非负整数集N的一个映射,此时的SG(pi)=mex{SG(pj)|pj∈H(pi)},其中mex(K)=min{d|d∈N∧d∉K},若H(pj)=∅则SG(pj)=0.可以看到,这个函数SG(x)是一个递归函数. 由之前的分析我们知道,经典NIM游戏的图中一定会有顶点集W的存在,而且W={pi|SG(pi)=0},这是因为,从SG(pi)定义中所用的函数mex(K),我们可以知道,若SG(pi)=0,则任意一个后继顶点pj∈H(pi),都有SG(pj)≠0,即H(pi)∩W=∅成立,且若SG(pj)≠0,定是由于存在pj的一个后继顶点pk∈H(pj),使得SG(pk)=0,即H(pj)∩W≠∅成立.这样一来,只需依次占据顶点pi和pj,并在之后如法炮制即可在步数有限时取得胜利. 此处例举局势(1,2,3)的“Sprange-Grundy值”的计算过程,以便于读者对上述函数SG(x)的理解.首先我们按照自然顺序,逐一建立如下的图的顶点与局势数组之间的对应: p1→(0,0,0),p2→(0,0,1),p3→(0,1,1),p4→(0,0,2),p5→(0,1,2),p6→(1,1,1),p7→(1,1,2),p8→(0,2,2),p9→(1,2,2),p10→(0,0,3),p11→(0,1,3),p12→(0,2,3),p13→(1,1,3),p14→(1,2,3). 可以推知各顶点的后继顶点集合为: H(p1)=∅;H(p2)={p1};H(p3)={p2}; H(p4)={p1,p2};H(p5)={p2,p3,p4};H(p6)={p3};H(p7)={p3,p5,p6};H(p8)={p4,p5};H(p9)={p5,p7,p8};H(p10)={p1,p2,p4};H(p11)={p2,p3,p5,p10};H(p12)={p4,p5,p8,p11};H(p13)={p3,p6,p7,p10,p11};H(p14)={p5,p7,p9,p11,p12,p13}; 这些顶点所构成的有向图,局部如图1所示,完整图见图2,可见这样对应出来的图是没有有向回路的,可以看出,这是一个连通的有向图,但不是强连通的. 图 1 图 2 因为SG(p1)=0,故 SG(p2)=mex{SG(p1)}=mex{0}=1, SG(p3)=mex{SG(p2)}=mex{1}=0, SG(p4)=mex{SG(p1),SG(p2)} =mex{0,1}=2, SG(p5)=mex{SG(p2),SG(p3),SG(p4)} =mex{1,0,2}=3, SG(p6)=mex{SG(p3)}=mex{0}=1, SG(p7)=mex{SG(p3),SG(p5),SG(p6)} =mex{0,3,1}=2, SG(p8)=mex{SG(p4),SG(p5)} =mex{2,3}=0, SG(p9)=mex{SG(p5),SG(p7),SG(p8)} =mex{3,2,0}=1, SG(p10)=mex{SG(p1),SG(p2),SG(p4)} =mex{0,1,2}=3, SG(p11)=mex{SG(p2),SG(p3),SG(p5),SG(p10)}=mex{1,0,3,3}=2, SG(p12)=mex{SG(p4),SG(p5),SG(p8),SG(p10),SG(p11)}=mex{2,3,0,3,2}=1, SG(p13)=mex{SG(p3),SG(p6),SG(p7),SG(p11)}=mex{0,1,2,2}=3, SG(p14)=mex{SG(p5),SG(p7),SG(p9),SG(p11),SG(p12),SG(p13)}=mex{3,2,1,2,1,3}=0. 观察各顶点的“Sprange-Grundy值”,为0的顶点所对应的局势,正好是之前所分析过的有利局势,而剩余的都是不利局势,其“Sprange-Grundy值”都不为0! 值得一提的是,Sprange-Grundy函数是为了研究NIM而引入的,但之后的发展,远不止NIM本身的内涵性诠释.其中SG-组合游戏[注]贾志豪.组合游戏略数—浅谈SG游戏的若干拓展及变形[J]国家集训队2009论文就是其一. SG-组合游戏的介绍 这类游戏若有如下特征便可称为SG-组合游戏: •游戏有两个参与者,记为A和B,二者在游戏过程中轮流作出决策; •游戏的所有位置构成集合P,游戏的规则为由P→P的多值映射H; •同一个游戏位置,不可能多次到达; •当一方无法作出决策时游戏结束,且判决输赢,游戏不会出现平局. 这类游戏都可以用Sprange-Grundy函数进行解决.若同时进行多个SG-组合游戏,它们的总和也构成了一个SG-组合游戏,它包含多个单一的游戏,游戏者可以任意挑选其一进行决策,换个意义说,这些单一的游戏成了总游戏的子游戏. 对应到图论中,我们就可以将总的SG-组合游戏对应为总图G(P,E),各个子游戏的图Gi(Pi,Ei)便为总图G(P,E)的分支,总图G(P,E)的分支数就为它所包含的单一游戏的数目. 总游戏的Sprange-Grundy函数值就是各个子游戏的Sprange-Grundy函数值的异或和:SG=SG1⊕SG2⊕…⊕SGn. Sprange-Grundy函数值在以最终谁拿完算赢的游戏中的使用方式之前已讨论,现在借此函数再研究以最终取完为输的SG-组合游戏,之前研究过以取完为输的经典NIM游戏,此处推而广之到所有符合定义的SG-组合游戏,当然,此时游戏规定,决策集合为空的游戏者胜利. 我们直接介绍由贾志豪给出的结论SJ定理: 在决策集合为空的游戏者算胜利的SG-组合游戏中,先手必胜当且仅当: (1)总游戏的Sprange-Grundy函数值不为0且游戏中某个单一游戏的Sprange-Grundy函数值大于1; (2)总游戏的Sprange-Grundy函数值等于0且游戏中没有一个单一游戏的Sprange-Grundy函数值大于1. 该定理的论证过程不在本文讨论范围,感兴趣的读者可自行查阅. 回头看看这些游戏描述及策略分析,经典NIM游戏原有的面貌已全然看不出来,这俨然只是图论中一些决策游戏!但是其实我们如果考虑到,经典NIM游戏中允许的操作是从一堆中拿走一定量的石子,那么,k堆的经典NIM游戏共同构成的总游戏所对应的图就可以看成每一堆自成的图的累加了,也就是说,总图可以划分为k个子图的合成,即分别拥有顶点集P1,P2,…,Pk的图G1,G2,…,Gk做直和组成了k堆NIM游戏的总图,其中,总图的顶点集 P={(p1,p2,…,pk)|pi∈Pi,1≤i≤k}; 边由其后继H(P)={(p1,p2,…,pi,…,pk)|pi∈H(Pi),1≤i≤k}可以给出;符号记作是G=G1⊕G2⊕…⊕Gk,由之前的定义,我们可以知道,这也是一个NIM型游戏.另外,许多基于图上的操作游戏如删边游戏,也能与NIM型游戏产生联系. 观察到,在堆数为3的经典NIM游戏中,每三个数构成一个的数组,更特殊的是,在所找出的制胜策略里头,任意一对数字都能出现且只出现在一个三元数组里头!这不禁让我们想起设计指标λ=1的区组设计,又因为每一组的元素个数k=3,这俨然就是一个Steiner三元系统(STS)!而制胜策略中的三元系统的构造,就是之前所循的“NIM和”为0的方法! 可以指出的是,指标λ=1的STS(v)中,由于任意两个数该STS(v)的一个数组中总能出现且只出现一次,故某一三元组已存在在该STS(v)中,若在该区组中改变任意一个数,则必跳出此STS(v);若某一三元组不属于该STS(v),我们也总能通过适当减小当中某一个数使其又回到该STS(v)中!从这个意义上说,我们总能通过一定的方法,找到最大石子数不超过v=2n-1(n≥2)的“抓三堆”与STS(v)之间的对应!从而将3堆情形下的经典NIM游戏的制胜策略问题转化成了组合数学中STS(v)的区组设计问题!当然,并不是所有的STS(v)都能够对应上NIM的制胜策略,例如包含区组(1,2,4)的STS(v)就不是制胜策略了,因为这个STS(v)不可能再包含(1,2,3). Kirkman女生问题的介绍 Kirkman在1850年提出了著名的女生问题:十五个女生站成每排三人的五排,每排的三人互为伙伴,问能否安排一种排队方法,使得连续七天内,每个人的两个伙伴都不会重复.这就是后来被不少数学家关注且研究的Kirkman女生问题,后来,数学家们还将人数进行了一般化的处理,使人数为v=6n+3的形式,一般化后的问题又称为Kirkman三元系问题,它是这样的Steiner三元系统(STS):它的区组可以分解为若干个可解类,使得每一个元素恰好出现在每个可解类的一个区组中,称这样的(STS)是可解的. 这里,需要令v=6n+3,而不能是v=6n+1,是因为,在每个可解类中,必须包含所有元素,因此,v必须是3的倍数,故只能是v=6n+3.我们看Kirkman给出的一个解: 星期一:{1,2,3},{4,8,12},{5,10,15},{6,11,13},{7,9,14}; 星期二:{1,4,5},{2,8,10},{3,13,14},{6,9,15},{7,11,12}, 星期三:{1,6,7},{2,9,11},{3,12,15},{4,10,14},{5,8,13}; 星期四:{1,8,9},{2,12,14},{3,5,6},{4,11,15},{7,10,13}; 星期五:{1,10,11},{2,13,15},{3,4,7},{5,9,12},{6,8,14}; 星期六:{1,12,13},{2,4,6},{3,9,10},{5,11,14},{7,8,15}; 星期天:{1,14,15},{2,5,7},{3,8,11},{4,9,13},{6,10,12}. 我们看到,这个解恰好是我们经典NIM游戏中k=3且每一堆石子数都不超过15的情况下的平衡状态! 这里,我们可以证明:v=2n-1(n≥2)且3|v时(即n为偶数时)的Steiner三元系统的区组可以如下构造: 罗见今老师的一本册子中较为细致地做了这部分的一些整理工作[注]罗见今.科克曼女生问题(世界数学名题欣赏丛书)[M].沈阳:辽宁教育出版社,1995.,故若想在这一方面做进一步的研究,可以自行参阅. 两个集合做对称差,求的是属于且只属于其中的一个集合的元素,所构成的集合,相当于两个相对补集的并集,或者是两个集合的交集在它们并集中的补集,即: A△B=(AB)∪(BA)=(A∪B)(A∩B). 对称差运算满足交换律和结合律: A△B=B△A, (A△B)△C=A△(B△C)=A△B△C. 交换律的证明显然,结合律的证明就显得稍微复杂一些. 证明(结合律) A△(B△C)=(A(B△C))∪((B△C)A) 同理可证: 故有,结合律成立,证毕. 那么,这与“NIM和”之间的具体关系是什么? 1.若(a′,b,c)、(a,b′,c)和(a,b,c′)都是有利局势,则有: (a′>a)∧(b′>b)⟹c′ 这其实可以通过下面的维恩图观察出来: 图3 图4 图5 其中,图3中,A′为四边形CDEF,B为四边形HIJK,由于A′△B△C=∅,故C即为图中的四边形CHKF与四边形DIJE的并;又因为A△B′△C=∅且A′>A,B′>B,C=C,故A′比A大的部分应该恰好与B′比B大的部分重合,且落在C中,如见图4中的圆⊙C1;如此一来,当C′想要满足A△B△C′=∅,就必将比C少掉圆⊙C1的部分,见图5. 2. (a,b,c)中任意一元不大于另两元之和,且不小于另两元之差. 证明这一结论可由A△B△C=∅得到,若其中一元含有另外两元所不含的元素,它们的对称差不可能为空集,前半句得证;同理,可知两元之差也必含与第三元中,后半句得证. 3.若(a,b,c)是有利局势,且有2t-1≤a<2t,那么(a,b+k·2t,c+k·2t)也是有利局势,其中k是自然数. 证明b和c这两元同时加上同一个k·2t之后,转为2的方幂的集合B′与集合C′就同时多了相同的元素,多的这些都存在两个集合的交集之中,恰好能够在对称差B′△C′运算中消掉,又因为2t-1≤a<2t,故加上的这个数又在与A做对称差运算时不带来实质性的消减影响.故A△B′△C′=∅也同样成立. “必破性”:利用性质1我们可以知道,若在有利局势(a′,b,c)中,从某一堆中拿走一些石子,不妨假设从第一堆中取走若干石子,使其变成了(a,b,c),那么此时它就不是有利局势了,否则由于(a,b′,c)也是有利局势,由性质1可推出c “还原性”:从有利局势取至不利局势如(a,b,c)后,在余下的某一堆中恰可以取走适当的石子,使之变为有利局势,此时可取为(a,b,c′). 另外,利用性质3,我们便可以从一个已知的简单平衡状态出发,构造出更多的平衡状态,如已知(1,2,3)是平衡状态,那么(1,2k,2k+1),(1,4k+2,4k+3),(4k+1,2,4k+3),(16k+1,2,16k+3),(32k+1,32k+2,3)等等也都是.并且,有理由相信,每一个平衡状态都可以看成是一些简单初始状态经过若干次的双元同加一个数这样的变化所得到的,这些简单的初始状态构成一个集合S,它们在性质3的运算下将能够生成整个平衡状态集.而这个初始集合S就是{(0,0,0)},它只有一个元素. 例如: 事实上,由于所有的平衡状态都满足三个集合的对称差能够为0,意味着某一个2的方幂若出现,必只在其中两个集合中出现,这样一来,在递推过程中,我们就总能倒着两两删除这个数,最后一步一步倒推回最初的生成元(0,0,0),这使我们不禁想起经典NIM游戏里面的情景,它几乎是游戏情形的再现. 上述的几种数学理论中,NIM型游戏的轮廓有时尚可依稀分辨,但有些已全然看不出其原貌,已升华为纯数学的抽象语言了.而NIM型游戏在数学中的研究,远不止前面所提及的这些,例如利用“NIM和”研究得到的新成果,可以与高斯函数、莫比乌斯函数、伽罗华域、欧几里得环等相联系④,也是令人感到惊奇的.数学中总是有着一些意料之外却又在情理之中的联系,让你不得不叹服那些发现这些联系的数学家们,在布满荆棘的丛林中,天才的探险家与常人不同的是,他们总能披荆斩棘,发现暗藏其中的巨大宝藏,为世人带来传奇与快乐! ④ 罗见今.Nim—从古代的游戏到现代的数学[J].自然杂志,1986,01.

2.2 NIM型游戏与组合数学三元系
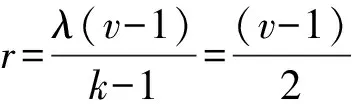

2.3 NIM型游戏与集合论


















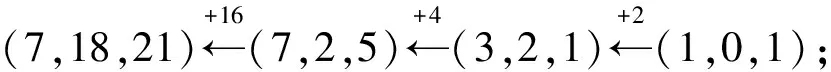



3 结束语
