Pidong WANG,Jianguo ZHANG,Hao ZHAI,Jiwei QIU

School of Reliability and Systems Engineering,Beihang University,Beijing 100083,China

Science and Technology on Reliability and Environment Engineering Laboratory,Beihang University,Beijing 100083,China

A new structural reliability index based on uncertainty theory

Pidong WANG,Jianguo ZHANG*,Hao ZHAI,Jiwei QIU

School of Reliability and Systems Engineering,Beihang University,Beijing 100083,China

Science and Technology on Reliability and Environment Engineering Laboratory,Beihang University,Beijing 100083,China

The classical probabilistic reliability theory and fuzzy reliability theory cannot directly measure the uncertainty of structural reliability with uncertain variables,i.e.,subjective random and fuzzy variables.In order to simultaneously satisfy the duality of randomness and subadditivity of fuzziness in the reliability problem,a new quantification method for the reliability of structures is presented based on uncertainty theory,and an uncertainty-theory-based perspective of classical Cornell reliability index is explored.In this paper,by introducing the uncertainty theory,we adopt the uncertain measure to quantify the reliability of structures for the subjective probability or fuzzy variables,instead of probabilistic and possibilistic measures.We utilize uncertain variables to uniformly represent the subjective random and fuzzy parameters,based on which we derive solutions to analyze the uncertainty reliability of structures with uncertainty distributions.Moreover,we propose the Cornell uncertainty reliability index based on the uncertain expected value and variance.Experimental results on three numerical applications demonstrate the validity of the proposed method.

©2017 Production and hosting by Elsevier Ltd.on behalf of Chinese Society of Aeronautics and Astronautics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1.Introduction

Reliability analysis has been a hot research topic in recent years,as the influences of uncertainty arising on loads,material properties,dimensions,and geometries become more and more profound.1This topic has a wide range of applications in the design and analysis of structural systems for aerospace vehicles,civil engineering,and manufacturing industry.2

Probability theory is one of the most classical and prevailing tools in dealing with uncertain variables,which has been widely used to estimate structural reliability and safety by calculating the probability of failure and the reliability index β,2–5and a lot of probabilistic reliability methods have been proposed in literature such as the first-order method,2,5,6the second-order method,2,6the response surface method,7,8and the numerical sampling simulation method.7,9

However,in practical structural engineering,beside randomness which can be modelled by probabilistic theory with Probability Distribution Functions(PDFs)3,9,10we encounter epistemic uncertainty,3,10caused by things such as loss of information,limited knowledge,and inevitable man-made mistakes.3,11,12It cannot be well explained by randomness and probabilistic models.Although,for uncertain problems in structural engineering,a random variable is always employed to represent a kind of subject probability,which is conducted by experts’judgments(subjective interpretation),10the uncertainty of this variable is actually fuzziness from experts’judgements.3In this sense,that results in a juxtaposition with randomness.3,11As a consequence,fuzzy variables and credibility theory are introduced to describe fuzziness with Membership Functions(MFs).3,9,13A new definition for structural reliability index based on credibility theory is explored,which is named‘Cornell fuzzy reliability index”.3This index and the credibility offailure are calculated based on the possibilistic principle instead of the probabilistic one.3,9,14,15Nevertheless,in most practical situations,some input parameters of structures might be represented with PDFs and some with MFs.9For completeness,different knowledge conditions for each uncertainty parameter derive ‘hybrid” uncertain variables in structural reliability analysis.3Therefore,in order to comprehensively analyze the reliability of structures correctly,subjective randomness and fuzziness should be jointly considered,resulting in a hybrid model with random and fuzzy variables.3,9,15,16

Many approaches have been proposed to solve the aforementioned hybrid reliability problems in structures.Most of them separate random and fuzzy parameters based on a double-sampling framework,9such as the Monte Carlo(MC)method,17improved sampling methods,18transformationbased methods,19,20and the iteration method.21To avoid the deterioration of efficiency and accuracy,several works have attempted to combine stochastic expansions with traditional optimization methods.9,22–26They are mainly concentrated on explaining fuzzy variables by adopting the probability theory,13and calculating the probability of failure and the structural reliability index β based on a probability measure.2,5However,the probability measure with additivity used by these methods fails to satisfy the subadditivity axiom of fuzziness,and the possibilistic measure cannot satisfy the duality axiom of randomness.10,15To that end,it is suggested that a reliability quantification model based on probability theory and one based on credibility theory frequently yield infeasible solutions with large differences and paradoxical results.1,5,10In other words,neither probability theory nor credibility theory can deal with structural reliability problems under epistemic uncertainty with hybrid subjectiverandom and fuzzy variables,1,3,15,27,28because neither measure of the two theories can satisfy duality and subadditivity simultaneously.10,15,27,28

In order to achieve a reasonable solution to these structural reliability problems,solving the limitations of the two measures,we introduce the uncertainty theory and an uncertain measure proposed by Liu15,27,28in structural reliability,including the normality,duality,subadditivity,and product axioms.This theory relies on the uncertain measure to describe the belief degrees of events affected by epistemic uncertainty.15,27Liu firstly employed it in system reliability and defined reliability index as a measure of systems’reliability.10,29This theory provides a concrete mathematical description on different types of uncertain parameters in the uncertainty space.15The‘belief degree”in the range of[0,1]is adopted to represent the level of confidence about the occurrence of a particular event5in engineering structures.Belief reliability was defined by Zeng et al.as the uncertainty measure of a system to perform specified functions within given time under given operating conditions.10,30Based on the new theory,this paper will explore a new reliability index and quantification model,and discuss how to apply them to quantify the reliability of structures with the hybrid uncertainty problem.The main contributions of this paper lie in the following two-folds:

(1)In the framework of the uncertainty theory,the new reliability index and quantification model are based on the uncertain measure instead of a probabilistic or possibilistic one.

(2)We uniformly treat subjective random and fuzzy parameters as uncertain variables in the uncertainty space.Based on the new theory and variables,a new definition and formulations are proposed to deal with epistemic uncertainty,especially for the two parameters mixed,simultaneously in structural reliability problems.With the proposed formulations,not only the duality of randomness can be described,but also the subadditivity of fuzziness can be explained.

The remainder of this paper is organized as follows.In Section 2,some useful concepts in the uncertainty theory are illustrated in Section 2.1 such as uncertain measure,uncertain variable,and uncertainty distribution.Subsequently,in Section 2.2,based on the uncertain measure and uncertainty distributions,we prove two important theorems(Theorems 2 and 3)and derive formulas to quantify the uncertainty reliability and the uncertainty offailure with the limit state function of structures.According to the similarity between formulations based on the uncertain measure and the presented probabilistic one,the ‘Cornell uncertain reliability index” is defined by the uncertain expected value and variance in Section 3.Finally,three numerical applications to demonstrate its rationality and practicability are presented.Firstly,reliability analysis for strengths of materials is used to prove that these methods are effective and accurate,and to analyze the relationship between the Cornell uncertainty reliability index and uncertainty reliability,due to low analytical complexity of the linear limit state function.Secondly,the methods are applied to deal with the reliability problem in a real structure,in this specific case a beam structure.

2.Uncertainty quantification for structural reliability

2.1.Overview of uncertainty theory

Definition 1(Uncertain measure15).Let(Γ,L)be a measurable space.For ∀Λ ∈ L,the element Λ is called a measurable set.Then,the set functionMis called an uncertain measure ifit satisfies the following four axioms:

Axioms1(Normalityaxiom).FortheuniversalsetΓ,M{Γ}=1.

Axioms 2(Duality axiom).For ∀Λ,M{Λ}+M{ΛC}=1,where ΛCis the complement set of Λ.

Axioms 3(Subadditivityaxiom).For every countable sequence of events Λ1,Λ2,...,we have

Axiom 4(Product axiom).Let(Γk,Lk,Mk)be uncertainty spaces and Λkbe events from Lkfork=1,2,...,respectively.

The product uncertain measureMis an uncertain measure if

Definition 2(Uncertainty space15).Assume that Γ is a nonempty set,L is a σ -algebra over Γ,andMis an uncertain measure.Then the triplet(Γ,L,M)forms an uncertainty space.This space is called complete,if the following conditions hold:

(1)M{Λ1}=M{Λ2}for∀Λ1,Λ2∈ L.

(2)For any subset A,if Λ1⊂ A⊂Λ2,then A⊂Ω,and M{Λ1}=M{A}=M{Λ2}.

Definition 3(Uncertain variable15).Let ξ be a measurable mapping function from an uncertainty space(Γ,L,M)to the set of real numbers.Then,ξ is called an uncertain variable.If ξ1,ξ2,...,ξnare uncertain variables,andfis a real valued measurable function,thenf(ξ1,ξ2,...,ξn)is also an uncertain variable,and can be written as

Then ξ1,ξ2,...,ξnare independent if and only iffor any Borel setsB1,B2,...,Bnof real numbers.15,31For a set of independent uncertain variables ξ1,ξ2,...,ξn,iff1,f2,...,fnare measurable functions,thenf1(ξ1),f2(ξ2),...,fn(ξn)are independent.28

Actually,an uncertainty distribution is commonly used to describe an uncertain variable, defined by Liu15as Φ(x)=M{ξ≤x}for any real numberx.Moreover,Φ(x)is regular ifit is a continuous and strictly increasing function forxwith 0＜Φ(x)＜1,andΦ(x)=1.28In this case,the inverse function Φ-1(α)is defined as the inverse uncertainty distribution of ξ.28It is suggested that the distributions are a carrier of incomplete information of uncertain variables.15For both subjective random variables and fuzzy ones,we can utilize uncertain variables and uncertainty distributions to describe them in the uncertainty space.15,27,28,31

Definition 4(Uncertain expected value15).Let ξ be an uncertain variable.Then the expected value of ξ is defined as

whereE(·)is the uncertain expected value operator.

In addition,Liu28has proven the linearity of the expected value operator,and proposed that if there is an uncertainty distribution Φ(x)with ξ,then Eq.(4)turns into the following:

Moreover,if Φ(x)is regular,then Eq.(4)will be rewritten28as

Definition 5(Uncertain variance15).Let ξ be an uncertain variable with a finite expected valuee.Then the variance of ξ is

whereV(·)is the uncertain variance operator.

Similarly,if there is an uncertainty distribution Φ(x)with regard to ξ,then Eq.(7)turns into28

Moreover,if Φ(x)is regular,then the following equation holds32:

Theorem 115.Letξ1,ξ2,...,ξnbe independent uncertain variableswithcontinuousuncertaintydistributionsΦ1,Φ2,...,Φn.Iff(ξ1,ξ2,...,ξn)is strictly increasing forξ1,ξ2,...,ξkand strictly decreasing forξk+1,ξk+2,...,ξn,thenξ =f(ξ1,ξ2,...,ξn)has the following uncertainty distribution:

Moreover,if Φ1,Φ2,...,Φnare regular uncertainty distributions,then

where λ satisfies the following equation29:

Considering the monotone functionf(ξ1,ξ2,...,ξn)of the independent uncertain variables ξ1,ξ2,...,ξnwith regular uncertainty distributions Φ1,Φ2,...,Φn,which is strictly increasing for ξ1,ξ2,...,ξkand strictly decreasing for ξk+1,ξk+2,...,ξn, the uncertain expected value of ξ =f(ξ1,ξ2,...,ξn)can be obtained as follows33:

The uncertain variance of ξ =f(ξ1,ξ2,...,ξn)with the uncertain expected valueecan be calculated by32

2.2.Uncertainty reliability and uncertainty of failure

With the limit state function of structures under epistemic uncertainty,we redefine structural uncertainty reliability based on the uncertain measure15and belief reliability30as follows.

Definition 6(Structural uncertaintyreliability).Given an uncertainty space(Γ,L,M),without loss of generality,we consider the basic problem in structural reliability,containing only one generalized stressSresisted by one general strengthR.BothSandRare independent uncertain variables.Let the limit state functionG=R-S,whereG=R-S＞0 indicates the state of being safe,andG=R-S≤0 indicates the state of being failure.Then the uncertainty of occurrence of a failure event is defined as

From the duality axiom of the uncertainty theory,the uncertainty reliability of a structural system where

G=R-S＞0 can be formulated as

Following the probability of reliability,we denoteMreliabilityas the ‘structural uncertainty reliability” to quantify the uncertainty of a safe or failure event in a structural system with the numerical value of[0,1],andMfailuredescribes the confidence how we believe the occurrence of a failure event.It is clear that due to the similarity with the probability of failure and reliability,the numerical value ofMhas been used to represent the confidence with which it is believed that the event will occur instead of ‘frequency”.WhenMfailure=1(Mreliability=0),it means that we completely believe the failure event will happen and the event of structural reliability is completely impossible.When the failure event and its complementary(reliability)event are equally likely,thenMreliability=Mfailure=0.5.The higherMreliabilityis,the more strongly we believe the reliability event will happen.

If the uncertainty distribution ΦGis given,the failure uncertainty with Eq.(15)can be obtained by

Meanwhile,the structural uncertainty reliability Eq.(18)turns into

Remark 1.In case when ΦSand ΦRare provided and ΦGis unknown,we establish a model for solving the uncertain reliability of a structure,as depicted in the following theorems.

Theorem 2.If both R and S have continuous uncertainty distributions denoted byΦRandΦS,respectively,then the uncertaintyof failure and uncertainty reliability of a structure system can be calculated as

Proof.It is not difficult to see the functionG(R,S)=R-Sis strictly increasing with respect toRand strictly decreasing with respect toS.According to Theorem 1 and Eq.(10),ξGhas the following continuous uncertainty distribution ΦG(x):

Then,by the definition of the uncertainty of failure and uncertainty reliability,the following equations hold:

Theorem 3.If the uncertainty distributionΦRof R andΦSof S are regular,then the uncertainty of failure isλand the uncertainty reliability Mreliability=1- λ,whereλsatisfies the following condition:

Proof.The results can be directly derived from Theorem 1 and Eq.(12).□

Here,λ can be estimated by solving Eq.(24)via the interpolation method.15

3.Reliability index based on uncertain measure

Given a limit state functionG(R,S)=R-Sin the uncertainty space,a new reliability index can be defined by the uncertain expected value and variance operator,15which is similar to the ‘Cornell reliability index” with the probability measure.2,5It can be seen as an uncertain indicator that a failure(reliability)event will happen in the structural system.

Definition 7(Cornelluncertaintyreliabilityindex).Let(Γ,L,M)be an uncertainty space,andG(R,S)=R-Sbe the limit state function with two uncertain variablesRandS.The uncertainty reliability index γ is defined as

Remark 2.IfRandSare independent with regular uncertainty distributions ΦRand ΦS, γ can be equivalently formulated as wheree=E(G)=dα.According to the linearity of the uncertain expected value operator,28we can deduce thate=E(R)-E(S).

From the Cornell formulation of the structural reliability index,3γ can be denoted as ‘Cornell uncertainty reliability index”.Based on the uncertain measure,in order to estimate structural reliability with hybrid subjective randomness and fuzziness,it has been achieved by the subadditivity axiom of the uncertainty theory15dealing with the fuzzy parameters,and the duality axiom dealing with the random parameters.Following this way,our formulation can overcome these drawbacks in the probabilistic and possibilistic measures.It can be seen that the Cornell uncertainty reliability index γ is the same as the definition of ‘Cornell reliability index”,of which a larger γ indicates a higher belief degree on the occurrence of a reliability event.

4.Numerical experiments

4.1.Reliability problem in strengths of materials

Reliability analysis for the strengths of materials shown in Fig.1 is a fundamental reliability problem in structural systems.2,3In the viewpoint of the uncertainty theory,variables in benchmark problems usually consist of the fuzzy stressSand the random strengthR(MPa),which are treated as uncertain variables.This numerical example is used to evaluate the significance of the Cornell uncertainty reliability index and uncertainty reliability based on the expected value and variance asRchanges.

Let the limit state function beG=R-S, the

uncertainty distribution ofRbe ΦR(x1)(x1∈(-∞,+∞)),and the uncertainty distribution ofSbe

Table 1 Calculated results with different μ (σ2=25).

By using the uncertainty expected value operator Eq.(5)and the variance operator Eq.(8),we can derive that the expected value ofRis μ and its variance is σ2.Similarly,the expected value ofSis 122.5 and its variance is 210.4167.

Supposing that the variance σ2ofRis 25,the Cornell uncertainty reliability index,uncertainty offailure,and uncertainty reliability can be obtained by using different values of μ.The results are summarized in Table 1 and Fig.2.

From Fig.2 and Table 1,it can be observed that when the mean value ofRincreases with a constant variance,the trend of uncertainty reliability is consistent with that of the Cornell uncertainty reliability index.The larger the uncertainty reliability is,the higher the Cornell uncertainty reliability index will be,which takes on the same trend as the probability reliability.Intuitively,when the mean value of the strength increases with a constant variance,the probability that the stress is larger than the strength of a material(i.e.,a failure event)will decrease.Conversely,the reliability and the reliability index increase in the viewpoint of the probability theory,due to the uncertainty of the stress invariant.Similarly,as the mean value of strength increases,the belief degree about the material reliability becomes higher with an increasing value of the Cornell uncertainty reliability index based on the uncertainty theory.Therefore,the definition of the Cornell uncertainty reliability index proposed in this paper is reasonable and can partially reflect the law of structural reliability.

Following the same way,when the variance ofRincreases and the mean value is constant,the probability that the stress is greater than the strength of the material(i.e.,a failure event)will increase,and the reliability index will decrease in the viewpoint of the probability theory due to the dispersity of strength increasing.It should be consistent with the trend of the uncertainty reliability based on the uncertainty theory.To validate this intuitive observation,we calculate the trend of the uncertainty reliability by using different variances(25,36,100,and 200)with a constant mean value of 160.The results are shown in Fig.3 and Table 2.

From Fig.3 and Table 2,it can been seen that the trends of the uncertainty reliability and its index are consistent with our intuitive observations.We can therefore conclude that the uncertainty reliability and the Cornell uncertainty reliability index are able to provide constructive results in hybrid uncertain structural reliability analysis,if the uncertain variables are reasonably acceptable.They can be utilized to help designers make the most appropriate choice.Additionally,the presented reliability index can be solved for nonlinear functions.Let the nonlinear limit state function beG(x1,x2)=ex1-uncertainty distribution ofx1be Φ(x1)=(x1∈(-∞,+∞)),and the uncertainty distribution ofx2be

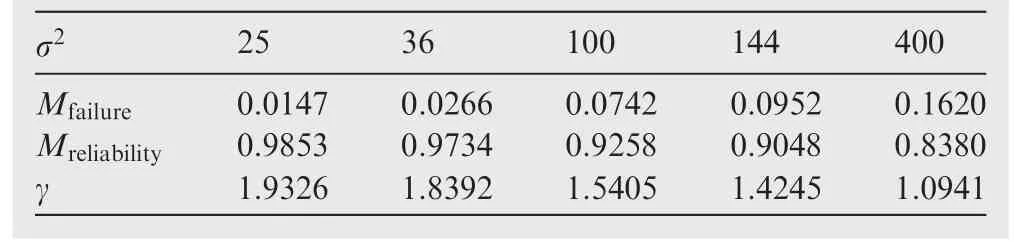
Table 2 Calculated results(μ=160).

Supposing that the variance σ2ofx1is 1,the Cornell uncertainty reliability index,uncertainty of failure,and uncertainty reliability can be obtained by using different values of μ.The results are summarized in Table 3.

To validate this intuitive observation,we calculate the trend of the uncertainty reliability by using different variances(12,1.52,and 22)with a constant mean value of 5.The results are shown in Table 4.

From the results in Tables 3 and 4,it can be seen that the trends of the uncertainty reliability and its index are also consistent with the intuitive observations.It is indicated that the presented reliability index can besolved for nonlinear functions.

4.2.Reliability analysis in a beam structure

In this numerical example,the reliability measure of a beam associated with its bending moment is calculated in Fig.4.

Table 3 Calculated results with different μ (σ2=1).

Table 4 Calculated results(μ=5).

The uncertain numerical values are summarized in Tables 5 and 6.

Here,we assume that the length of the beamL=1300 mm,beam heighth=8 mm, and the force density ρst=78.5×10-6kN/mm3.The loadFis a fuzzy variable applied at mid span as shown in Fig.4 and Table 6,and the beam breadthbis a random variable as shown in Table 5.

The bending moment at mid-span associated with random loads is subject to the following equation:

In order to analyze the reliability state of the beam,it is necessary to define the ultimate bending moment.In our work,as shown in Fig.5,the ultimate bending moment can be categorized into ‘low”,‘normal”,and ‘high” acceptable,according to the subjective judgment with incomplete test data.3

Here,

Table 5 Random variable.

Therefore,the limit state function with reference to the failure of the beam is formulated as

In more general cases,by utilizing the design ultimate bending moment and the design bending moment at mid-span as shown in Table 7,the target Cornell uncertainty reliability index γTturns out to be 1.2469,by using Eq.(26).The results are listed in Table 8.

Firstly,if the target Cornell reliability index is estimated by the probability measure,γTwill be 1.3800,greater than that based on the uncertain measure 1.2469.Thus,it will negatively affect the accuracy and belief degree of the results,when the probabilistic method is used to judge the reliability of the structure with uncertain variables.

Moreover,based on the uncertain measure-calculated results in Table 6,the reliability degree of the beam with different states for the ultimate bending moments can be obtained by the Cornell uncertainty reliability indices.For instance,when the state is ‘low”,the reliability index is less than the target one with γ=0.9837γT.It means that the state is not reliable.On the other hand,as the ultimate bending moment is changed from ‘normal” to ‘high”,the reliability increases.Specifically,when the state is ‘normal”, γ is 1.3455γT.When the state is ‘high”, γ is 1.3914γT.Therefore,the ratio γ/γTcan be assumed as ‘reliability indicator” for different states assumed by the uncertain variable ultimate bending moment.

Table 7 Random variables muand m.

Table 8 Cornell uncertainty reliability index in truss structure(γT=1.2469).

In addition,comparing γ for ‘normal” with ‘high”,they are not so much different;however,the uncertainty reliability for ‘normal” is 0.9812 and that for ‘high” is 9999.8754 × 10-4which is close to 1.In other words,the uncertainty reliability can be used to compare the reliability of a structure with different states,when the uncertainty reliability indices in different states are closely valued.

5.Conclusions

In this paper,the Cornell uncertainty reliability index and the uncertainty reliability are used to deal with epistemic uncertainty,especially for subjective randomness and fuzziness mixed in structural reliability analysis.Uncertain variables together with the limit state function are used to represent subjective randomness and fuzziness.The uncertain measure is adopted to quantify the uncertainty of failure and reliability in structures.The following conclusions can be drawn:

(1)In the framework of the uncertainty theory,we have provided an alternative interpretation of the classic reliability index,and proposed new formulations to analyze reliability in a structural system from a viewpoint of the uncertain measure.With the proposed formulations,not only the duality of random events can be described,but also the subadditivity offuzzy events can be explained.

(2)From two numerical experiments with linear and nonlinear functions,it has been proven that(a)the trend of uncertainty reliability is consistent with that of the Cornell uncertainty reliability index;(b)both of them are consistent with the ones in the viewpoint of the probability theory,respectively.

Acknowledgements

This study was co-supported by the National Natural Science Foundation of China(Nos.51675026 and 71671009)and the National Basic Research Program of China (No.2013CB733002).

1.Wang XJ,Wang L,Qiu ZP.Safety estimation of structural systems via interval analysis.Chin J Aeronaut2013;26(3):614–23.

2.Melchers RE.Structural reliability analysis and prediction.2nd ed.New York:John Wiley;1999.p.9–62.

3.Marano GC,Quaranta G.A new possibilistic reliability index definition.Acta Mech2010;210(3):291–303.

4.Rackwitz R.Reliability analysis–A review and some perspectives.Struct Saf2001;23(4):365–95.

5.Cornell CA.A probability-based structural code.J Am Concr Inst1969;66(12):974–85.

6.Breitung K.40 years FORM:Some new aspects?Probab Eng Mech2015;42:71–7.

7.Gong Q,Zhang JG,Tan CL,Wang CC.Neural networks combined with importance sampling techniques for reliability evaluation of explosive initiating device.Chin J Aeronaut2012;25(2):208–15.

8.Ren YR,Xiang JW.Crashworthiness uncertainty analysis of typical civil aircraft based on Box-Behnken method.Chin J Aeronaut2014;27(3):550–7.

9.Li LY,Lu ZZ.Interval optimization based line sampling method for fuzzy and random reliability analysis.Appl Math Model2014;38(13):3124–35.

10.Kang R,Zhang QY,Zeng ZG,Zio E,Li XY.Measuring reliability under epistemic uncertainty:Review on non-probabilistic reliability metrics.Chin J Aeronaut2016;29(3):571–9.

11.Tang J,Wu ZG,Yang C.Epistemic uncertainty quantification in flutter analysis using evidence theory.Chin J Aeronaut2015;28(1):164–71.

12.Kiureghian AD,Ditlevsen O.Aleatory or epistemic?Does it matter?Struct Saf2009;31(2):105–12.

13.Li GJ,Lu ZZ,Xu J.A fuzzy reliability approach for structures based on the probability perspective.Struct Saf2015;54:10–8.

14.Gonzalez-Gonzalez D,Cantu-Sifuentes M,Praga-Alejo R,Flores-Hermosillo B,Zun˜iga-Salazar R.Fuzzy reliability analysis with only censored data.Eng Appl Artif Intell2014;32:151–9.

15.Liu BD.Uncertainty theory.Berlin:Springer;2010.p.11–103.

16.Chakraborty S,Sam PC.Probabilistic safety analysis of structures under hybrid uncertainty.Int J Num Methods Eng2007;70(4):405–22.

17.Rao KD,Kushwaha HS,Verma AK,Srividya A.Quantification of epistemic and aleatory uncertainties in level-1 probabilistic safety assessment studies.ReliabEngSystSafety2007;92(7):947–56.

18.Li LY,Lu ZZ,Song SF.Saddlepoint approximation based line sampling method for uncertainty propagation in fuzzy and random reliability analysis.Sci China Technol Sci2010;53(8):2252–60.

19.Adduri PR,Penmetsa RC.Confidence bounds on component reliability in the presence of mixed uncertain variables.Int J Mech Sci2008;50(3):481–9.

20.Adduri PR,Penmetsa RC.System reliability analysis for mixed uncertain variables.Struct Saf2009;31(5):375–82.

21.Du XP.Unified uncertainty analysis by the first order reliability method.J Mech Des2008;130(9):1401–10.

22.Eldred MS,Swiler LP,Tang G.Mixed aleatory-epistemic uncertainty quantification with stochastic expansions and optimizationbased intervalestimation.ReliabEngSystSafety2011;96(9):1092–113.

23.Giuseppe M,Roberta S,Alba S.Reliability analysis of structures with interval uncertainties under stationary stochastic excitations.Comput Methods Appl Mech Eng2016;300:47–69.

24.Malhotra R,Singh N,Singh Y.Genetic algorithms:Concepts,design for optimization of process controllers.Comput Informat Sci2011;4(2):39–54.

25.Schue¨ller GI,Pradlwarter HJ,Koutsourelakis PS.A critical appraisal of reliability estimation procedures for high dimensions.Probab Eng Mech2004;19(4):463–74.

26.Tang ZC,Lu ZZ,Hu JX.An efficient approach for design optimization of structures involving fuzzy variables.Fuzzy Sets Syst2014;255:52–73.

27.Liu BD.Why is there a need for uncertainty theory?J Uncertain Syst2012;6(1):3–10.

28.Liu BD.Uncertainty theory:A branch of mathematics for modeling human uncertainty.Berlin:Springer-Verlag;2010.p.1–74.

29.Liu BD.Uncertain risk analysis and uncertain reliability analysis.J Uncertain Syst2010;4(3):163–70.

30.Zeng ZG,Wen ML,Kang R.Belief reliability:A new metrics for products’reliability.Fuzzy Optim Dec Making2013;12(1):15–27.

31.Liu BD.Some research problems in uncertainty theory.J Uncertain Syst2009;3(1):3–10.

32.Yao K.A formula to calculate the variance of uncertain variable.Soft Comput2015;19(10):2947–53.

33.Liu YH,Ha MH.Expected value offunction of uncertain variables.J Uncertain Syst2010;4(3):181–6.

1 June 2016;revised 7 November 2016;accepted 12 March 2017

Available online 19 May 2017

*Corresponding author.

E-mail addresses:wpd-pizi@163.com(P.WANG),zjg@buaa.edu.cn(J.ZHANG).

Peer review under responsibility of Editorial Committee of CJA.

Production and hosting by Elsevier

http://dx.doi.org/10.1016/j.cja.2017.04.008

1000-9361©2017 Production and hosting by Elsevier Ltd.on behalf of Chinese Society of Aeronautics and Astronautics.

This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

Belief degree;

Reliability index;

Structural reliability;

Uncertain measure;

Uncertain variable