浙江省春晖中学 林国夫 (邮编:312353)

基于理解的动态立体几何问题的求解

浙江省春晖中学 林国夫 (邮编:312353)

理解是数学学习的基础,脱离了理解,数学学习也就失去了灵魂,甚至会陷于形式化的教条,学习的意义也就荡然无存．因此在学习和教学中我们都应该基于理解,有意义地学习和思考,以便有效促进自身思维能力的提升．本文结合笔者自身的教学实践,通过理解性的分析来深度剖析若干动态几何的综合性问题,以展示理解在问题求解中的重要性,同时也从侧面来揭示这些问题的本源,启发读者了解和掌握解决动态立体几何中常见处理技巧和策略．

1 理解助力问题的正确求解

翻折问题作为动态立体几何问题最典型的类型,能将立体几何中的核心知识和方法融入其中,有效甄别个体的立体几何的数学素养,因此历来都受到命题者的青睐．对于翻折问题,笔者以为不管问题的呈现形式如何,在求解问题时我们都需要正确理解翻折前后间的某些不变性,借助这些不变性就可以很好地作图和分析,深入理解问题,并顺利寻求解决问题的途径．那么翻折问题我们如何去正确理解其不变性呢?

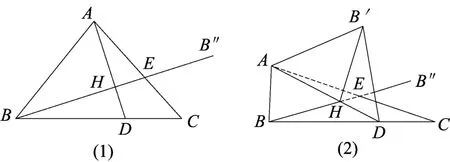
图1

空间翻折问题本质是一个局部的旋转问题,其旋转轴即为翻折的折线,因此它具备旋转的特点．如图1(1),在△ABC中,点D是线段BC上异于端点的点,将△ABD沿着AD翻折至平面AB′D,当平面ABD重合于平面ADC时,设此时点B的位置为B′,如图1(2)．要把握翻折问题,我们关键在于把握翻折中的不变量．那么在翻折中哪些量是不变的呢?显而易见的是,对于翻折的两个半平面ABD,ADC中的点、线、角等几何元素,它们的位置关系和度量值都是不变的,下面我们分析内隐性不变量．

我们过点B作AD的垂线,垂足为H,延长交AC于点E．显然在翻折过程中,BH⊥AD,EH⊥AD,故AD⊥平面BB′E,即平面BB′E⊥平面ADC．从而在翻折过程中,点B′在平面ADC内的射影始终在直线BHEB′上．此外由于在翻折过程中,BH＝B′H,故点B′在以H为圆心,半径为BH 的圆上,且圆所在平面BB′B′E与翻折线AD垂直．

从上述分析我们可以得到把握翻折过程的以下关键不变量:在翻折前的平面图形中过翻折线(图1中的直线AD)的垂线l(图1中的直线BHE),在翻折过程中,垂线l被折成的平面(图2中的平面BB′E)垂直翻折线;翻折前的任意一点P(比如点B)与翻折后对应点P′(比如点B′)的连线PP′垂直翻折线,且P′在空间的轨迹为圆．笔者认为,理解这些关键不变量对于我们把握空间翻折中的线、面位置关系非常重要．

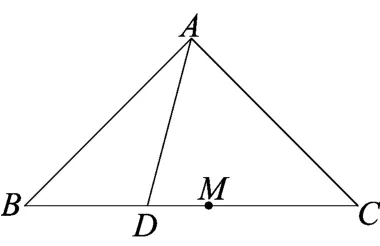
图2

例1(2017年杭州市二模)如图2,在等腰直角△ABC中,AB⊥AC,BC＝2,M为BC中点,N为AC中点,D为BC边上一个动点,△ABD沿AD翻

折至平面AB′D,使B′D⊥DC,点A 在面B′CD上的投影为点O,当点D在BC上运动时,以下说法错误的是( )

A．线段NO为定长

B．|CO|∈ [1,2)

C．∠AMO＋∠ADB′＞180°

D．点O的轨迹是圆弧

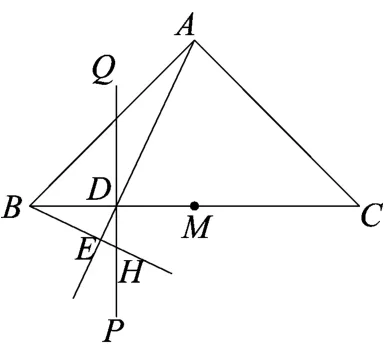
图3

解析如图3,过点B作AD的垂线,垂足为E,则对于给定的点D,△ABD沿AD翻折至平面AB′D的过程中,点B在以点E为圆心、半径为BE的圆上运动,且点B′在平面ACD内的射影在直线BE上．

图4

如图4,设点B′在平面ACD内的射影为点H,过点D作BC的垂线PQ,则点H在BE上．由于B′D⊥DC,从而DH ⊥DC,由此可知点H为BE与PQ的交点．显然由B′D⊥DC,DH⊥DC得DC⊥平面B′DH,故平面B′DH⊥平面B′DC．

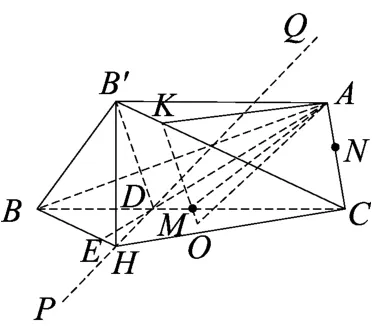
图5

为了寻找点A在面B′CD上的投影点O,我们首先需要寻找过点A的平面B′CD的垂面,考虑到平面B′DH⊥ 平面B′DC,我们只需求作过点A且与平面B′DH平行的面即可．如图5,由于AM ⊥DC,DH⊥DC,则DH//AM,再过点M作B′D的平行线交B′C于点K,从而平面AKM//平面B′DH,则点O在KM上,即只需过点A作KM的垂线,垂足即为点O．

有了上述的作图分析,下面我们可以比较方便地分析选项了．

对于选项A:由于AO⊥平面B′DC,则AO⊥OC,则在Rt△AOC中,由N为AC中点可知,从而选项A正确．

对于选项B:由于点O始终在平面AMK上,且CD⊥平面AMK,从而故OC的长|CO|最短为点C到平面AMK的距离CM＝1,最长不超过CA＝ 2,从而|CO|∈[1,2)．

对于选项D:由于在点D运动时,点O始终在固定的平面AMK上,又由于从而点O又在以点N为球心,半径为的球面Γ上运动．因此点O的轨迹是球面Γ与平面AMK相交而成的圆,故点O的轨迹是圆．

对于选项C:由于AM//DH,MO//B′D,从而∠AMO＝∠B′DH．根据线面角的最小性可知:B′D 与 平 面ACD 所 成 角 ∠B′DH ≤∠B′DE,从而180°－ ∠B′DH ≥180°－∠B′DE, 即 ∠B′DQ ≥ ∠ADB′ (又∠B′DQ＝180°－∠B′DH＝180°－∠AMO),从而180°－∠AMO≥∠ADB′,从而可得∠AMO＋∠ADB′≤180°,选项C错误．

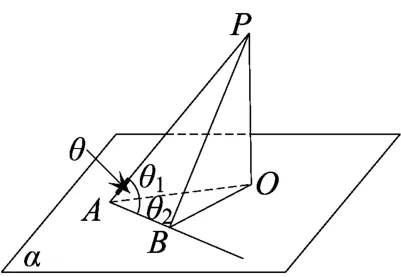
图6

在上述问题分析的过程中,我们牢牢抓住了翻折前后的不变性,从而理解了在翻折后各个空间元素的具体位置,因此也就比较准确有效地理解问题,解决问题也就水到渠成了．当然在分析过程中我们也使用了下列简单的事实:线面角的最小性．

如图6,已知直线AP是平面α的一条斜线,斜足为点A．

点P在平面α内的射影为点O,直线l是平面α内过点A的任意直线．

过点O作直线l的垂线,垂足为B．显然∠PAO是直线AP与平面α所成的角．设∠PAO＝θ1,∠OAB＝θ2,∠PAB＝θ,易得,从而cosθ＝cosθ1·cosθ2,故cosθ＝cosθ1·cosθ2≤cosθ1,考虑到且f(x)＝cosx在 [0,上单调递减,从而θ≥θ1,当且仅当θ2＝0时取等号．

由此,我们得到下述两个结果:

①cosθ＝cosθ1·cosθ2;②平面的斜线与其在平面内的射影所成角(即直线与平面所成角)是该斜线与平面内任意直线所成角中最小者．

上述两个结果对于我们理解有关线面角和异面直线所成角的最值问题非常有用．

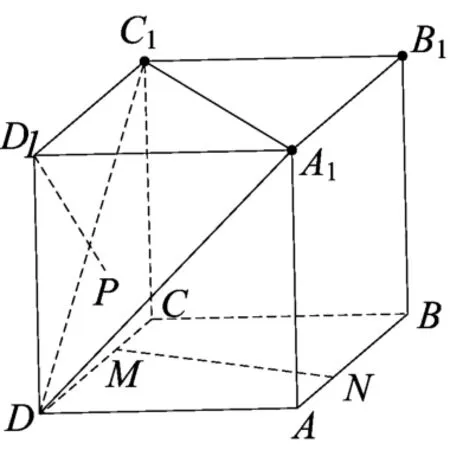
图7

例2(2017年金华十校4月模考)如图7,在正方体ABCD－A1B1C1D1中,点M,N分别是直线CD、AB上的动点,点P是△A1C1D内的动点(不包括边界),记直线D1P与MN所成角为θ,若θ的最小值为,试分析点P的轨迹．

解析根据直线与平面所成角的最小性可知:当直线MN是直线D1P在平面ABCD内的射影时,直线D1P与MN所成角θ最小,因此我们可知直线D1P与平面ABCD所成角为故直线D1P与直线D1D所成角为．因此点P在以D1D为轴、轴截面的顶角为的圆锥面上运动,又点P在△A1C1D内,且平面A1C1D与轴线D1D所成角为α且,因此点P的轨迹为椭圆的一部分．

2 理解助力问题求解的优化

对于定量化的动态立体几何问题,构建函数模型是解决问题非常重要的途径．函数模型的建构则需要基于一定的问题理解力,问题理解深浅程度则严重影响函数模型的优劣．

例3(2017年台州高三期末)如图8,在矩形ABCD中,AB＝4,BC＝6,四边形AEFG为边长为2的正方形．现将矩形ABCD沿过点F的动直线MN翻折,使翻折后的点C在平面AEFG上的射影C1落在直线AB上．若点C在折痕l上的射影为C2,求的最小值．

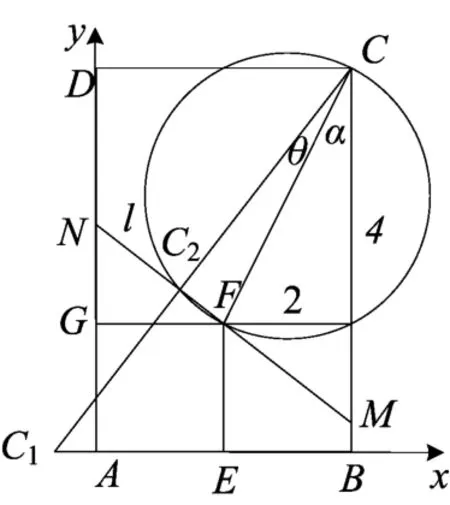
图8

解析按照我们对翻折问题的理解,我们作如下分析:如图9,设平面MCDN翻折后至平面MC′D′N．过点C作直线MN的垂线,垂足为C2,则在翻折过程中,点C在平面AEFG的射影在直线CC2上,从延长CC2交AB,此交点即为点C1．由此即为二面角C′－MN－A的平面角的余弦值．这样我们就将问题转化为如图8中的平面中的问题．考虑到该动态问题由直线MN的位置唯一确定,因此我们可以考虑建立直角坐标系,通过斜率来刻画MN的位置．

图9

建立以点A为坐标原点的直角坐标系,则C(4,6),从而PQ:y＝k(x－2)＋2(k＜0),则－kx＋y＋2k－2＝0,故由,可得点C1(6k＋4,0),则,从而故要使得取最小,则－k＋2＝ 5,故的最小值为3(2

根据不同的理解,我们还可以构建其他函数的模型．考虑到翻折前后与翻折线MN垂线的直线CC2C1特点:CC1⊥MN,则点C2在以CF为直径的圆上,因此本动态问题也可以由点C2的位置来确定．故要确定点C2的位置,我们可以设∠C2CF＝θ,为简便记∠FCB＝α,则．从而CC2＝FCcosθ＝25cosθ,CC1＝

显然不同的理解方式和理解深度对于函数模型的建构影响深远．

3 理解助力深入问题本源

立体几何的空间轨迹是近年来常考常新的热点．分析空间的轨迹常常会结合所求轨迹的特点,将我们熟悉的圆(特别是平面内到两定点的距离的比为非1的常数的动点轨迹为圆,此即阿波罗尼斯圆)和圆锥曲线的定义迁移至空间来直观求解．但是对于一些隐性的轨迹,我们还是需要在理解的基础上作图和分析．

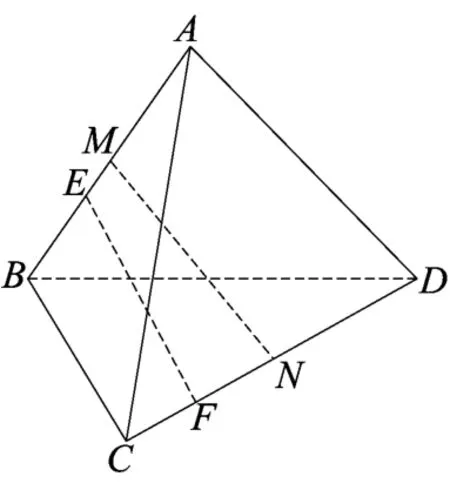
图10

例4(2017年台州4月模考)如图10,在棱长为2的正四面体A－BCD中,E、F分别为直线AB、CD上的动点,且 EF ＝．若记EF中点P的轨迹为L,求 L ．(注:L 表示L的测度,在本题L为曲线、平面图形、空间几何体时,L 分别对应长度、面积、体积．)

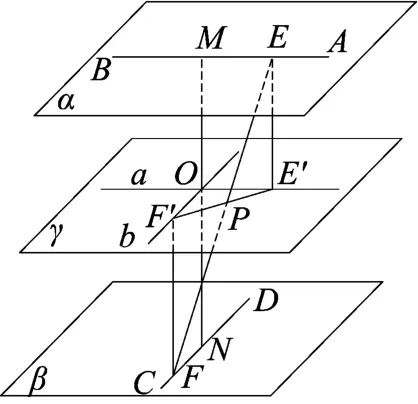
图11

解析从直观看,点P的轨迹应该在平行于AB、CD的“中位面”内．取线段AB、CD的中点M、N,则MN是异面直线AB、CD的公垂线．如图11,分别过AB、CD分别作垂直于公垂线MN的平面α、β,过MN的中点O作垂直于MN的垂面γ．在平面γ内分别过点O作平行于AB、CD的平行线a、b,设点E、F在平面γ内的射影分别为E′、F′．显然线段EF的中点P也为E′F′的中点,且点P在平面γ内．

在平面γ内,由于|E′F′|＝1,OE′⊥OF′,从而我们可知线段E′F′的中点P是以O为圆心,半径为的圆,从而点P的轨迹的长度为π．

至此我们已解决问题,但是在分析中我们发现AB、CD具有垂直关系,显然按照上述的理解,我们自然可以将问题转化为一般的情形,从而实现问题的一般化,

也即下面的问题:

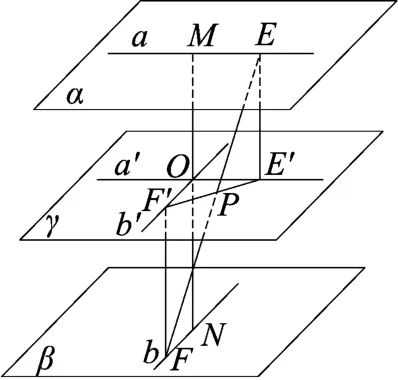
图12

例5如图12,已知MN为异面直线a、b的公垂线,且a、b之间的夹角为2θ,|MN|＝m．点E、F分别为a、b上的动点,且|EF|＝n．当点E,F运动时,求线段EF的中点P空间轨迹．

解析如图12,分别过点M、N及线段MN的中点O分别作垂直MN的平面α、β、γ,点E、F在平面γ的射影为E′、F′．则点P均是EF、E′F′的中点,且在平面γ内,并且|E′F′|＝,并设L＝

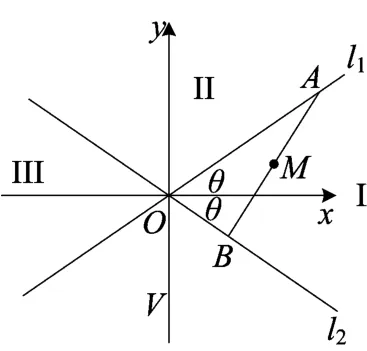
图13

在平面γ内过点O作直线a、b的平行线a′、b′,则a′、b′所成角为2θ．由此问题转化为平面γ内求点P的轨迹．如图13,在平面γ内,以O为坐标原点,以a′、b′所成角的角平分线作为x轴建立如图直角坐标系．

两条直线l1、l2把平面分成I、II、III、V 四个区域．由对称性,先设点当点P在区域I、III时．设|OA|＝s,|OB|＝t,则由余弦定理得s2＋t2－2stcos2θ＝L2．

设点A(x1,x1tanθ),B(x2,－x2tanθ),则s

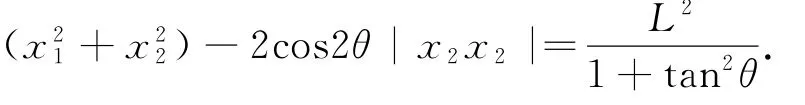
设点P(xP,yP),则

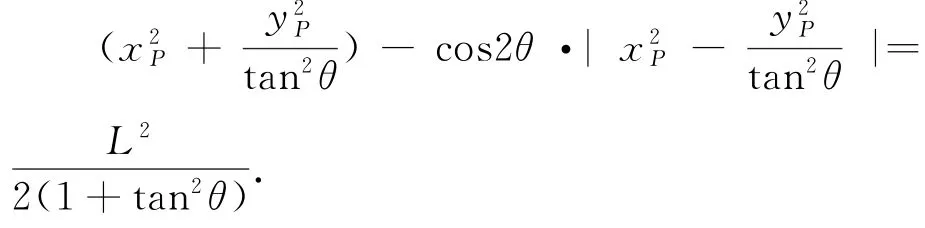
显然当l1⊥l2时,线段AB的中点P的轨迹方程为为圆的方程;当l1、l2不垂直时,线段AB的中点P的轨迹为椭圆．

图14

最后,我们利用上面的结果可快速解决问题:

例6已知正方体ABCD－A1B1C1D1的边长为2,点E、F分别在直线AB1、BC1上运动,且点P是线段EF的中点．若在空间中存在两点S、T,使得|PS|＋|PT|为定值,求该定值|PS|＋|PT|．

解析由于BC1//平面AB1D1,则异面直线AB1、BC1的公垂线段MN的长度|MN|即为点B到平面AB1D1的距离,也即为点A1到平面AB1D1的距离,故且AB,1BC1所成角为

结合图12,设点P的轨迹所在平面为平面γ,点E、F在平面γ内的射影分别为E′、F′．则|E′F′|＝ |EF|2－|MN|2＝2．由于异面直线AB1、BC1所成角为60°,则在平面γ内点P的轨迹方程为,即,从而根据椭圆的定义可知|PS|＋|PT|＝23．

尽管动态立体几何的问题千变万化,有在变化过程中分析空间元素的位置关系,有在变化中求解某个量的最值或范围,有在变换中分析某个点的轨迹等等．但是只要我们用心去理解问题,探寻解决问题的方法,反思和摸索问题解决的一般性策略,那么我们自然就提高了解决问题的效率,数学思维也会长足进步,才能在问题解决过程中享受数学无穷的乐趣．

1 林国夫．探析空间翻折问题的求解策略[J]．中学数学研究(广州)．2016年(11):42-45

2017-07-26)

本文系绍兴市规划课题《基于学生思维发展的高中数学选修课程的开发与实践》(立项序号SJG17270)阶段性成果．