代冬岩，朱桂英，李艳凤

（黑龙江八一农垦大学理学院，大庆 163319）

2+1维非线性KDV方程组的单行波解分类

代冬岩，朱桂英，李艳凤

（黑龙江八一农垦大学理学院，大庆 163319）

应用多项式的完全判别系统，以分类的形式给出2+1维非线性KDV方程组的单行波解，这个方法能够获得方程组的全部精确解，其中一部分是新解。同时通过赋予方程中参数具体数值，构造出单行波解的具体结构和波形图。

多项式完全判别系统；2+1维非线性KDV方程组；单行波解

KDV型方程是数学物理领域中的一个常见非线性模型，可用来描述很多实际物理现象。它是由Korteweg和Devries在1985年研究不能收缩且无黏滞液体表面机理时提出的[1]，KDV型方程在气体动力学、等离子体物理、流体力学等方面有重要的应用。近年来，国内外专家学者们开始关注于KDV型方程的求精确解研究，因为精确解可以清楚地分析非线性系统的变化规律，细致描述系统的本质特征，准确评估模型模拟的可靠性，因此，寻找非线性模型的精确解便成为非线性科学研究中的关键问题。由于非线性方程自身的特点，不同类型要运用不同的方法来求解，所以许多数学工作者致力于此方面的研究。Fan E[2]通过改进的齐次平衡法得到一系列耦合KDV方程的精确解，Li XZ[3]提出了一个扩展的F展开法找到了KDV方程的周期波解，Zhang DJ[4]运用Hirota法讨论出发生形变的KDV方程的N-孤立子解，Wazwaz[5]应用扩展的双曲正切法获得一些基于五阶非线性KDV方程形式的新的孤波解等，这些求解方法虽然能够求出方程的大量新解，但只能得到部分解。2004年刘提出一种求解方法—多项式完全判别系统法[6-7]，此法不仅简单直接，而且能够有效地给出方程精确解的全部分类，获得所有精确解，近些年有很多学者[8-10]应用这个方法求出大量非线性发展方程的精确解。

多项式完全判别系统方法的概述：先用行波变换把非线性发展方程组化为常微分方程组，再通过变量代入将其化简成只含一个因变量的常微分方程，形式如下：

此时u是因变量，θ1，θ2，…θs是参数，将方程（1）变为积分形式：F（u，θ1，θ2…，θs）是一个n阶的多项式，对应不同阶多项式的判别系统，通过积分法求出式（2）全部关于u的单行波解的分类。最后再根据相应关系式求出其他因变量的单行波解。

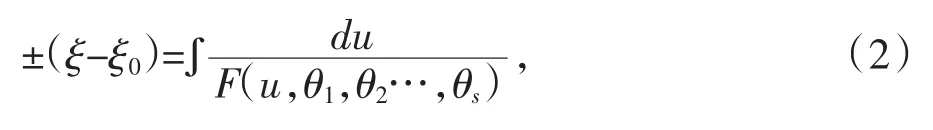
将利用三阶多项式的完全判别系统方法求解2+ 1维的非线性KDV方程组，以分类的形式求出2+1维非线性KDV方程组的所有单行波解，并且通过赋予参数具体数值，构造出单行波解的具体结构和波形图。

1 方程形式的转换

2+1维非线性KDV方程组：

首先，对方程（3）和（4）作单行波变换q=q（ξ），r=r（ξ），ξ=kx+ly+ωt，得到

再对方程（5）和（6）积分一次，得到

c1和c2为任意常数。

把式（9）代入方程（7）得到

对方程（10）再积分一次，形式如下

2 所有单行波解的分类

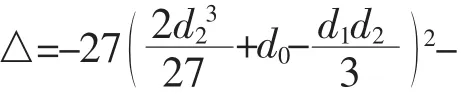
情况1：如果△=0，D1＜0，那么F（w）=（w-α）2（wβ），α≠β，原方程组q和r的解为

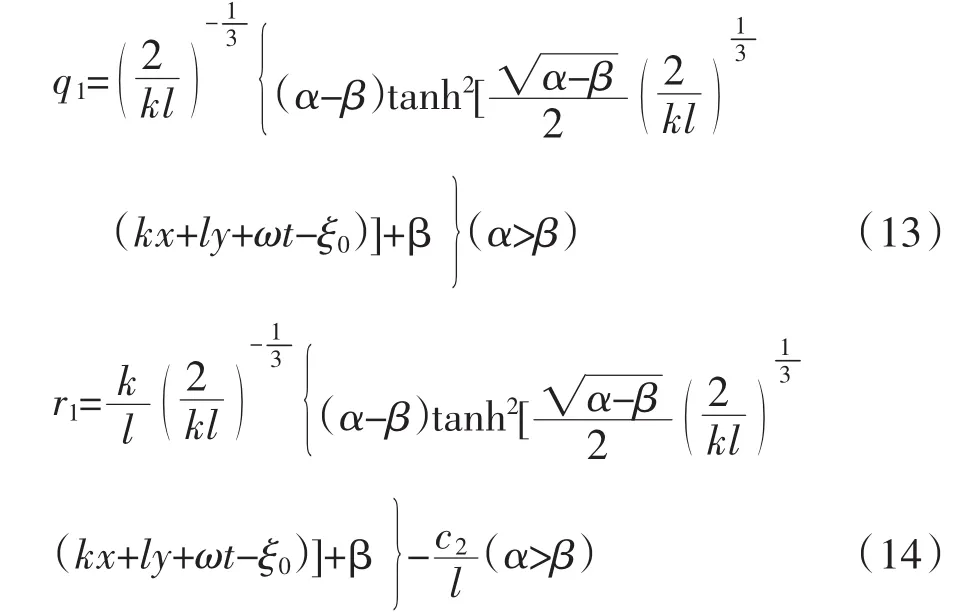
由于r的表达式可由q代入式（9）较容易求出，为了简便以下省略求r。

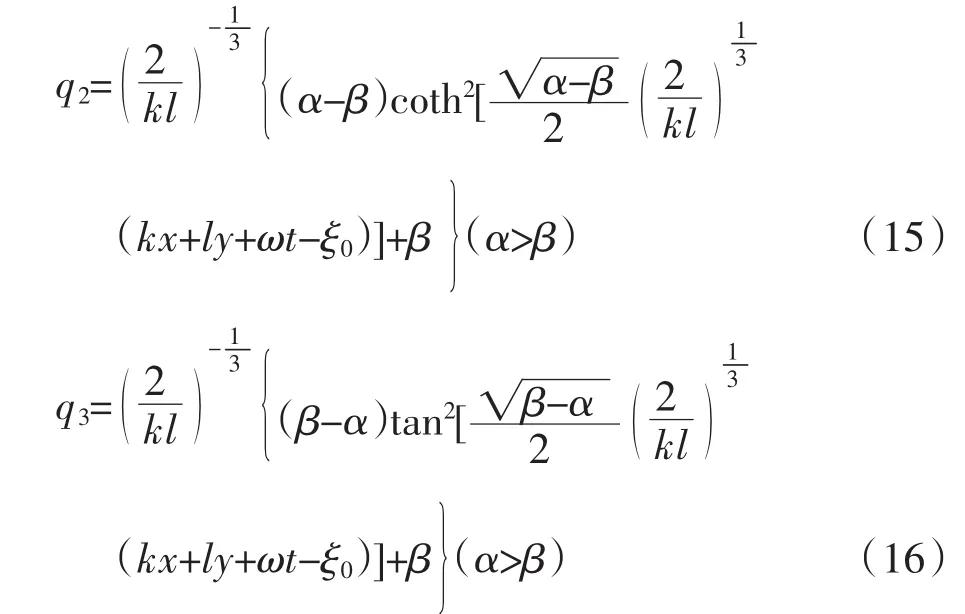
当α＞β，t=0时，参数值可取k=1，l=2，ω=1，c1= -，c2=0，得到α=1，β=-1，则式（13）和式（15）相应波形如图1和图2。当α＜β，t=0时，参数值可取k=1，l=2，ω=-1，c1=-，c2=0，得到α=-1，β=1，则式（16）相应的波形如图3。

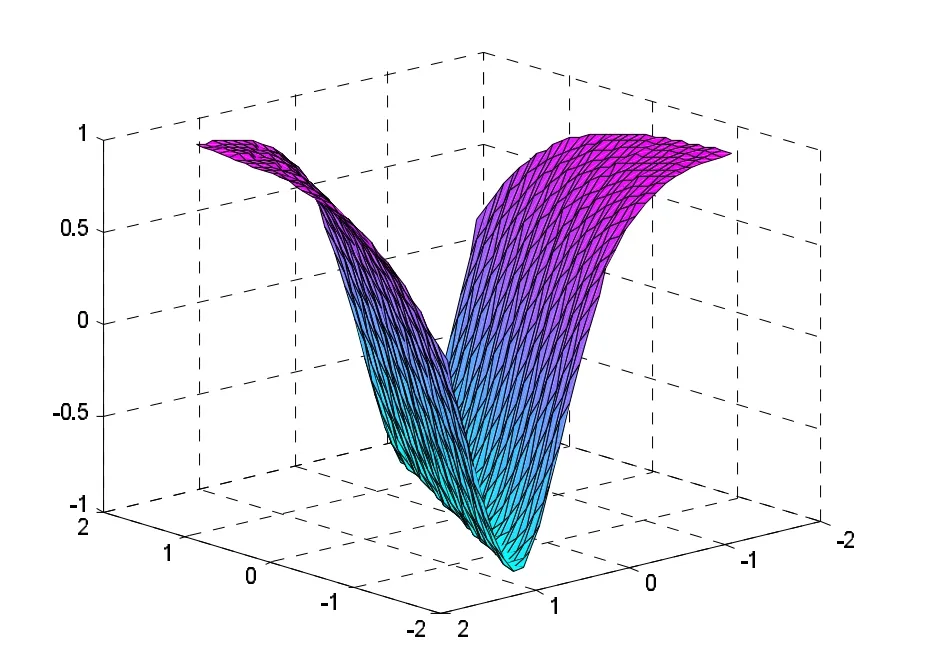
图1 钟形孤子解Fig.1Bell soliton solution

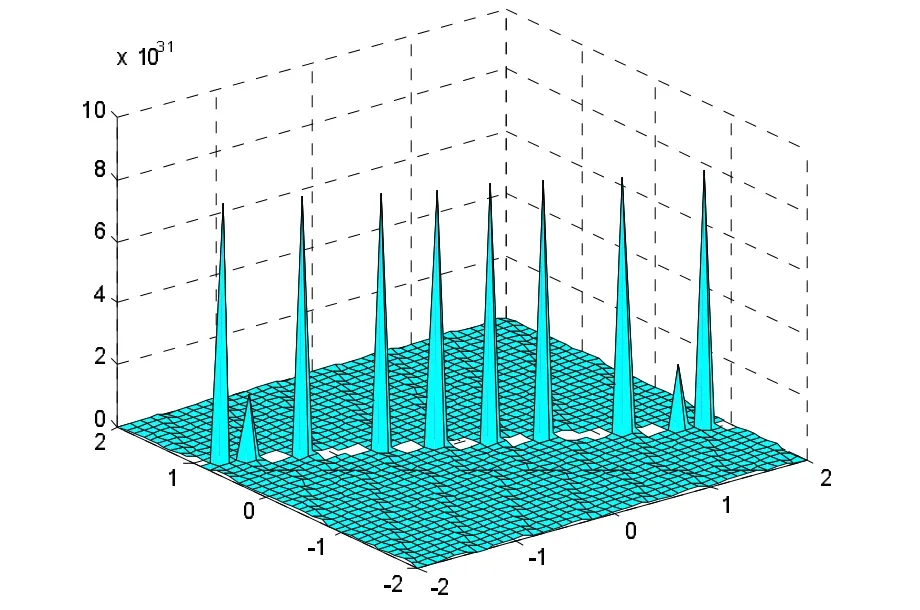
图2 多峰孤子解Fig.2Multimodal soliton solution

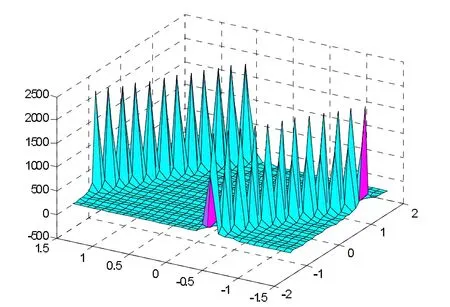
图3 周期解Fig.3Periodic solution

情况2：如果△=0，D1=0，那么F（w）=（w-α）3，原方程组q的解为

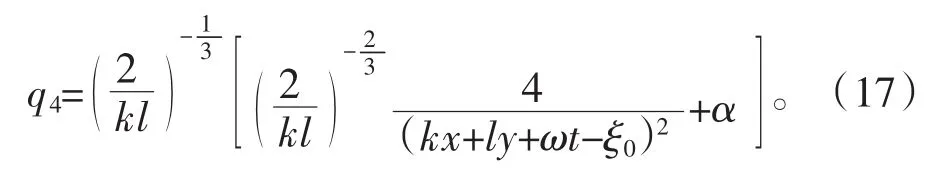
当t=0时，参数值可取k=1，l=2，ω=3，c1=，c2= 0，得到α=1，则式（17）相应的波形如图4。

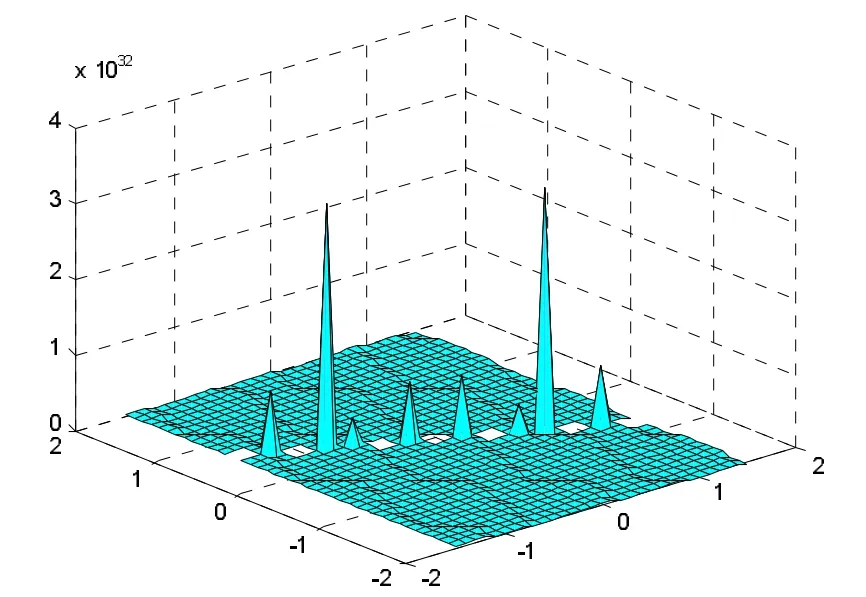
图4 有理式解Fig.4Rational expression solution

情况3：如果△＞0，D1＜0，那么F（w）=（w-α）（wβ）（w-γ）。假设α＜β＜γ，当α＜w＜β时，原方程组q的解为

情况3和4可用同样方法画出图像，这里不一一描述。

3 结论

对2+1维的非线性KDV方程组应用三阶多项式的完全判别系统方法来求解，可得到方程组全部精确解的分类，其中需要大量积分运算的数学技巧，以及借助合适的变量替换来简化计算过程，并且获得精确解的形式十分丰富，包括双曲周期解、有理函数解、孤波解和椭圆函数解等，其中一些还是新解。最后，通过赋予具体参数值构造出单行波解的波形图，这有利于进一步研究方程在物理等领域的应用[11]。

目前非线性发展方程的求解方法主要是一些方法的移置或推广，而多项式完全判别系统法并不是所有的方程都适用，所以对其适用范围还有待深入研究。

［1］Korteweg D J，Devries G.On the change of form of longwaves advancing in a rectangular canal and on a new type of long sationary waves［J］.Philosophical Magazine Series，1985，39（240）：422-443.

［2］Fan E，Zhang H.New exact solutions to a system of coupled KdV equations［J］.Physics Letters A，1998，245（5）：389-392.

［3］Li XZ，Wang ML，Li XY.Applications of F-expansion to Periodic Wave Solutions for KdV Equation［J］.Chaos Sol itons and Fractals，2005，24（5）：1257-1268.

［4］Zhang D J.The N-soliton solutions for the modified KdV equation with self-consistent sources［J］.Journal of the Physical Society of Japan，2002，71（71）：2649-2656.

［5］Wazwaz A M.The extended tanh method for new solitons solutions for many forms of the fifth-order KdV equations［J］.Applied Mathematics and Computation，2007，184（2）：1002-1014.

［6］Liu C S.Classification of All Single Travelling Wave Solutions to Calogero-Degasperis-Focas Equation［J］. CommunicationinTheoreticalPhysics，2007，48（10）：601-604.

［7］Liu C S.Solution of ODE u″+p（u）（u′）2+q（u）=0 and application Classifications of All Single Travelling wave Solutions to Some Nonlinear Mathematical Physics Equations［J］.Communication in Theoretical Physics，2008，49（2）：291-296.

［8］杜兴华.Maccari’s方程组新的精确行波解［J］.数学实践与认识，2010，40（13）：160-164.

［9］春玲，双叶.协同s-凸函数的Herimite-Hadamard型积分不等式［J］.内蒙古民族大学学报，自然科学版，2013，28（6）：627-630.

［10］Dai D Y，Yuan Y P.The classification and representation of single traveling wave solutions to the generalized Fornberg-Whitham equation［J］.Applied Mathematics and Computation，2014，242（8）：729-735.

［11］李欣.解非对称线性方程组的一种方法［J］.黑龙江八一农垦大学学报，2003，15（1）：93-96.

Classifying Single Traveling Wave Solution to the（2+1）-dimensional Nonlinear KDV Equations

Dai Dongyan，Zhu Guiying，Li Yanfeng
（School of Science，Heilongjiang Bayi Agriculture University，Daqing 163319）

By the complete discrimination system for polynomials，the classification of single traveling wave solutions were given for the（2+1）-dimensional nonlinear KDV equations.The method could obtain all the exact solutions to the equations and some of them were new.Under the concrete parameters，the single traveling wave figures of solutions were constructed.

complete discrimination system for polynomials；the（2+1）-dimensional nonlinear KDV system；single traveling wave solution

O175

A

1002-2090（2017）04-0133-04

10.3969/j.issn.1002-2090.2017.04.030

2017-03-17

黑龙江省大庆市科技计划指导项目（zd-2016-132）；黑龙江省大学生创新项目（201510223045）。

代冬岩（1980-），女，讲师，东北石油大学毕业，现主要从事数学物理方向的研究工作。