牛莉莉, 胡恒春

(上海理工大学 理学院,上海 200093)

非线性耦合Drinfeld-Sokolov-Satsuma-Hirota方程的对称约化

牛莉莉, 胡恒春

(上海理工大学 理学院,上海 200093)

由Clarkson和Kruskal提出的Clarkson-Kruskal直接法是一种不涉及群运算的求解非线性偏微分方程的代数方法,不同于经典李群方法,Clarkson-Kruskal直接法不需要求解复杂的初值问题.应用Clarkson-Kruskal直接法,并且利用相应规则得到非线性耦合Drinfeld-Sokolov-Satsuma-Hirota方程的对称约化.同时进一步求得了Drinfeld-Sokolov-Satsuma-Hirota方程新的相似变量和相似解,并与经典李群方法得到的结果进行对比,验证了Clarkson-Kruskal直接法与经典李群方法得到的结果可以互相变换.

对称约化; 非线性耦合Drinfeld-Sokolov-Satsuma-Hirota方程; Clarkson-Kruskal直接法

近年来,人们在不同科学领域中都发现和提出了用非线性方程来模拟不同的实验模型.因此,找到非线性发展方程的解具有非常重要的研究意义.如何求解非线性发展方程是一项困难的工作,经过数学家们和物理学家们多年的不懈努力,人们提出了许多有效的求解非线性发展方程的方法,如:Weierstrass椭圆函数展开法[1]、达布变换法[2]、Hirota双线性方法[3]、反散射方法[4]、李群方法[5-11]等.

本文研究Drinfeld-Sokolov-Satsuma-Hirota方程,简称DSSH方程,其形式如下:

(1)

该方程分别独立地由Drinfeld,Sokolov[12]和Satsuma,Hirota[13]提出.耦合DSSH方程是众多具有特殊形式Lax对的非线性方程之一,并且DSSH方程可以作为KP族的四约化的一个特殊情况,科学家们已经构建出它的精确单孤子解.Gürses和Karasu[14]发现了方程(1)的一个递归算子和一个双哈密顿结构,Wazwaz[15]用3种不同的方法,也就是Cole-Hopf变换、Hirota双线性方法和指数函数法,获得了其多孤子解、多个单孤子解以及平面周期解.下面采用Clarkson-Kruskal直接法(简称CK直接法)对方程(1)进行约化,并求出选取特殊常数后的新的相似解.

1 方法简介

众所周知,求解非线性系统的约化相似解,有3种常用方法:经典李群法、非经典李群法以及CK直接法.其中,经典及非经典李群法用到李群的思想,并且只能得到非线性偏微分方程的部分相似约化.

1989年,Clarkson和Kruskal提出将CK直接法应用于Boussinesq方程[16]和修正的Boussinesq方程[17],并得到了新的相似解,而用经典李群法和非经典李群法是得不到这些结果的.这种方法的主要优点是避免了复杂的群论分析,并且有时能够得到更多的相似约化结果.CK直接法被广泛应用在求解各种非线性偏微分方程上,如:对称正则长波方程[18]、修正的Benjamin-Bona-Mahoney 方程[18]等.

首先介绍相似变换的定义。

设u(x,t)是一个偏微分方程P(u)=0的解,作变换

(2)

使u′(x′,t′)也是偏微分方程P(u)=0的解,即

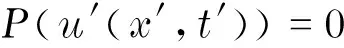
当式(2)为单参数李群变换时,可以得到从x,t,u(x,t)到x′,t′,u′(x′,t′)的不变变换条件

(3)

将式(2)代入到式(3)中可以确定ξ(x,t),τ(x,t),η(x,t),从而由式(3)的特征方程

确定出相似变量和相似变换.

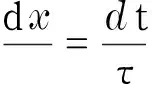
解得U(x,t,h(z,t),u)=c2,这时相似解可表示为

(4)

基于以上,可直接寻求形如式(4)的解.将式(4)代入到P(u)=0中,可得到ω(z)满足的一个常微分方程,这是偏微分方程的一个一般的相似约化[19].

CK直接法[16-22]的基本思想是:对一个偏微分方程

(5)

寻找一个如下形式的相似解

这是相似约化最一般的形式.将式(4)代入式(5)中,并且确保得到的结果是关于ω(z)的常微分方程,并且限制U和它的导数条件,使之能够解出U和ω的具体形式.

实际上,可以进一步假设方程(5)有如下形式的解

(6)

这里α(x,t),β(x,t),z(x,t)是关于x,t的待定函数.

将式(6)代入到方程(5)中,并且按ω(z)的幂次及其导数的阶数进行整理.为了使得到的结果是关于ω(z)的常微分方程,需要求ω(z)(或其导数)的不同幂次项的系数成比例,并且比值只能是z的函数.因此可得到关于α(x,t),β(x,t),z(x,t)的超定方程组,便可解得方程(5)的相似约化.

2 Drinfeld-Sokolov-Satsuma-Hirota方程的相似约化

对于DSSH方程,应用CK法求其对称约化、相似变量及相似解的步骤具体如下.

a. 可以容易证明,对于大部分方程都存在形式为u(x,t)=α(x,t)+β(x,t)ω(z(x,t))的相似约化,因此可假设方程(1)具有如下形式的对称变换

(7)

式中:α1,α2,β1,β2以及z(x,t)是关于x,t的待定函数;P(z),Q(z)是关于z的常微分方程.

b. 将式(7)代入式(1)中,将得到的结果按照P(z),Q(z)的幂次及其导数的阶数进行整理归纳得到

c. 找出其规范系数(假设为φ(x,t)),将P(z),Q(z)及其各阶导数的系数写成φ(x,t)Гi(z)的形式,其中Гi是z的待定函数.

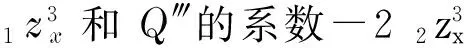
(10)

式中,Гi是关于z的待定函数.为计算方便,将经过一些运算后的Гi(z)仍记为Гi(z).

(11)

式中,Ωi是关于z的待定函数.

在接下来确定α1,α2,β1,β2和z时,在不失一般性,并且确保方法有效的前提下,对于DSSH方程,有以下5个自由度规则:

规则1 若α1(x,t)具有形式α1=α10(x,t)+β1(x,t)Ω(z(x,t)),那么取Ω(z)≡0(相当于作变换ω(z)→ω(z)-Ω(z));

规则2 若α2(x,t)具有形式α2=α20(x,t)+β2(x,t)Ω(z(x,t)),那么取Ω(z)≡0(相当于作变换ω(z)→ω(z)-Ω(z));

规则3 若β1(x,t)具有形式β1=β0(x,t).Ω(z(x,t)),那么取Ω(z)≡1(相当于作变换ω(z)→ω(z)/Ω(z));

规则4 若β2(x,t)具有形式β2=β0(x,t).Ω(z(x,t)),那么取Ω(z)≡1(相当于作变换ω(z)→ω(z)/Ω(z));

规则5 若z(x,t)是由方程Ω(z)=z0(x,t)确定的,那么取Ω(z)=z(相当于作变换z→Ω-1(z)).

接下来考虑zx的不同取值情况.

a. 当zx=0时,根据上述规则5可得,z是只关于t的函数,即z=t,因此P(z),Q(z)也是只关于t的函数,得到形式为一阶常微分方程的约化方程.因此重点考虑zx≠0的情况.

b. 根据上述5个规则,当zx≠0时,在方程(10)中由P‴和PP′前面的系数可知

(12)

进一步可得到

因此,利用规则3可知

(13)

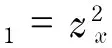
由规则5可知

再由规则5可得到z有如下形式

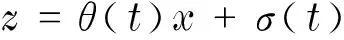
(14)

显然,再由式(13)可得

(15)

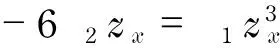
(16)

由上述规则2,便可得到

(17)

以及

(18)

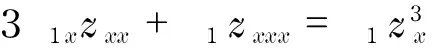
(19)

又因为z=θ(t)x+σ(t),方程(19)左边是关于x的线性函数,因此Г2有如下形式:

比较上述方程两边x的系数,可得

(20)

(21)

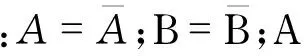
他们把这个消息报告李站长的时候，李站长虽然面上对放跑木材有些许恼怒，但当他看见卡车上粗壮奇秀的我时，顿时眉开眼笑，深谙当下苗木生意行情的他，心想这次搞到了一块肥肉，没收了就是公家的财物，实质上就是站里的财物，经过执法部门的拍卖就是合法的买卖，谁也说不起，看来上半年的创收任务有着落了。

因此,得到了非线性耦合DSSH方程的对称约化为

(22)

将上述方程(20)～(22)代入方程(1)中,可得

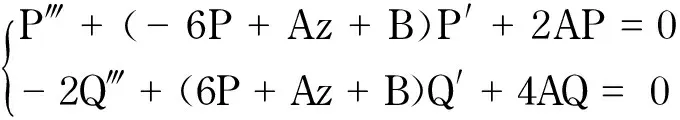
(23)

接下来考虑方程(23)的不同常数选取.

a. 当A=0时,可得到

式中,c1,c2是任意常数.

DSSH方程的对称约化为

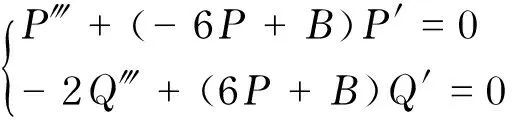
(24)

其中,P‴+(-6P+B)P′=0的解为椭圆积分,其形式为

(25)

式中,c1,c2是常数.

b. 当A≠0时,解方程(20)和(21),分别可得到

式中,c1,c2是常数.

DSSH方程的对称约化为

式中,P(z),Q(z)由方程(24)决定.

对以上CK直接法得到的相似约化作出适当的变换,便能够得到由经典李群变换导出的相似约化.在经典李群变换中,若Drinfeld-Sokolov-Satsuma-Hirota方程通过如下变换具有不变性,

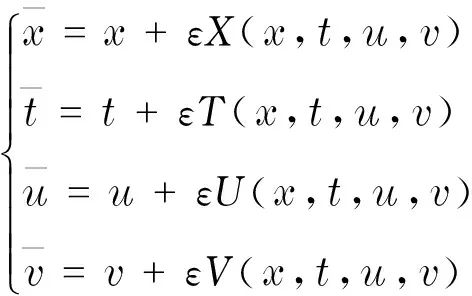
则群不变量z,P(z)以及Q(z)能够通过求解以下特征方程

得到.

在经典李对称中,群变换等价于

这里{σu,σv}是Drinfeld-Sokolov-Satsuma-Hirota方程对称方程的解

(26)

下面对应用CK直接法求得的式(22)进行群论的解释[23-24].

实际上,由已求得的式(14)可得到

即

同样的方法,由u=θ3P(z),v=θ4Q(z)可得到

即

因此,方程的对称约化具有如下形式:

(27)

若假设

即当A≠0时T=θ3,当A=0时T=1,式(27)求得的σ也是式(26)的解,也即由CK直接法求得的相似约化也可由经典李对称方法求得.

3 结论与展望

首先介绍了CK直接法求解偏微分方程的基本思想及具体步骤,并应用于Drinfeld-Sokolov-Satsuma-Hirota方程,得到了方程的对称约化以及其相似解.另外,比较了CK直接法和经典李群法的约化结果,可知CK直接法的结果可以推导出经典李群法的结果,即两种方法求得的结果可以互相变换.如何寻找其他类型的偏微分方程的约化结果也是今后的研究重点之一.

[1] CHEN Y,YAN Z Y.The Weierstrass elliptic function expansion method and its applications in nonlinear wave equations[J].Chaos,Solitons & Fractals,2006,29(4):948-964.

[2] MATVEEV V B,SALLE M A.Darboux transformations and solitons[M].Berlin:Springer,1991.

[3] HIROTA R.The direct method in soliton theory[M].Cambridge:Cambridge University Press,2004.

[4] ABLOWITZ M J,CLARKSON P A.Solitons,nonlinear evolution equations and inverse scattering[M].Cambridge:Cambridge University Press,1992.

[5] BLUMAN G W,KUMEI S.Symmetries and differential equations: applied mathematical sciences[M].New York:Springer,1989.

[6] OLVER P J.Applications of Lie groups to differential equations:graduate texts in mathematics[M].New York:Springer,1993.

[7] OVSIANNIKOV L V.Group analysis of differential equations[M].New York:Academic Press,1982.

[8] IBRAGIMOV N H.CRC handbook of Lie group analysis of differential equations,volume I[M].Boca Raton:CRC Press,1993.

[9] IBRAGIMOV N H.CRC handbook of Lie group analysis of differential equations, volume II[M].Boca Raton:CRC Press,1994.

[10] IBRAGIMOV N H.CRC handbook of Lie group analysis of differential equations, volume III[M].Boca Raton:CRC Press,1995.

[11] ADEM K R,KHALIQUE C M.Exact solutions and conservation laws of a (2+1)-dimensional nonlinear KP-BBM equation[J].Abstract and Applied Analysis,2013,2013:791863.

[12] DRINFELD V G,SOKOLOV V V.Equations of Korteweg-de Vries type and simple Lie algebras[J].DokladyAkademiiNauk SSSR, 1981,258:11-16.

[13] SATSUMA J,HIROTA R.A coupled KdV equation is one case of the four-reduction of the KP hierarchy[J].Journal of the Physical Society of Japan,1982,51(10):3390-3397.

[14] GÜRSES M,KARASU A.Integrable KdV systems: recursion operators of degree four[J].Physics Letters A,1999,251(4):247-249.

[15] WAZWAZ A M.The Cole-Hopf transformation and multiple soliton solutions for the integrable sixth-order Drinfeld-Sokolov-Satsuma-Hirota equation[J].Applied Mathematics and Computation,2009,207(1):248-255.

[16] CLARKSON P A,KRUSKAL M D.New similarity reductions of the Boussinesq equation[J].Journal of Mathematical Physics,1989,30(10):2201-2213.

[17] CLARKSON P A.New similarity solutions for the modified Boussinesq equation[J].Journal of Physics A:Mathematical and General,1989,22(13):2355-2367.

[18] CLARKSON P A.New similarity reductions and Painlevé analysis for the symmetric regularised long wave and modified Benjamin-Bona-Mahoney equations[J].Journal of Physics A:Mathematical and General,1989,22(18):3821-3848.

[19] CLARKSON P A,LUDLOW D K.Symmetry reductions,exact solutions,and Painlevé analysis for a generalized Boussinesq equation[J].Journal of Mathematical Analysis and Applications,1994,186(1):132-155.

[20] CLARKSON P A.Nonclassical symmetry reductions of the Boussinesq equation[J].Chaos,Solitons & Fractals,1995,5(12):2261-2301.

[21] CLARKSON P A,MANSFIELD E L,PRIESTLEY T J.Symmetries of a class of nonlinear third-order partial differential equations[J].Mathematical and Computer Modelling,1997,25(8/9):195-212.

[22] BLUMAN G W,COLE J D.Similarity methods for differential equations: applied mathematical sciences[M].New York:Springer,1974.

[23] MAN J.Similarity reductions and Painlevé property of coupled KdV equations[J].Communications in Theoretical Physics,2008,49(2):275-280.

[24] ADEM K R,KHALIQUEC M.On the solutions and conservation laws of the coupled Drinfeld-Sokolov-Satsuma-Hirotasystem[J].Boundary Value Problems,2014,2014:248.

(编辑:董 伟)

Symmetry Reduction for the Nonlinear Coupled Drinfeld-Sokolov-Satsuma-Hirota Equation

NIU Lili, HU Hengchun

(CollegeofScience,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)

The Clarkson-Kruskal direct method was proposed by Clarkson and Kruskal,which is an algebraic method for solving nonlinear partial differential equations.The advantage of this method is that it does not involve group theory operations and complex initial value problems.It can give new similarity solutions of the nonlinear evolution equations which could not be obtained by the classical Lie group method and the nonclassical Lie group method.By using the Clarkson-Kruskal method and corresponding rules,the symmetry reduction and the similarity transformation of the Drinfeld-Sokolov-Satsuma-Hirota equation were obtained.It is verified that the results by the Clarkson-Kruskal method can be transformed into those by the classical Lie group method.

symmetryreduction;nonlinearcoupledDrinfeld-Sokolov-Satsuma-Hirotaequation;Clarkson-Kruskaldirectmethod

1007-6735(2017)03-0205-05

10.13255/j.cnki.jusst.2017.03.001

2016-12-19

国家自然科学基金资助项目(11071164,11201302);上海市自然科学基金资助项目(10ZR1420800);上海市重点学科建设资助项目(XTKX2012)

牛莉莉(1993-),女,硕士研究生.研究方向:孤立子理论与可积系统.E-mail:546174910@qq.com

胡恒春(1976-),女,副教授.研究方向:孤立子理论与可积系统.E-mail:hhengchun@163.com

O 175

A