林 寿

(1. 闽南师范大学 数学与统计学院, 福建 漳州 363000; 2. 四川大学 数学科学学院, 四川 成都 610065)

《映射与空间》50年

林 寿1,2

(1. 闽南师范大学 数学与统计学院, 福建 漳州 363000; 2. 四川大学 数学科学学院, 四川 成都 610065)

1966年,著名的综述论文(A. V. Arhangel’skiǐ. Uspechi Mat Nauk,1966,21(4):133-184.)对一般拓扑学,尤其是广义度量空间理论,产生了强大的推动力.概述这50年间该文对一般拓扑学的历史意义与现实作用,列举了文中一些尚未解决的问题,同时介绍近年来Arhangel’skiǐ的工作对中国一般拓扑学发展的一些影响.

空间与映射的相互分类; 映射; 广义度量空间; 弱基;p空间; 拓扑代数

谨以本文纪念我国著名数学家、中国科学院院士、四川大学教授刘应明(1940—2016),深切缅怀刘应明老师为我国一般拓扑学及相关领域的发展与壮大所做出的卓越贡献.

广义度量空间理论是一般拓扑学的重要研究课题.关于广义度量空间理论的第一次系统和全面的综述报告当属D. K. Burke等[1]的文章.该文开篇就提到了广义度量空间理论的3个主要来源:度量化问题、积空间的仿紧性问题与Alexandroff设想.这一观点至今依然正确.

捷克斯洛伐克科学院与国际数学联盟于1961年在布拉格召开了第1届“一般拓扑学以及它与现代分析和代数的关系”的学术会议,简称布拉格拓扑学会议[2].在这次会议上,苏联科学院院士P. S. Alexandroff[3]做了关于拓扑空间及其连续映射的著名演讲,提出了用映射研究空间的设想,其核心内容是如下2类问题:

问题 1 什么空间类可以表为“好的”空间类(如度量空间类、零维空间类等)在“好的”连续映射下的像?

问题 2 什么空间类可以由“好的”映射类映入“好的”空间类?

Alexandroff问题是关于映射对空间进行分类的思想,导致了空间与映射相互分类的方法,其意义在于用映射作为工具提示各种拓扑空间类的内在规律,将映射作为纽带把五花八门的拓扑空间联结于一体.1966年A. V. Arhangel’skiǐ[4]发表了著名综述论文《映射与空间》,他认为:“空间与映射相互分类”的实质是下述3个密切联系的基本问题(这些问题在1978年P. S. Alexandroff等[5]论述点集拓扑学发展的几个奠基性时刻的综述报告中再次加以强调):

问题 3 在什么情况下,某个特定类A中的每个空间,在属于类F的映射作用下,能够被映成类B中的某个空间?

问题 4 如果F(A)是类A中的空间在属于类F的映射作用下的像空间全体,那么类F(A)中的空间具有怎样的内部特征?

问题 5 用F(A,B)表示一类映射,其定义域与值域分别是类A、类B中的空间,设H是另一映射类,则类F(A,B)∩H中的映射有哪些性质?

特别地,上述的一般提法包含了下述问题:

问题 6 在各类映射作用下,哪些拓扑性质保持不变?

《映射与空间》[4]开创了用映射研究空间的新纪元.它较系统地总结了一般拓扑学发展半个世纪来人们在映射理论方面所取得的重要成果,更重要的是对如何借助映射来研究各式各样的空间给出了一些具体的设想.50年的研究实践已表明[5-9]:这些设想不仅给一般拓扑学中许多经典的课题灌输了新鲜血液,而且产生了众多新的研究方向,带来了20世纪60年代末期至整个20世纪80年代一般拓扑学的繁荣景象,其中一些课题的持续探讨已发展成为21世纪初一般拓扑学中活跃的研究方向.

文献[4]提出了一些发展映射与空间理论的新概念,如弱基、弱第一可数性(文献[4]中定义2.3)、严格p空间(文献[4]中定义5.1)、σ仿紧空间(文献[4]中定义5.2)、伪乘积空间(文献[4]中定义5.3)、MOBI类(文献[4]中定义5.4)、MOBOS类(文献[4]中定义5.5)、FABOS类(文献[4]中定义5.6).本文试图以“核心问题”、“弱基”和“p空间”为切入点,从一个侧面说明关于空间与映射相互分类思想的来龙去脉以及它对激发新的研究工作的历史意义及现实作用.

本文依照文献[4]的约定,所有映射都是连续的满射,若未特别说明,所论的空间都是完全正则的空间.本文中τ表示实直线R的基数.

1 核心问题

《映射与空间》[4]分成6节,证明或引用定理43个,最重要的部分是所提出的问题,文中共引用、提出问题或猜想71个,其中33个给予标号的问题或猜想被作者认为是最困难的.首先从Arhangel’skiǐ问题[4]中选取6个已解决的问题给予论述.

问题 1.1(Alexandroff-Urysohn的问题[10]) 是否存在第一可数的Hausdorff的紧空间X使得|X|>τ?

问题 1.2(Ponomarev的问题) 完正规的Lindelöf空间是否是可分空间?

问题 1.3 闭映射把度量空间映成什么空间?

问题 1.4 如何刻画度量空间的商s映像?

问题 1.5 完备映射是否保持点可数基?

问题 1.6 具有点可数基的仿紧p空间是否是可度量化空间?

关于问题1.1[11]:“The work on the Problem gave a good push to developing and refining set-theoretic methods in General Topology.”文献[4]提出了下述相关问题:若第一可数的紧Hausdorff空间X是τ个度量子空间之并,则是否有|X|≤τ?1969年,A. V. Arhangel’skiǐ[12]证明了每一个Hausdorff的第一可数Lindelöf空间的基数都不超过τ,从而解决了问题1.1.而且与R. Hodel[13]开创了一般拓扑学的一个新的研究领域:拓扑空间上的基数函数.若用基数函数的语言,则Arhangel’skiǐ的定理可表述为:|X|≤2L(X)·χ(X),其中L(X)和χ(X)分别是拓扑空间X的Lindelöf数和特征.这一结果也成为A. V. Arhangel’skiǐ对于一般拓扑学的代表性贡献.

非可分的正则遗传Lindelöf空间称为L空间.问题1.2等价于著名的L空间问题:是否不存在L空间?关于问题1.2,A. V. Arhangel’skiǐ[4]提出了下述相关问题:具有点可数基的完正规的Lindelöf空间是否是可度量化空间?即是否不存在具有点可数基的L空间?现在基本上认为现代研究L空间与S空间(即非Lindelöf的正则遗传可分空间)的开篇之作是A. Jajnal等[14]于1968年发表的论文.L空间与S空间的探讨是集论拓扑的重要内容[6].如果不存在L空间,即问题1.2的回答是肯定的,则上述Arhangel’skiǐ的问题的回答也是肯定的.2006年,J. T. Moore[15]在ZFC中构造了第一个L空间,这也是对问题1.2的第一个完整的否定回答.2015年,Peng Y. H.[16]证明了J. T. Moore构造的L空间其平方不是一个Lindelöf空间.Peng Y. H.关于L空间的工作于2015年11月在闽南师范大学召开的“首届泛太平洋拓扑学及其应用国际会议”上获得了2015年度的Mary Ellen Rudin Young Researcher Award.至于是否存在具有点可数基的L空间,这是一个独立性问题.Z. Szentmikolóssy[17]证明了在假设MA+CH下不存在第一可数的L空间,F. D. Tall[18]在假设CH下构造了一个具有点可数基的L空间.

问题1.3和1.4是问题1和4的具体形式,其中问题1.3讨论的是“度量空间类”和“连续的闭映射类”,A. V. Arhangel’skiǐ[4]曾提到度量空间的闭映像是一个层空间;问题1.4讨论的是“度量空间类”和“商s映射类”.1966年,N. Lašnev[19]获得了度量空间的闭映像的第一个内在的刻画.现在把度量空间的闭映像称为Lašnev空间.1985年,L. Foged[20]利用k网给出了问题1.3一个较好的回答:拓扑空间X是一个度量空间的闭映像,当且仅当X是一个具有σ遗传闭包保持k网的正则的Fréchet-Urysohn空间,其中“遗传闭包保持集族”就是N. Lašnev[19]提出的概念.1987年,Y. Tanaka[21]利用cs*网也给出了问题1.4一个较好的回答:拓扑空间X是一个度量空间的商s映像当且仅当X是一个具有点可数cs*网的序列空间,这既表明了点可数集族的重要性,同时也显示了由Gao Z.[22]引入的cs*网的作用.

问题1.5相关于问题6讨论的是“完备映射类”和“点可数基性质”.1968年,V. V. Filippov[23]证明了完备映射保持具有点可数基的空间,肯定地回答了问题1.5.问题1.6既相关于问题2也联系于拓扑空间的度量化问题.1962年,A. S. Mišcenko[24]证明了具有点可数基的可数紧空间是可度量化空间;1963年,A. V. Arhangel’skiǐ[25]证明了仿紧p空间可刻画为度量空间的完备原像(更详细的叙述见本文第3节).1968年,V. V. Filippov[26]肯定地回答了问题1.6.问题1.4～1.6更引起了人们关注具有点可数覆盖空间的映射性质与度量化问题[27].

综上所述,上述所列的6个问题对于点集拓扑学未来发展的重要性至少体现在3个方面:一是开辟一般拓扑中新的研究领域;二是关注拓扑空间理论中的映射性质及度量化问题;三是探索及引导点可数覆盖的研究方向.

2 弱基

可对称空间产生于度量空间的商紧映像的研究[11].度量空间的商紧映像是可对称空间,但是未必是第一可数空间.A. V. Arhangel’skiǐ[4]引入了弱基及弱第一可数空间.

设集合X的每一点x对应X的含有点x的子集之族Tx,并且Tx关于有限交封闭.集族TC={Tx:x∈X}可按下述方式定义集合X上的拓扑T:子集P⊆X是闭的,当且仅当对于每一点x∈XP存在Q(x)∈Tx,使得Q(x)∩P=Ø.族TC称为拓扑T的弱基,Tx的元称为x的弱邻域.拓扑空间X称为满足弱第一可数性公理,简记gf可数性公理,如果X的拓扑可以由弱基TC={Tx:x∈X}给出,其中每一Tx是可数的.

上述集族Tx的来源就是对称空间(X,ρ)中的球形邻域族{Bρ(x,ε):ε>0},也可以看成是拓扑空间X中点x∈X的一种弱邻域基.弱基的引入开启了可对称空间的系统研究,并且指出了构建广义度量空间理论的新框架.R.E.Hodel[28]评论道:IwouldliketoemphasizethatArhangel’skiǐ’s1966paper“MappingsandSpaces”playedaveryimportantroleinthetheoryofsymmetrizablespaces.

第一可数空间等价于弱第一可数的Fréchet-Urysohn空间[4].每一对称空间是弱第一可数空间.每一弱第一可数空间是序列空间[29].A.V.Arhangel’skiǐ[4]给予弱基及对称空间极大的关注,提出的一些相关问题列举如下:

问题 2.1 满足gf可数公理的拓扑群是否是可度量化空间?

问题 2.2 具有点可数弱基的紧空间是否是可度量化空间?

问题 2.3 对称空间是否具有σ离散网?

问题 2.4 对称的仿紧空间是否是层空间?

问题 2.5MOBI类中的每个空间是否是对称空间?

问题 2.6 刻画度量空间的商紧映像?

问题 2.7 寻求可分度量空间的商紧映像的内在刻画.

N.V.Velicko[30]由弱邻域基出发引入弱展开的概念,给出对称空间以内在的刻画.F.Siwice[29]由弱基定义了几类重要的广义度量空间,如具有σ局部有限弱基的正则空间,发现了弱邻域具有“序列邻域”的性质,并证明了弱基可导出J.A.Guthrie[31]引入的cs网.在此基础上,林寿[32]和LiuC.等[33]分别引入了sn网和0弱基的概念.弱基是sn网和0弱基,sn网是cs网,0弱基和cs网都是cs*网.这些相关概念,形成了丰富的广义度量空间类[27],如g可度量空间、g可展空间、o可度量空间、sn可度量空间、cs-σ空间、sn对称空间、snf可数空间、0弱第一可数空间和csf可数空间等,对他们的研究已构成了广义度量空间理论的重要部分.

显然,问题2.1和2.2都涉及拓扑空间的度量化问题.

“Atypicalobjectoftopologicalalgebracanbedescribedasaresultofahappymarriageofanalgebraicstructurewithatopology.Thetiesarisingfromthismarriagestronglyinfluencethepropertiesofbothstructures.AclassicalexampleofthissituationisBirkhoff-KakutaniTheorem:atopologicalgroupGismetrizableifandonlyifitisfirst-countable”[11].

问题2.1来源于Birkhoff-Kakutani定理,这是A.V.Arhangel’skiǐ关于拓扑群的第一个问题,成为他后来系统研究拓扑代数的一个最早的标志.S.J.Nedev等[34]和P.J.Nyikos[35]都给出了问题2.1的肯定回答,由此导出拓扑代数中具有广义序列性质的研究[36-37].问题2.2是A.S.Mišcenko[24]关于点可数基的度量化定理情形的深化,T.Hoshina[38]肯定地回答了这个问题,由此激发由点可数覆盖所确定的紧空间,或可数紧空间,甚至伪紧空间的度量化问题的研究[27],如具有点可数k网的序列紧空间是可度量化空间[39];具有σ点有限基的伪紧空间是可度量化空间[40].

问题2.3和2.4及其解答中所涉及的概念“网”是拓扑空间中“基”概念的最重要、最成功的推广.A.V.Arhangel’skiǐ[41]为证明任意基数的Alexandroff-Urysohn加法定理时引进了“网”的概念.“网”既是A.V.Arhangel’skiǐ的处女之作,也是成名之作.J.Kofner[42]构造了不具有σ离散网的半度量空间,否定回答了问题2.3.这个问题的重要之处是表现了A.V.Arhangel’skiǐ[4]在研究了具有可数网空间性质的基础上[41],引入并关注具有σ离散网的空间,提出了一批涉及具有σ离散网空间的问题.除了问题2.3之外,还有如半度量的仿紧空间是否具有σ离散网?层空间是否具有σ离散网?1967年,A.Okuyama[43]把具有σ局部有限网的正则空间命名为σ空间.随后,F.Siwice等[44]证明了正则空间中具有σ离散网的空间等价于σ空间,也等价于具有σ闭包保持网的空间,从而使σ空间成为最具有代表性的广义度量空间[45].R.W.Heath[46]构造了一个具有可数网的正则的半度量空间,使它不是一个层空间,否定了问题2.4,并问保持仿紧的半度量空间是层空间的充要条件是什么?D.J.Lutzer[47]定义了k半层空间给上述Heath的问题予以肯定的回答.

问题2.5～2.7涉及度量空间的映像的研究.A.V.Arhangel’skiǐ[4]为研究问题1、3和4的一个富有特色的步骤是引入MOBI类.MOBI类是包含度量空间类且关于开紧映射封闭的最小的空间类.H.R.Bennett等[48]和M.M.Choban等[49]关于MOBI类的研究取得了重大进展.J.Chaber[50]构造了一个完全正则的弱仿紧的可展空间Z和一个开紧映射f:Z→X,使得X是完全正则空间,但X不是p空间(这概念在第3节中将重点论述),这时空间Z属于MOBI类,但是空间X不是对称空间,从而否定了问题2.5.问题2.6和2.7既与弱基相关又与问题1和4相关,同时也与MOBI类相关.N.N.Jakovlev[51]最早用点有限的弱展开序列刻画度量空间的商紧映像,回答了问题2.6.在正则空间类中,具有可数弱基的空间恰好刻画了可分度量空间的商紧映像[45],这给出问题2.7一个肯定的回答.2011年,T.V.An等[52]证明了一个Hausdorff空间X是一个度量空间的伪序列覆盖的紧映像当且仅当X具有点正则的cs*网.2012年,T.V.An等[53]又证明了一个Hausdorff空间X是一个可分度量空间的伪序列覆盖的紧映像,当且仅当X是具有可数cs*网的sn对称空间.如上所述,问题1.4及问题2.5～2.7等诱发了度量空间上关于紧覆盖映射及序列覆盖映射方面丰富多彩的工作,使其成为20世纪末以来空间与映射相互分类方法中最具活力的部分[27,54].

下面列举几个具有代表性的结果以说明对称空间及弱基的进一步作用.2013年,A.V.Arhangel’skiǐ[11]又重提了一些gf可数空间和对称空间的老问题,表明了他对这些内容的持续关注.

定理 2.8[55]对称空间是遗传的D空间.

定理 2.9[56]对称的1紧空间是遗传的Lindelöf空间.

定理 2.10[32]拓扑空间X具有点可数弱基当且仅当X是某一度量空间的1序列覆盖的商s映像.

定理 2.11 正则空间X具有σ离散弱基当且仅当X具有σ局部有限弱基[57],当且仅当X具有σ遗传闭包保持弱基[58].

定理 2.12[59-60]具有σ局部有限弱基的正则空间的正则的闭映像具有σ局部有限弱基当且仅当它是gf可数空间.

定理 2.13 拓扑空间X是可度量化空间,当且仅当存在空间X的覆盖列{Un},使得对于每一x∈X,{st2(x,Un):n∈N}是x在X中的弱邻域基[61],当且仅当X具有cs*正则弱基[27].

3 p空间

在问题1.6及问题2.5的解答中已提到了p空间.1963年,A. V. Arhangel’skiǐ[25]引进了p空间,并证明了拓扑空间X是一个度量空间的完备原像当且仅当X是一个仿紧的p空间,回答了P. S. Alexandroff提出的一个问题.是否每一p空间是可展空间的完备原像?为回答这一问题, A. V. Arhangel’skiǐ[4]引进了严格p空间.

完全正则空间X称为p空间[25],若存在X的极大紧化βX中开集族的序列{Un},满足:

1) Un覆盖X;

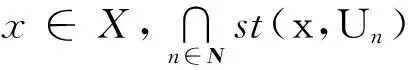
如果更设

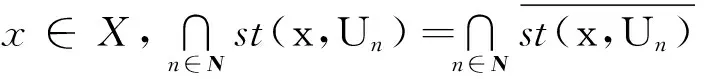
则X称为严格p空间[4].

可展空间的完备原像是严格p空间,但是p空间未必是严格p空间,如序空间ω1,所以p空间未必是可展空间的完备原像.严格p空间是否是可展空间的完备原像?为此,A. V. Arhangel’skiǐ[4]又引进了σ仿紧空间:拓扑空间X称为σ仿紧空间,若对于X的每一开覆盖U存在X的开覆盖列{Un}满足:对于每一x∈X存在m∈N和U∈U使得st(x,Um)⊆U.A.V.Arhangel’skiǐ[4]提出的一些与p空间及σ仿紧空间相关的问题,列举如下(它们主要涉及p空间,严格p空间及σ仿紧空间的内在刻画及映射定理):

问题 3.1 完备映射是否保持仿紧p空间性质?

问题 3.2 完备映射是否保持p空间性质?

问题 3.3 对称的或具有σ离散网的严格p空间是否是可展空间?

问题 3.4 σ仿紧空间的完备原像是σ仿紧空间?

问题 3.5 完备映射是否保持σ仿紧空间?

问题 3.6 具有σ离散网的空间是否是σ仿紧空间?

问题 3.7 弱仿紧,σ仿紧的p空间是仿紧空间?

问题 3.8 σ仿紧的p空间刻画了可展空间的完备原像?

问题 3.9MOBI类中的每个空间是否是p空间?p空间的开紧映像是否是p空间?

问题 3.10 度量空间的伪开紧映像是否是p空间?

问题3.1～3.3涉及p空间自身的性质.问题3.1最先由V.V.Filippov[62]给予肯定回答,即完备映射保持仿紧p空间性质.在第1节中的问题1.5和1.6的解答中已介绍过V.V.Filippov的贡献.1982年,J.Chaber[63]构造了一个σ仿Lindelöf的p空间使其任一完备映像不是一个p空间,从而否定地回答了问题3.2.J.Worrell[63-64]更早构造出完备映射不保持p空间的例子,但这例子一直没有发表.1969—1970年,D.K.Burke等[65-66]获得了后来广泛使用的严格p空间,p空间的内在刻画,并由此证明了可展空间类具有σ离散网的p空间类以及对称的p空间类是一致的[65],从而问题3.3的回答也是肯定的.

问题3.4～3.7涉及σ仿紧空间的等价刻画.D.K.Burke[67]引入了次仿紧空间:拓扑空间X称为次仿紧空间,若X的每一开覆盖具有σ离散的闭加细;并证明了σ仿紧性等价于次仿紧性,由此给出了问题3.4～3.6的肯定回答,甚至证明了闭映射保持σ仿紧空间.由于存在非仿紧的局部紧的弱仿紧、次仿紧空间[68],所以问题3.7的回答是否定的.在弱仿紧和次仿紧空间的基础上,刘应明[69]引入了拟仿紧空间和狭义拟仿紧空间,推广了Burke等的一些结果;并证明了在假设2>2下每一个可分正规的拟仿紧空间是仿紧的.这是我国学者关于集论拓扑学的第一个结果,所以刘应明是我国最先从事集论拓扑学研究的学者.

问题3.8～3.10涉及可展空间及p空间的映射性质.1971年,T.Isiwata[70]给出了可展空间的完备原像的一个内在刻画.J.Chaber[71]构造了一个局部紧的次仿紧空间,但它不可表为任一可展空间的完备原像,否定了问题3.8.J.Chaber[50]在否定上节问题2.5中所构造的例子也是对问题3.9的否定回答.V.J.Mancuso[72]证明了每一度量空间的伪开紧映像是一个可展空间,肯定回答了问题3.10.1976年,A.V.Arhangel’skiǐ[73]证明了每一度量空间的伪开紧映像刻画为弱仿紧的可展空间.

下面列举几个具有代表性的结果以说明p空间及σ仿紧空间的进一步作用.2011年,A.V.Arhangel’skiǐ等[74]又发表了关于p空间的论文,既表明了p空间强大的生命力,又展示了他们对于p空间的持续关注.

定理 3.11[67,75-76]对于拓扑空间X,下述条件相互等价:

1) X是σ仿紧空间;

2) X是次仿紧空间;

3) X的任一开覆盖具有σ局部有限的闭加细;

4) X的任一开覆盖具有σ闭包保持的闭加细;

5) X的任一开覆盖具有σ垫状加细.

定理 3.12 若X是一个p空间,则w(X)=nw(X)[77]且X具有可数型[78].

定理 3.13[79]设X是一个半拓扑群.若X是一个Baire,p空间,则X是一个仿拓扑群.

定理 3.14 拓扑空间X是严格p空间,当且仅当X是次亚紧的p空间[80],从而完备映射保持严格p空间性质.

定理 3.15[81]拓扑空间X是具有Gδ角线的p空间当且仅当X具有弱展开.

定理 3.16[82]拓扑空间X是可度量化空间,当且仅当X是具有Gδ对角线的单调正规的p空间.

4 尚未解决的问题

Arhangel’skiǐ[4]的论文共引用、提出问题或猜想71个,其中在ZFC中已解决的问题54个,已证明与ZFC相互独立的问题3个,尚未解决的问题还有14个.在尚未解决的14个问题中,在集论假设下相对解决的问题7个,尚无答案的问题7个.在前3节介绍了在ZFC中已解决的问题26个,与ZFC相互独立的问题1个.本节列出A.V.Arhangel’skiǐ[4]论文中尚未解决的14个问题,供读者进一步研究.

首先,列出在集论假设下相对解决的7个问题.

问题 4.1 在紧空间类中gf可数公理与第一可数公理是否等价?

N.N.Jakovlev[83]在假设CH下构造了一个紧Hausdorff的gf可数空间不具有点Gδ性质,否定了这问题.

问题 4.2 是否存在满足gf可数公理的紧空间X使得|X|>τ?

U.Abraham等[84]在假设κ=τ下肯定了这问题,并且在假设V[G]下构造了具有任意大基数的gf可数的紧空间.

问题 4.3 完正规紧空间的对称子空间是否是可度量化空间?

D.K.Burke等[85]在假设CH下构造了一个不可度量化的对称空间,使它有一个完正规的紧化,因而这问题在CH下是否定的.

问题 4.4 半度量的仿紧空间是否具有σ离散网?

E.S.Berney[86]在假设CH下构造了不具有σ离散网的正则遗传Lindelöf的半度量空间.

问题 4.5 正规的对称空间是否是仿紧空间?

W.G.Fleissner[87]在假设MA+CH下证明了Aronszajn树是一个不可度量化的正规Moore空间,于是这空间是非仿紧的正规的对称空间.

问题 4.6 在仿紧空间的每个闭映射下,原像不是紧集的点的全体的势是否不超过被映空间的权?

V.V.Filippov[88]在假设2>2下构造一个例子否定了这问题.

问题 4.7 具有可数基空间的商紧映像是否是层空间?

L.Foged[89]在假设MA下构造了一个非单调正规空间,使它是一个可分度量空间在有限到一商映射下的像,这例子表明这问题的回答是否定的.

其次,列出尚无答案的问题7个.

问题 4.8 集态正规的对称空间是否是仿紧空间?

问题 4.9 集态正规的对称空间是否可用连续一对一映射映成某一度量空间?

问题 4.10 完备映射是否保持MOBI类?

J.Chaber[90]证明了MOBI1类等价于具有点可数基的T1空间类,而完备映射保持具有点可数基的T1空间类[23],所以完备映射保持MOBI1类.

问题 4.11 正规空间是否是零维正规空间的不可约的完备映像?

问题 4.12 线段与线段的伪乘积是否具有可数基?

问题 4.13FABOC类中的空间具有怎样的内部特征?对于FABOC类中的空间,3种维数dim、ind和Ind是否相价?

FABOC类是包含可分度量空间类且关于商紧映射封闭的最小的空间类[4].显然,FABOC类中的空间都具有可数网.M.G.Charalambous[91]构造了一具有可数网的正则空间X使得dim(X)=1,ind(X)=2.

问题 4.14 完正规的Lindelöf空间是完正规k空间的连续映像?

5 A. V. Arhangel’skiǐ在中国

Alexandroff设想是广义度量空间理论的3个重要来源之一.《映射与空间》[4]系统地发展了P.S.Alexandroff的思想.前3节所介绍的A.V.Arhangel’skiǐ的问题对于数理逻辑和集论拓扑、映射理论、广义度量空间理论和覆盖性质等一般拓扑学及相关的重要课题的研究产生了强有力的推动作用[92-93].

《映射与空间》[4]由苏州大学吴利生、陈必胜翻译成中文,于1981—1982年在《数学译林》分3期刊出.1983年上海光华出版社出版由刘应明、高国士等编辑的论文集《SelectedPapersonTopologyI,II,III》,选取从1937—1979年国际上较有影响的一般拓扑学论文115篇[94],其中收入了《映射与空间》[4](俄文).A.V.Arhangel’skiǐ的著作《FundamentalsofGeneralTopology:ProblemsandExercises》[95]和《GeneralTopologyI》[96]曾在中国印刷发行.在20世纪70年代末到80年代这个中国历史上独特的时期中,这些珍贵的资料对于推动我国一般拓扑学的复苏及其后续的发展起到了较大的作用[97-98],如高国士[99]在《拓扑空间论》的序言中就很自豪地写道:本书是《映射与空间》理论的发展与应用.

A.V.Arhangel’skiǐ曾3次到中国访问,其中2006年11月27日—12月7日到首都师范大学和漳州师范学院访问;2012年9月22日—10月1日到南京参加“拓扑学及其相关领域国际会议”,做了题为“Somepropertiesofremaindersofmetrizableandclosetothemspaces”的40min大会邀请报告,并到南京大学、南京师范大学和苏州大学访问;2015年11月25日—12月8日到漳州参加“首届泛太平洋拓扑学及其应用国际会议”,并到闽南师范大学访问.

A.V.Arhangel’skiǐ的研究工作涉及与一般拓扑学及其应用相关的广泛领域,如空间与映射的相互分类、度量空间及其推广、紧性及其推广、拓扑空间的基数函数、连续函数空间理论、拓扑群、拓扑代数和拓扑空间的齐性等.在过去的近60年间,A.V.Arhangel’skiǐ所引进的新概念、获得的新结果和提出的大量问题成为一般拓扑学向前推进的巨大动力,深深地影响着当代一般拓扑学的前进方向.近年来,A.V.Arhangel’skiǐ及其部分学生(如M.M.Choban、M.G.Tkachenko、V.G.Pestov、I.I.Guran、V.V.Uspenskij、D.B.Shakhmatov、O.G.Okunev、O.V.Sipacheva、E.A.Reznichenko、A.S.Gul’ko、C.Liu)的研究兴趣主要在拓扑代数方面[36].从空间与映射的相互分类,到连续函数空间,到拓扑群,到拓扑代数及拓扑空间的齐性等,其研究方向的变化轨迹本身就是一道优美的弧线.

1925年O.Schreier[100]和1927年F.Leja[101]分别独立地给出了第一个Hausdorff拓扑群的现代定义.我国老一辈拓扑学家胡世桢[102]在20世纪40年代曾在一致空间及齐性空间方面做过工作.20世纪50年代,苏联科学院院士庞特里亚金[103-104]的著作《连续群》被译成中文.中国科学院院士关肇直[105]早年的著作《拓扑空间概论》中也有关于拓扑群的介绍.黎景辉等[106]的《拓扑群引论》作为《现代数学基础丛书》之38辑在科学出版社出版.这些均未对国内关于拓扑群的研究工作产生重要的影响.作为一个较成熟的研究课题,在国内拓扑群理论似乎只作为代数、分析等学科的基础知识而存在.自从A.V.Arhangel’skiǐ等到中国不遗余力地弘扬拓扑代数之后,情况发生了显著的变化.从2009年起,国内的青年学者开始发表拓扑代数的论文[107],而后逐渐在国际舞台上崭露头脚,继而出现了拓扑代数的研究群体,如2014—2015年我国学者在《TopologyanditsApplications》上发表的拓扑代数方面的论文有19篇,解决了若干包括A.V.Arhangel’skiǐ在内的拓扑代数名家提出的问题,获得了国际同行的认可与高度评价.A.V.Arhangel’skiǐ的中国之旅及其著作对推动我国拓扑代数水平的迅速提升并进入国际研究前沿发挥了巨大的作用[37,108-109].

[1] BURKE D K, LUTZER D J. Recent advances in the theory of generalized metric spaces[C]//Lecture Notes in Pure and Applied Mathematics, 24. New York:Marcel Dekker,1976:1-70.

[2] Czechoslovak Academy of Sciences. General topology and its relations to modern analysis and algebra I[C]//Proc 1st Topological Symp. New York:Academic Press,1962:5.

[3] ALEXANDROFF P S. On some results concerning topological spaces and their continuous mappings[C]//General Topology and its Relations to Modern Analysis and Algebra I. Proc 1st Topological Symp. New York:Academic Press,1962:41-54.

[4] ARHANGEL’SKII A V. Mappings and spaces[J]. Uspechi Mat Nauk,1966,21(4):133-184.

[5] ALEXANDROFF P S, FEDORCHUK V V, ZAICEV V I. The main aspects in the development of set-theoretic topology[J]. Uspechi Mat Nauk,1978,33(3):3-48.

[6] KUNEN K, VAUGHAN J E. Handbook of Set-theoretic Topology[M]. Amsterdam:Elsevier Science Publishers,1984.

[7] HUSEK M, VAN MILL J. Recent Progress in General Topology[M]. Amsterdam:Elsevier Science Publishers,1992.

[8] HUSEK M, VAN MILL J. Recent Progress in General Topology II[M]. Amsterdam:Elsevier Science Publishers,2002.

[9] HART K P, VAN MILL J, SIMON P. Recent Progress in General Topology III[M]. Pairs:Atlantis Press,2014.

[10] ALEXANDROFF P S, URYSOHN P S. Mémoire sur les espaces topologiques compacts[J]. Verh Koninkl Akad Wetensch,1929,14:1-96.

[11] ARHANGEL’SKII A V. Selected old open problems in general topology[J]. Bil Acad Stiinte Repub Mold Mat,2013,72(2):37-46.

[12] ARHANGEL’SKII A V. The cardinality of first-countable bicompacta[J]. Dokl Akad Nauk SSSR,1969,187:967-970.

[13] HODEL R. Cardinal functions I[C]//KUNEN K, VAUGHAN J E. Handbook of Set-theoretic Topology. Amsterdam:Elsevier Science Publishers,1984:1-61.

[14] JAJNAL A, JUHASZ I. On hereditarilyα-Lindelöf and hereditarilyα-separable spaces[J]. Ann Univ Sci Budapest,1968,9:115-124.

[15] MOORE J T. A solution to the L space problem[J]. J Am Math Soc,2006,19(3):717-736.

[16] PENG Y H. AnLspace with non-Lindelöf square[J]. Topology Proc,2015,46:233-242.

[17] SZENTMIKOLOSSY Z.S-spaces andL-spaces under Martin’s Axiom[J]. Colloq Math Soc Janos Bolyai,1978,23:1139-1145.

[18] TALL F D. On the existence of normal metacompact Moore spaces which are not metrizable[J]. Canad J Math,1974,26:1-6.

[19] LASNEV N. Closed images of metric spaces[J]. Dokl Akad Nauk SSSR,1966,170:505-507.

[20] FOGED L. A characterization of closed images of metric spaces[J]. Proc Am Math Soc,1985,95:487-490.

[21] TANAKA Y. Point-countable covers andk-networks[J]. Topology Proc,1987,12:327-349.

[23] FILIPPOV V V. Preservation of the order of a base under a perfect mapping[J]. Dokl Akad Nauk SSSR,1968,181:1077-1079.

[24] MISCENKO A S. Spaces with a pointwise denumerable basis[J]. Dokl Akad Nauk SSSR,1962,144:985-988.

[25] ARHANGEL’SKII A V. On a class of spaces containing all metric and all locally bicompact spaces[J]. Dokl Akad Nauk SSSR,1963,151:751-754.

[26] FILIPPOV V V. On feathered paracompacta[J]. Dokl Akad Nauk SSSR,1968,178(3):555-558.

[27] 林寿. 点可数覆盖与序列覆盖映射[M]. 2 版. 北京:科学出版社,2015.

[28] HODEL R E. A history of generalized metrizable spaces[C]//AULL C E, LOWEN R. Handbook of the History of General Topology. 2nd ed. Dordrecht:Kluwer Academic Publishers,1998,541-576.

[29] SIWICE F. On defining a space by a weak base[J]. Pacific J Math,1974,52:233-245.

[30] VELICKO N V. Symmetrizable spaces[J]. Mat Zametki,1972,12(5):577-582.

[31] GUTHRIE J A. A characterization of0-spaces[J]. General Topology Appl,1971,1:105-110.

[32] 林寿. 关于序列覆盖s映射[J]. 数学进展,1996,25:548-551.

[33] LIU C, LIN S. On countable-to-one maps[J]. Topology Appl,2007,154:449-454.

[34] NEDEV S J, CHOBAN M M. On metrization of topological groups[J]. Vestnik Moskow Univ Mat Meh,1968,6:18-20.

[35] NYIKOS P J. Metrizability and the Fréchet-Urysohn property in topological groups[J]. Proc Am Math Soc,1981,83:793-801.

[36] ARHANGEL’SKII A V, TKACHENKO M. Topological Groups and Related Structures[M]. Paris:Atlantis Press and World Sci,2008.

[37] 林福财. 拓扑代数与广义度量空间[M]. 厦门:厦门大学出版社,2012.

[38] HOSHINA T. On the quotients-images of metric spaces[J]. Sci Rep Tokyo Kyoiku Daigaku Sect A,1970,10:265-268.

[39] CAI Z Y, LIN S. Sequentially compact spaces with a point-countablek-network[J]. Topology Appl,2015,193:162-166.

[40] USPENSKIJ V V. Pseudocompact spaces with aσ-point-finite base are metrizable[J]. Comment Math Univ Carolinae,1984,25:261-264.

[41] ARHANGEL’SKII A V. An addition theorem for the weight of sets lying in bicompacts[J]. Dokl Akad Nauk SSSR,1959,126(2):239-241.

[42] KOFNER J. On a new class of spaces and some problems of symmetrizable theory[J]. Dokl Akad Nauk SSSR,1969,187(2):270-273.

[43] OKUYAMA A. Some generalizations of metric spaces, their metrization theorems and product spaces[J]. Sci Rep Tokyo Kyioku Daigaku Sect A,1967,9:236-254.

[44] SIWICE F, NAGATA J. A note on nets and metrization[J]. Proc Jpn Acad,1968,44:623-727.

[45] 林寿. 广义度量空间与映射[M]. 2 版. 北京:科学出版社,2007.

[46] HEATH R W. A paracompact semi-metric space which is not anM3-space[J]. Proc Am Math Soc,1966,17:868-870.

[47] LUTZER D J. Semimetrizable and stratifiable spaces[J]. General Topology Appl,1971,1:43-48.

[48] BENNETT H R, CHABER J. A survey of the class MOBI[C]//VAN MILL J, REED G M. Open Problems in Topology. Amsterdam:North-Holland,1990:221-229.

[49] CHOBAN M M. The open mappings and spaces[J]. Ren Circolo Math Palermo,1992,29(1):51-104.

[50] CHABER J. Metacompactness and the class MOBI[J]. Fund Math,1976,91:211-217.

[51] JAKOVLEV N N. Ong-metrizable spaces[J]. Dokl Akad Nauk SSSR,1976,226(3):530-532.

[52] AN T V, TUYEN L Q. On an affirmative answer to S. Lin’s problem[J]. Topology Appl,2011,158:1567-1570.

[53] AN T V, TUYEN L Q. Onπ-images of separable metric spaces and a problem of Shou Lin[J]. Mat Vesnik,2012,64(4):297-302.

[54] MICHAEL E A. Some problems[C]//VAN MILL J, REED G M. Open Problems in Topology. Amsterdam:North-Holland,1990:271-278.

[55] BURKE D K. Weak-bases andD-spaces[J]. Comment Math Univ Carolinae,2007,48(2):281-289.

[56] NEDEV S J. Symmetrizable spaces and final compactness[J]. Dokl Akad Nauk SSSR,1967,175:532-534.

[57] FOGED L. Ong-metrizability[J]. Pacific J Math,1982,98:327-332.

[58] LIU C. On weak bases[J]. Topology Appl,2005,150:91-99.

[59] 林寿. 关于g-可度量空间[J]. 数学年刊,1992,A13(3):403-409.

[60] TANAKA Y.σ-hereditarily closure-preservingk-networks andg-metrizability[J]. Proc Am Math Soc,1991,112:283-290.

[61] MARTIN H W. Weak bases and metrization[J]. Trans Am Math Soc,1976,222:337-344.

[62] FILIPPOV V V. The perfect image of a paracompact feathered space[J]. Dokl Akad Nauk SSSR,1967,176(3):533-535.

[63] CHABER J. Perfect images ofp-spaces[J]. Proc Am Math Soc,1982,85:609-614.

[64] ARHANGEL’SKII A V. Notes on the history of general topology in Russia[J]. Topology Proc,2000,25:353-395.

[65] BURKE D K, STOLTENBERG R A. A note onp-spaces and Moore spaces[J]. Pacific J Math,1969,30:601-608.

[66] BURKE D K. Onp-spaces andwΔ-spaces[J]. Pacific J Math,1970,35:285-296.

[67] BURKE D K. On subparacompact spaces[J]. Proc Am Math Soc,1969,23:655-663.

[68] BURKE D K. Covering properties[C]//KUNEN K, VAUGHAN J E. Handbook of Set-theoretic Topology. Amsterdam:Elsevier Science Publishers,1984:347-422.

[69] 刘应明. 一类包含弱仿紧空间和次仿紧空间的拓扑空间[J]. 数学学报,1977,20:212-214.

[70] ISIWATA T. Inverse images of developable spaces[J]. Bull Tokyo Gakugei Univ Math Sci,1971,23:11-21.

[71] CHABER J. Perfect preimages of Moore spaces[J]. Bull Acad Pol Sci:Math,1983,31:31-34.

[72] MANCUSO V J. Inverse images and first countability[J]. General Topology Appl,1972,2:29-44.

[73] ARHANGEL’SKII A V. Intersection of topologies, and pseudo-open bicompact mappings[J]. Dokl Akad Nauk SSSR,1976,226(4):745-748.

[74] ARHANGEL’SKII A V, CHOBAN M M. Some generalizations of the concept of ap-space[J]. Topology Appl,2011,158(2):1381-1389.

[75] CHOBAN M M. Onσ-paracompact spaces[J]. Vestnik Moskow Univ Mat Mech,1969,22:20-27.

[76] JUNNILA H J K. On submetacompactness[J]. Topology Proc,1978,3:375-405.

[77] ARHANGEL’SKII A V. Bicompact sets and the topology of spaces[J]. Trudy Moskow Mat Obsch,1965,13:3-55.

[78] CHOBAN M. Perfect mappings and spaces of countable type[J]. Vestnik Moskow Univ:Mat Mech,1967,22(6):87-96.

[79] BOUZIAD A. Continuity of separately continuous group actions onp-spaces[J]. Topology Appl,1996,71:119-124.

[80] JIANG S. Every strictp-space isθ-refinable[J]. Topology Proc,1986,11:309-316.

[81] ALLECHE B, ARHANGEL’SKII A V, CALBRIX J. Weak developments and metrization[J]. Topology Appl,2000,100:23-38.

[82] HEATH R W, LUTZER D J, ZENOR P L. Monotonically normal spaces[J]. Trans Am Math Soc,1973,178:481-493.

[83] JAKOVLEV N N. On the theory ofo-metrizable spaces[J]. Dokl Akad Nauk SSSR,1976,229(6):1330-1331.

[84] ABRAHAM U, GORELIC I, JUHASZ I. On Jakovlev spaces[J]. Isr J Math,2006,152:205-219.

[85] BURKE D K, DAVIS S W. Compactifications of symmetrizable spaces[J]. Proc Am Math Soc,1981,81:647-651.

[86] BERNEY E S. A regular Lindelöf semi-metric space which has no countable network[J]. Proc Am Math Soc,1970,26:361-364.

[87] FLEISSNER W G. When is Jones’ space normal?[J]. Proc Am Math Soc,1975,50:375-378.

[88] FILIPPOV V V. On the “degree of non-bicompactness” of a closed mapping of a paracompacta[J]. Vestnik Moskow Univ:Mat Mech,1972,27(4):9-11.

[89] FOGED L. Normality ink-and-spaces[J]. Topology Appl,1986,22:223-240.

[90] CHABER J. On the class MOBI[C]//FROLIC Z. Proc 6th Prague Topological Symp. General Topology and its Relations to Modern Analysis and Algebra VI. Berlin:Heldermann Verlag,1988:77-82.

[91] CHARALAMBOUS M G. Resolving a question of Arkhangel’skiǐ’s[J]. Fund Math,2006,192:67-76.

[92] 林寿. 关于ARHANGEL’SKII的《映射与空间》[J]. 苏州大学学报(自然科学版),1992,8(4):393-400.

[93] 林寿. 关于ARHANGEL’SKII的《映射与空间》(续)[J]. 苏州大学学报(自然科学版),1993,9(1):11-19.

[94] 程民德. 中国现代数学家传:第3卷[M]. 南京:江苏教育出版社,1998:292.

[95] ARHANGEL’SKII A V, PONOMAREV V I. Fundamentals of general topology:problems and exercises[C]//JAIN V K. Mathematics and its Applications, 13. Dordrecht:Kluwer Academic Publishers,1984.

[96] ARHANGEL’SKII A V, PONTRYAGIN L S. General topology I[C]//Encyclopaedia of Mathematical Sciences, 17. Berlin:Springer-Verlag,1990.

[97] 刘应明. 拓扑学(一般拓扑学)[C]//自然科学年鉴. 北京：科学出版社,1982.

[98] 刘应明,蒋继光. 点集拓扑学[C]//自然科学年鉴. 北京：科学出版社,1989.

[99] 高国士. 拓扑空间论[M]. 北京:科学出版社,2000.

[100] SCHREIER O. Abstrakte kontinuerliche Gruppen[J]. Abh Math Sem Univ Hamburg,1925,4:15-32.

[101] LEJA F. Sur la notion du group abstrait topologique[J]. Fund Math,1927,9:37-44.

[102] 陈克胜. 民国时期中国拓扑学史稿[M]. 北京:科学出版社,2014.

[103] 庞特里亚金. 连续群(上册)[M]. 曹锡华,译. 北京:科学出版社,1957.

[104] 庞特里亚金. 连续群(下册)[M]. 曹锡华,译. 北京:科学出版社,1958.

[105] 关肇直. 拓扑空间概论[M]. 北京:科学出版社,1958.

[106] 黎景辉,冯绪宁. 拓扑群引论[M]. 北京:科学出版社,1991.

[107] 沈荣鑫,林寿. 拓扑群中广义度量性质的一个注记[J]. 数学年刊,2009,A30(5):697-704.

[108] TKACHENKO M. Paratopological and semitopological groups vs topological groups[C]//HART K P, VAN MILL J, SIMON P. Recent Progress in General Topology III. Pairs:Atlantis Press,2014:803-859.

[109] 李丕余,谢利红,牟磊,等. 仿拓扑群和半拓扑群的若干专题[M]. 沈阳:东北大学出版社,2014.

[110] GRUENHAGE G. Generalized metric spaces[C]//KUNEN K, VAUGHAN J E. Handbook of Set-theoretic Topology. Amsterdam:Elsevier Science Publishers,1984:423-501.

[111] GRUENHAGE G, MICHAEL E A, TANAKA Y. Spaces determined by point-countable covers[J]. Pacific J Math,1984,113:303-332.

[112] 林寿,朱忠景. 几类度量空间映像的研究[J]. 数学进展,2013,42(2):129-137.

LIN Shou1,2

( 1.SchoolofMathematicsandStatistics,MinnanNormalUniversity,Zhangzhou363000,Fujian;

2.SchoolofMathematics,SichuanUniversity,Chengdu610065,Sichuan)

2010 MSC：54C10; 54D70; 54E18

(编辑 周 俊)

Fifty Years of Mappings and Spaces

A famous surveyMappingsandSpaceswritten by A. V. Arhangel’skiǐ in 1966 gave a powerful driving force to general topology, especially in the theory of generalized metric spaces. This paper provides an overview on its historical significance and practical function for general topology in fifty years, lists some open problems in the survey, and introduces some influence of recent Arhangel’skiǐ’s work for the development of general topology in China.

mutual classification of spaces and mappings; mapping; generalized metric space; weak base;p-space; topological algebra

2016-10-15

国家自然科学基金(11471153)

林 寿(1960—),男,教授,主要从事一般拓扑学的研究,E-mail:shoulin60@163.com

O189.1

A

1001-8395(2017)01-0133-10

10.3969/j.issn.1001-8395.2017.01.022