HAO Yapu, CHEN Huanyin

(School of Science, Hangzhou Normal University,Hangzhou 310036, China)

On Weakly J#-clean Rings

HAO Yapu, CHEN Huanyin

(School of Science, Hangzhou Normal University,Hangzhou 310036, China)

weakly J#-clean ring; clean ring; weakly nil clean;S=R[D,C] ring; idempotent; Jacobson radical

1 Introduction

Following W. K. Nicholson[1], we call a ringRis clean if every elementa∈Rcan be written in the form ofa=e+uwhereeis an idempotent anduis a unit. Later, A. J. Diesl[2]replaced units to nilpotent elements and then extended the clean rings to nil clean rings. A ringRis called a nil clean ring if every elementa∈Rcan be written in the form ofa=e+wwhereeis an idempotent andwis a nilpotent. Recently, S. Breaz, P. Danchev and Y. Zhou[3]introduced weakly nil clean rings. A ringRis called a weakly nil clean ring if every elementa∈Rcan be written in the form ofa=e+wora=-e+wwhereeis an idempotent andwis a nilpotent element. On the other hand, J-clean rings are studied by Chen[4]. A ringRis called a J-clean ring if every elementa∈Rcan be written in the form ofa=e+jwhereeis an idempotent andjbelongs to Jacobson radical. Recently, Shen[5]introduced weakly J-clean rings. A ringRis called a weakly J-clean ring if every elementa∈Rcan be written in the form ofa=e+jora=-e+jwhereeis an idempotent andjbelongs to Jacobson radical. Inspired by the weakly nil cleanness and J#-cleanness, we introduce a new type of ring. We call a ringRis weakly J#-clean if for anya∈R, there existse∈Id(R) such thata-e∈J#(R) ora+e∈J#(R). Here,J#(R)={x∈R|∃n, such thatxn∈J(R)}. We prove in the following that a ringRis weakly nil-clean if and only ifRis weakly J#-clean andJ(R) is nil. Then we imply that these rings are equivalent to each other with some other conditions. We also discuss various properties of such rings.

Throughout this paper, the rings that we discussed are associative rings with an identity.Id(R) denotes the idempotents ofR,J(R) denotes the Jacobson radicals ofR,J#(R)={x∈R|∃n, such thatxn∈J(R)},U(R) denotes the units ofR,N(R) denotes the nilpotent elements ofR,P(R) denotes the intersection of all prime ideals ofRand we useTn(R) to stand for the ring of alln×nupper triangular matrices over a ringR.

2 Examples

Definition 1 A ringRis called a weakly J#-clean ring if every elementa∈Rcan be written in the form ofa=e+jora=-e+jwheree∈Id(R) andj∈J#(R).

Proposition 1 IfN(R) forms an ideal, then every weakly J#-clean ring is clean ring.

Proof Leta∈Rthena=e+jora=-e+jwheree∈Id(R) andjn∈J(R) sinceRis weakly J#-clean. Ifa=e+jthena=(2e-1+j)+(1-e), (1-e)∈Id(R), as (2e-1)(2e-1)=1, we know that (2e-1) is a unit, so (2e-1+j)=(2e-1)[1+(2e-1)j]∈U(R) sinceN(R) forms an ideal, soais clean. Ifa=-e+jthena=(1-e)+(j-1) where (j-1)∈U(R) and (1-e)∈Id(R), soais clean. Therefore we get the result.

The following example shows that the converse of Proposition 1 is not true.

Example 1 Z5is a field, so Z5is clean. But Z5is not weakly J#-clean. As Z5is field, 0 and 1 are the all idempotents in Z5and 0 is the only element in the Jacobson radical of Z5, so 0+0=0,-0+0=0,1+0=1,-1+0=-1=4, we can see that 2 and 3 can not be written in the form ofe+jor -e+j. In conclusion, Z5is clean but not weakly J#-clean.

Following Shen[5], an elementaof a ringRis weakly J-clean in case there is an idempotente∈Rand a Jacobson radicalj∈Rsuch thata=e+jora=-e+j. Every weakly J-clean ring is weakly J#-clean. However weakly J#-clean rings maybe not weakly J-clean rings as the following shows.

Example 2M2(Z3) is weakly J#-clean, but it is not weakly J-clean.

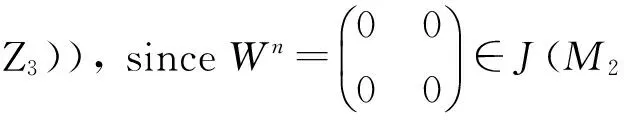
In fact, we have the following inclusions:J(R)J#(R)Rqnil

Remark1LetSbeacommutativeringandR=M2(S).By[7,Example4.3],wehaveJ#(R)=Rqnil.

Example5Herearesomeexamples:

1)AnyquotientofweaklyJ#-cleanringisweaklyJ#-clean.

2) R[x]iscertainlyneveraweaklyJ#-cleanasitisnotcleanring.

3) R[x]/(xn)isweaklyJ#-cleanifandonlyifsoisR.

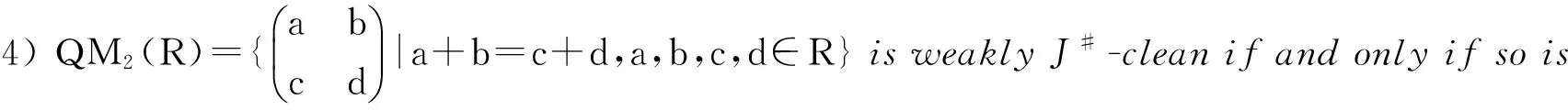
3 Elementary Propositions

Thefollowingtheoremrevealstherelationshipbetweenweaklynil-cleanringsandweaklyJ#-cleanrings.

Theorem1LetRbearing.ThenRisweaklynil-cleanifandonlyifRisweaklyJ#-cleanandJ(R)isnil.

ProofLeta∈J(R)thena=e+wora=-e+wwheree∈Id(R)andw∈N(R)sinceRisweaklynil-clean.Ifa=e+wthene=a-w, e=en=(a-w)n∈J(R), e=0.Soa=w, J(R)isnil.Similarly,ifa=-e+wthene=w-a.Wecanalsogeta=w, J(R)isnil.SoRisweaklyJ#-clean.

Conversely,ifRisweaklyJ#-clean,thenforanya∈R, a=e+jora=-e+jwheree∈Id(R)andj∈J#(R).AndJ(R)isnil,weget(jn)m=0,soj∈N(R).ThusRisweaklynil-clean.

AringRiscalledaJ#-cleanringifeveryelementa∈Rcanbewrittenintheformofa=e+jwheree∈Id(R)andj∈J#(R).

Theorem2LetRbeacleanring.ThenRisJ#-cleanifandonlyif

1) RisweaklyJ#-clean;

2) 2∈J(R).

ProofSupposeRisJ#-clean,itisobviousthatRisweaklyJ#-clean.Write2=e+jnwheree∈Id(R)andjn∈J(R). 1-e=jn-1∈U(R)isbothanidempotentandaunit,hencee=0, 2=jn∈J(R).So2∈J(R).

□

Thefollowingassertionisusefulforapplications.

Lemma1EveryhomomorphicimageofaweaklyJ#-cleanringisweaklyJ#-clean.

ProofItisobvious.

□

Theorem3LetRbeacleanring.ThenRisweaklyJ#-cleanifandonlyifR/J(R)isweaklynil-clean.

□

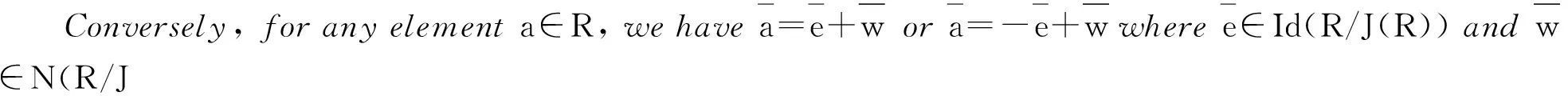
Corollary1LetRbearing.ThenRisJ#-cleanifandonlyif

1) Risclean;

2) R/J(R)isJ#-clean.

ProofSupposeRisJ#-clean, R/J(R)isJ#-cleansinceR/J(R)isthehomomorphicimageofR.Soeveryelement1+a∈Rcanbewrittenintheformof1+a=e+j,thatisa=e+(j-1)wheree∈Id(R)andjn∈J(R), jn-1∈U(R), j-1∈U(R).SoRisclean.

Theorem4LetRbearing.ThenRisweaklyJ#-cleanifandonlyifR/P(R)isweaklyJ#-clean.

ProofThenecessitybeinganelementaryconsequenceofLemma1.

□

Theorem5LetIbenilpotent.ThenRisweaklyJ#-cleanifandonlyifR/IisweaklyJ#-clean.

ProofThenecessitybeinganelementaryconsequenceofLemma1,weconcentrateonthesufficiency.Tothataim,leta∈R,thena+I∈R/Iandbyhypothesis, a+I=(b+e)+Iora+I=(b-e)+I,whereb+I∈J#(R/I)ande+I∈Id(R/I).AsIisnilpotent,itisobviousthatb∈J#(R).Asfore,itiswellknownthatidempotentsliftmoduloanynilideal,sothatthisfollowstoassumethate∈Id(R).So, RisweaklyJ#-clean,asdesired.

□

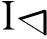
1)R/Iis weakly J#-clean ;

2)R/Inis weakly J#-clean for alln≥1.

Proof SupposeR/Iis weakly J#-clean. Write eithera+I=(b+I)+(e+I)=(b+e)+Iora+I=(b+I)-(e+I)=(b-e)+I, whereb+I∈J#(R/I) ande+I∈Id(R/I). AndIis an ideal ofR, soa+In=(b+e)+In=(b+In)+(e+In) ora+In=(b-e)+In=(b+In)-(e+In), whereb+In∈J#(R/In) ande+In∈Id(R/In). SoR/Inis weakly J#-clean for alln≥1.

Conversely, it is obvious when we choosen=1.

1)R/(IJ) is weakly J#-clean;

2)R/(I∩J) is weakly J#-clean.

Proof SupposeR/(IJ) is weakly J#-clean. SinceR/(I∩J)≅R/(IJ)/(I∩J)/(IJ) andR/(IJ)/(I∩J)/(IJ) is the homomorphic image ofR/(IJ), as required.

Conversely, (I∩J/IJ)2⊆(I∩J)(I∩J)/IJ⊆IJ/IJ=0. SoR/(IJ) is weakly J#-clean by Theorem 5.

1)R/(IJ) is J#-clean;

2)R/(I∩J) is J#-clean.

Proof By Corollary 3 and induction, we easily obtain this result.

□

4 Extensions

In this section, we further consider weak J#-cleanness for various related rings.

□

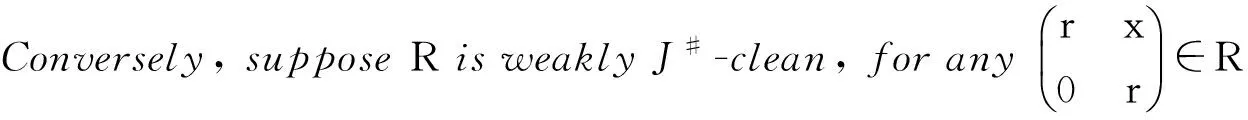
Theorem7LetRbearing.Thenthefollowingareequivalent:

(1) RisweaklyJ#-clean;

(2) R[[x]]isweaklyJ#-clean.

(1)⟹(2)Letf(x)=a0+a1x+a2x2+…∈R[[x]].SupposethatRisweaklyJ#-clean,fora0∈R,wehavea0=e+jora0=-e+jwheree∈Id(R)andj∈J#(R).Ifa0=e+j,thenf(x)=a0+a1x+a2x2+…=e+j+(a1x+a2x2+…)=e+α(x)whereα(x)=j+a1x+a2x2+….Similarly,ifa0=-e+j,thenf(x)=-e+α(x).Itiseasytoknowα(x)∈J#(R[[x]]),hence, R[[x]]isweaklyJ#-clean.

□

Corollary5LetRbearing.Thenthefollowingareequivalent:

1) RisweaklyJ#-clean;

2) R[[x1,x2,…xn]]isweaklyJ#-clean.

ProofByTheorem7andinduction,weeasilyobtainthisresult.

Theorem8LetRbearing.Thenthefollowingareequivalent:

(1) RisJ#-clean;

(2)Thereisanintegern≥1suchthatTn(R)isJ#-clean;

(3)Thereisanintegern≥2suchthatTn(R)isweaklyJ#-clean.

(2)⟹(3)Itisobvious.

□

Lemma2SupposeR=∏i∈IRiisadirectproductofringsRi≅Rforalli∈IsuchthatIisfiniteand|I|≥2.ThenRisweaklyJ#-cleanifandonlyifRiisJ#-clean.

ProofOnedirectionisobvious.IfRiisJ#-cleanforalli∈I,thenR=∏i∈IRiisJ#-clean,ofcourseitisweaklyJ#-clean.

Conversely,ifR=∏i∈IRiisweaklyJ#-clean.Weassumethereisani∈IsuchthatRiisweaklyJ#-clean,thenallRiareweaklyJ#-cleansinceRi≅R.Thusthereexistr1∈Ri1andr2∈Ri2suchthatr1≠e+jandr2≠-e+jwheree∈Id(R)andj∈J#(R).Thenwegetthat(r1,r2)isnotweaklyJ#-cleaninRi1×Ri2,acontradiction.

□

Theorem9LetRbearing.Thenthefollowingareequivalent:

(1) RisJ#-clean;

(2)Thereisanintegern≥1suchthat×nRisJ#-clean;

(3)Thereisanintegern≥2suchthat×nRisweaklyJ#-clean.

Proof(1)⟹(2)Foranyelement(a1,a2,...,an)∈×nR, aicanbewrittenintheformofai=ei+jiwhereei∈Id(R)andji∈J#(R)foranyi∈N*, 1≤i≤nsinceRisJ#-clean.Then(a1,a2,...,an)canbewrittenintheformof(a1,a2,...,an)=(e1,e2,...,en)+(j1,j2,...,jn)where(e1,e2,...,en)∈Id(×nR)and(j1,j2,...,jn)∈J#(×nR),so×nRisJ#-clean.

(2)⟹(3)Itisobvious.

(3)⟹(1)ByLemma2andinduction,weeasilyobtainthisresult.

□

Theorem10SupposeR=∏i∈IRiisadirectproductofringsRi≅Rforalli∈IsuchthatIisfiniteand|I|≥2.ThenRisweaklyJ#-cleanifandonlyifthereexistsk∈IsuchthatRkisweaklyJ#-cleanandRjisJ#-cleanforallj≠k.

ProofSupposethatRisweaklyJ#-clean.AsanimageofR,eachRiforalli∈IisweaklyJ#-cleanasaconsequenceofLemma1.Assumethatthereexisttwoindicesi1andi2suchthatneitherRi1norRi2areJ#-clean.Thenthereexistr1∈Ri1andr2∈Ri2suchthatr1≠e+jandr2≠-e+jwheree∈Id(R)andj∈J#(R).Thus(r1,r2)isnotweaklyJ#-cleaninRi1×Ri2,acontradiction.

Conversely,ifeveryRiisJ#-clean,byLemma2,soRisweaklyJ#-clean.SupposethatRkisweaklyJ#-cleanbutnotJ#-cleanandalltheotherRjareJ#-clean.Letx=(xi)∈R=∏i∈IRi,thenxk=jk+ekorxk=jk-ekwhereek∈Id(Rk)andjk∈J#(Rk).Ifxk=jk+ek,thenforj≠kandRjisJ#-clean,wemusthavexi=ji+eiwhereei∈Id(Ri)andji∈J#(Ri).Ifnowxk=jk-ek,thenforj≠kandRjisJ#-clean,wecanwritexi=ji-eiwhereei∈Id(Ri)andji∈J#(Ri).Therefore, xisweaklyJ#-cleaninR,asexpected.

□

LetDbearing, CbeasubringofDand1D∈C,write:

S=R[D,C]={(d1,...,dn,c,c,...)|di∈D,c∈C,n≥1}

S′=R{D,C}={(d1,...,dn,cn+1,cn+2,...)|di∈D,cj∈C,n≥1}

Lemma3 1) J(S)=R[J(D),J(D)∩J(C)]. 2) J(S′)=R{J(D),J(D)∩J(C)}.

Proof See [8, Theorem 2.1.14].

□

Lemma 4 LetS=R[D,C], thenDis isomorphic to an internal direct sum ofSandCis the epimorphism ofS.

Proof See [8, Proposition 2.1.1].

Theorem 11 The following conditions are equivalent:

(1)S=R[D,C] is weakly J#-clean;

(2) (a)Dis weakly J#-clean; (b)For anya∈C, there existsf∈Id(C), such thata+f∈J#(D)∩J#(C) ora-f∈J#(D)∩J#(C).

(3)S′=R{D,C} is weakly J#-clean.

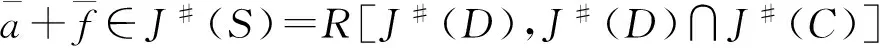
or

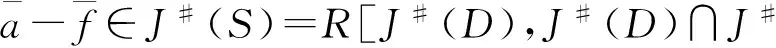
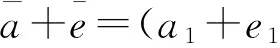
or

SoSis weakly J#-clean.

(3)⟺(2) It is similar to (1)⟺(2).

□

Corollary 6 IfS=R[D,C] is weakly J#-clean, thenDandCare weakly J#-clean.

ProofItisobviousthatDisweaklyJ#-cleanbyTheorem8.Forany

thereexistsanidempotente∈Rsuchthata+e∈J#(R)ora-e∈J#(R).Then

or

SoS=R[D,C]isaweaklyJ#-cleanring.

□

[1]NICHOLSONWK.Liftingidempotentsandexchangerings[J].TransactionsoftheAmericanMathematicalSocity,1977,229(5):269-278.

[2]DIESLAJ.Nilcleanrings[J].Algebra,2013,383(6):197-211.

[3] BREAZ S, DANCHEV P, ZHOU Y. Rings in which every element is either a sum or a difference of a nilpotent and an idempotent[J]. Journal of Algebra and Its Applications,2016,15(8):410-422.

[4] CHEN H Y. On strongly J-clean rings[J]. Comm Algebra,2010,38(10):3790-3804.

[5] SHEN H D, CHEN H Y. On weakly J-clean rings[J]. Journal of Hangzhou Normal University(Natiral Science Edition),2015,14(6):616-624.

[6] HARTE R E. On quasinilpotents in rings[J]. Panamerican Math,1991,1(1):10-16.

[7] WANG Z, CHEN J L. Pseudo Drazin inverses in associative rings and Banach algebras[J]. Linear Algebra Appl,2012,437(6):1332-1345.

[8] CHENG G P, CHEN J L. The Structure of RingR[D,C] and Its Characterizations[J]. Journal Nanjing University(Natural Sciences Edition),2007,24(1):20-28.

关于Weakly J#-clean环

郝亚璞, 陈焕艮

(杭州师范大学理学院，浙江 杭州 310036)

weakly J#-clean环；clean环；weakly nil clean 环；S=R[D,C]环；幂等元；Jacobson 根

2016-05-04

Foundation item：Supported by the Natural Science Foundation of Zhejiang Province (LY17A010018).

CHEN Huanyin(1963—)，male，Professor，Ph.D.，majored in algebra of basic mathematics. E-mail：huanyinchen@aliyun.com

10.3969/j.issn.1674-232X.2017.02.010

O153.3 MSC2010: 16U99,16N40,16U10 Article character: A

1674-232X(2017)02-0173-08

Received date：2016-05-25