陈垂福 杨晓翔

福州大学机械工程及自动化学院,福州,350000

一种考虑密度补偿的变过滤半径敏度过滤方法

陈垂福 杨晓翔

福州大学机械工程及自动化学院,福州,350000

固定过滤半径的敏度过滤方法可以有效解决棋盘格现象和网格依赖性，但处理后拓扑优化结果普遍存在边界扩散现象，图形边缘存在大量的灰度单元。提出了一种考虑密度补偿的变过滤半径敏度过滤方法，即正向补偿相对密度为0.5～1的单元，反向补偿相对密度为0～0.5的单元，同时在拓扑优化计算的后期逐步缩小过滤半径至1。结合固体各向同性惩罚微结构模型，利用经典结构柔度最小化算例验证可行性。研究结果表明，考虑密度补偿的变过滤半径敏度过滤方法能够消除棋盘格现象，体现了网格无关性，拓扑优化结果具有清晰的边界，且优化效率和优化效果明显提升。

拓扑优化；灰度单元；棋盘格现象；网格依赖性

0 引言

连续体结构拓扑优化中存在棋盘格现象和网格依赖性等数值不稳定问题，棋盘格现象和网格依赖性二者一般同时发生，能够消除棋盘格现象的方法一般情况下能够在一定程度上消除网格依赖性[1]。离散化采用高阶等参元和非协调元可以有效抑制棋盘格现象，周长约束法和局部梯度约束法可以抑制网格依赖性，但在优化问题中加入了额外的约束，造成问题求解困难[2]。SIGMUND等[3]提出的敏度过滤方法，按照邻域内单元与中心单元的距离进行加权平均以修改中心单元的目标函数敏度值，有效解决了棋盘格现象和网格依赖性问题，敏度过滤方法不附加额外的约束条件，在程序方面易于实现，该方法对拓扑优化结果进行处理后，拓扑图形边界存在大量的灰度单元。针对敏度过滤方法的缺陷，许多学者做了进一步的研究，在敏度过滤方法的基础上提出改进方案，如龙凯等[4]提出考虑密度梯度的敏度过滤方法，增加密度梯度加权函数项，使密度梯度大于设定阀值时权函数取值较小，修正敏度过滤方法中的距离权函数，获得了清晰的边界；朱剑峰等[5]通过设置中心单元过滤权重对拓扑优化结果进行控制，避免了拓扑优化结果被过度磨平。除此之外，张志飞等[6]采用双重固体各向同性惩罚微结构模型(solid isotropic microstructure with penalization，SIMP)方法，龙凯等[7]采用Heaviside函数改进优化准则法，均获得了清晰的拓扑优化结果。

本文针对SIGMUND等[3]的敏度过滤方法存在的边界扩散问题，在敏度过滤方法的基础上提出变过滤半径敏度过滤方法，该方法控制过滤半径在一定的迭代步数后迅速减小，使得边界的灰度单元逐渐减少，同时加入密度补偿公式，解决该方法局部位置出现少量孔洞的问题。考虑密度补偿的变过滤半径敏度过滤方法不仅能有效消除棋盘格现象和网格依赖性，且有效抑制了边界扩散现象，同时大幅度提高了优化速度，取得了更好的优化结果。通过经典的二维结构柔度最小化算例验证了本文方法的可行性。

1 变密度法拓扑优化建模

1.1 刚度-密度插值模型

固体各向同性惩罚微结构(SIMP)模型是目前工程上应用最广泛的材料插值模型，假设材料各向同性，泊松比υ为常量，SIMP模型假设材料弹性模量和密度满足以下关系：

(1)

式中，Ei(ρi)为单元i插值后的弹性模量；Emin为空洞材料的弹性模量，一般设为E0/1000；E0为材料原始的弹性模量；ρi为单元i的相对密度，0≤ρi≤1；p为SIMP模型引入的惩罚因子。

采用SIMP模型获得新单元的弹性模量，将结构整体刚度矩阵和整体刚度矩阵敏度信息表述为

(2)

(3)

式中，K为插值后结构的整体刚度矩阵；ki为单元i插值后的单元刚度矩阵；k0为单元相对密度为1时所对应的单元刚度矩阵。

1.2 经典算例结构拓扑优化数学模型及求解算法

基于SIMP模型建立柔度最小化问题的拓扑优化数学模型：

(4)

式中,C为整个结构的柔度值；U为结构位移列向量；N为单元数目；ui为单元i的位移列向量；V为优化后结构的体积；f为优化体积比分数；V0为优化前结构的体积；F为结构载荷列向量。

通常采用移动渐近线法(method of moving asymptotes,MMA)(或称移动近似算法)和优化准则法(optimality criteria,OC)求解变密度法拓扑优化问题，MMA算法适用于单约束问题和复杂目标函数多约束问题；OC算法收敛速度快，计算规模与求解变量的数目无关，计算过程中不需要使用导数信息，适用于单目标函数、单约束条件下优化问题的求解[8]。对于一定体积比约束下的柔度最小化问题，宜采用OC算法。

2 敏度过滤方法

2.1 Sigmund敏度过滤方法

Sigmund敏度过滤方法[9](以下简称Sigmund方法)采用数字图像过滤技术平滑优化结果，Sigmund方法的数学表达式为

(5)

其中Hi为卷积因子；rmin为最小过滤半径，dist(k,i)为单元k中心到单元i中心的距离。单元相对密度的取值为0到1，取ρmin=0.001，以免造成计算上的奇异性。

中心单元和过滤半径rmin确定的过滤区域内，卷积因子Hi的数值为非0，过滤区域外卷积因子的数值为0，在过滤区域内的单元才会对中心单元的目标函数敏度值产生影响。当过滤半径过小时，过滤区域内单元数目较少，中心单元的权重过大，消除棋盘格和网格依赖性效果不明显；过滤半径过大时，对中心单元产生影响的单元过多，各单元的卷积因子数值接近，导致拓扑优化结果模糊，拓扑图形被过度磨平。

为量化拓扑优化结果单元相对密度的离散度，引入离散度指标评价结果的清晰程度[10]，其数学表达式为

(6)

根据离散度的描述公式，当所有单元相对密度都为0或1时，离散度指标Sd数值为0；当所有单元的相对密度都为0.5时，离散度指标Sd数值为100%。

2.2 变过滤半径敏度过滤方法

Sigmund方法存在边界扩散现象的原因是，消除棋盘格现象和网格依赖性时，利用中心单元邻域内的单元根据距离的不同采用不同的权系数进行加权平均，当棋盘格现象和网格依赖性基本消除即拓扑结构的主体框架形成时，过滤半径仍然保持不变，导致中心单元继续受邻域内的单元影响，对于边界上的单元，邻域内的单元多数为相对密度为0的单元，因此在边界上产生了大量的灰度单元，形成了边界扩散现象。

变过滤半径敏度过滤方法的思路是：在拓扑优化计算的初期，保持大过滤半径，保证完全消除棋盘格现象和网格依赖性，拓扑结构的主体框架形成后控制过滤半径逐步减小，逐步消除边界上的灰度单元，最终使得过滤半径为1，单元相对密度不再受周围单元影响。

根据上述思路，假设过滤半径rnew和迭代步数相关，建立如下函数关系：

(7)

过滤半径rnew和迭代步数l的关系如图1所示。

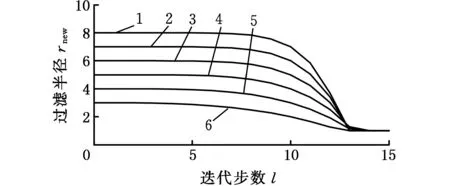
(a)衰减系数a=10

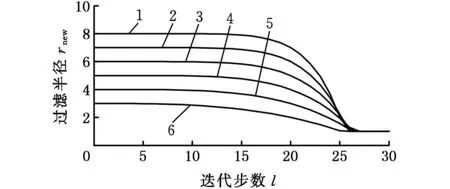
(b)衰减系数a=20

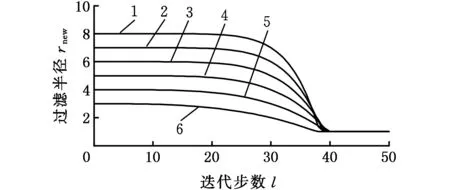
(c)衰减系数a=30

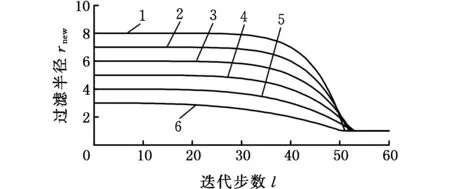
(d)衰减系数a=40图1 过滤半径rnew变化曲线Fig.1 Curve of filter radius rnew

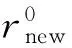
拓扑优化数值模拟实验结果表明，一般情况下大约在迭代步数l=12时形成了拓扑结构的主体框架，之后需要在一定的迭代步数内保持大的过滤半径使得主体框架稳定，防止主体结构在计算后期发生变化。衰减系数a过小，容易在局部位置出现棋盘格现象或者细小分枝结构;衰减系数a过大会增加迭代步数，取衰减系数a=20可在大部分的算例中得到满意的结果。

2.3 一种密度补偿方法

变过滤半径敏度过滤方法计算局部细节处存在较多灰度单元的算例时会出现少量的小孔结构，如图2a所示，Sigmund方法计算产生的结构存在A、B和C三处灰度单元较多的位置，在变过滤半径敏度过滤方法的计算结果(图2b)中，相应地在图2a所示的三个位置处出现少量孔洞。

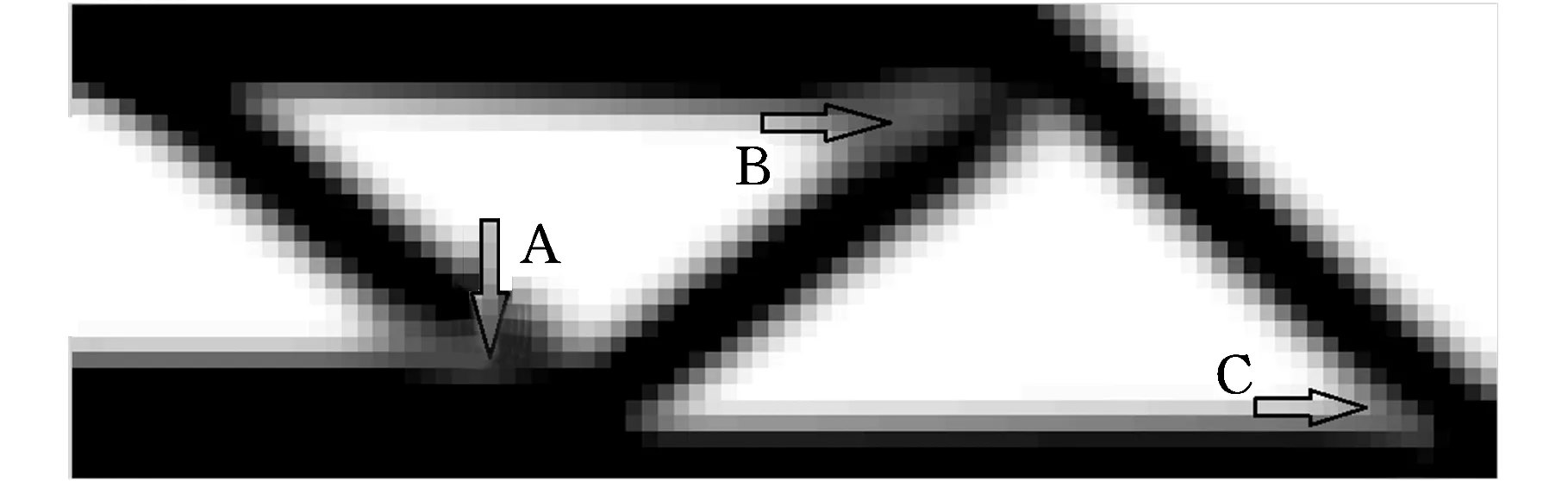
(a)Sigmund方法灰度结构位置示意图

(b)变过滤半径敏度过滤方法拓扑优化结果图2 变过滤半径敏度过滤方法缺陷说明图Fig.2 Disadvantage schematic of variable filter radius sensitivity filter method

微小孔洞是由于SIMP模型对单元相对密度的惩罚特性造成的，SIMP模型表示的刚度-密度关系如图3所示。

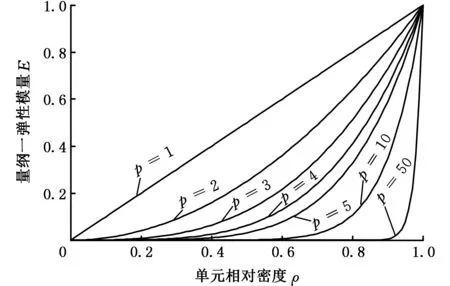
图3 不同惩罚因子下SIMP模型曲线Fig.3 Curve of SIMP model using different penalty factors

由图3 可以看出，惩罚因子p的取值越大，相对密度ρ趋于两极化的效果越明显，无论惩罚因子p取多大值都会使得单元相对密度ρ<1的大部分中间密度单元趋于0，可以明显地看出相对密度在0.8以下的单元会迅速地趋于0。相对密度在0.5～0.8之间的单元迅速趋于0是不合理的[11]，该密度区间的单元过快地趋于0，导致图2所示灰度单元较多的位置由于过滤半径减小至1，中心单元不再受周围单元影响而出现孔洞结构。必须使得相对密度大于0.5的单元经过多次迭代逐步趋于两极化，才能保证最优拓扑的搜索，防止微小孔洞出现。

为了补偿单元相对密度处于0.5～0.8之间的单元，保证该密度区间的单元能够经过多次迭代逐步趋于两极化，并加快单元相对密度小于0.5的单元趋于0，进一步提高优化速度，提出一种单元相对密度的补偿方法，其数学表达式为

(8)

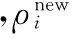
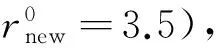
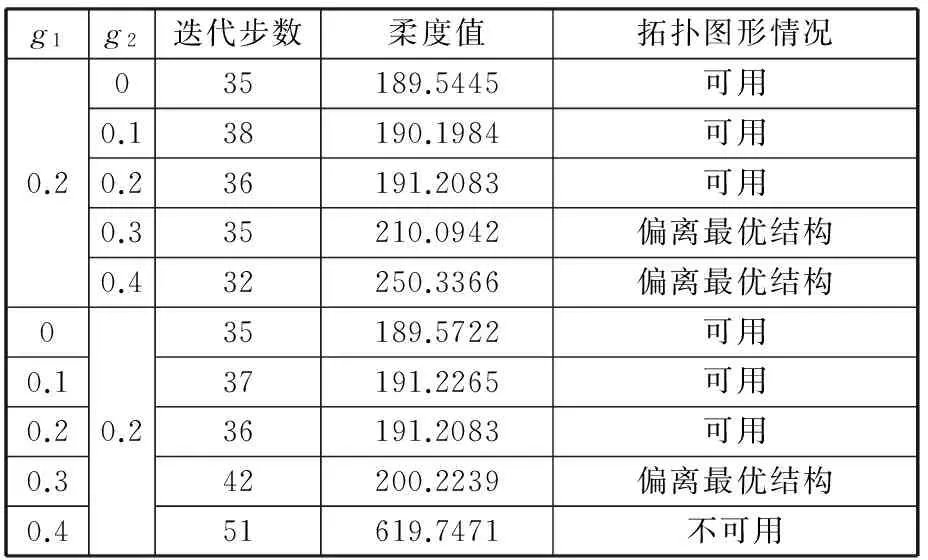
表1 不同密度补偿系数下MBB梁计算结果

由表1数据可发现，g1为固定值时，g2过大会使得拓扑结构逐步偏离最优结构，所得结构柔度值增大，g2的可行范围为0～0.2；g2为固定值时，g1过大会使得结构逐步偏离最优拓扑结构或获得不可行解，g1的可行范围为0～0.2。通过大量算例实验发现g1=0.2、g2=0.2时大部分算例均可获得有效可行解。

3 二维算例分析与讨论

采用经典拓扑优化算例验证考虑密度补偿的变过滤半径敏度过滤方法(简称本文方法)的可行性，通过MATLAB R2012a编写程序进行计算[12-13]，算例模型均采用平面四节点四边形单元进行离散化，对模型的材料属性和结构尺寸进行量纲一化处理，设弹性模量E=1，泊松比υ=0.3，SIMP模型惩罚因子p=3。

3.1 算例1模型优化及讨论

算例1 模型如图4所示，梁尺寸为240×40×1，顶部中点受垂直向下载荷F=1。考虑模型的对称性，采用1/2模型进行拓扑优化计算，1/2模型网格密度为120×40；为比较不同约束条件下的优化结果，设目标函数为整体结构的柔度最小化，约束条件分别40%、50%和60%的体积比约束。

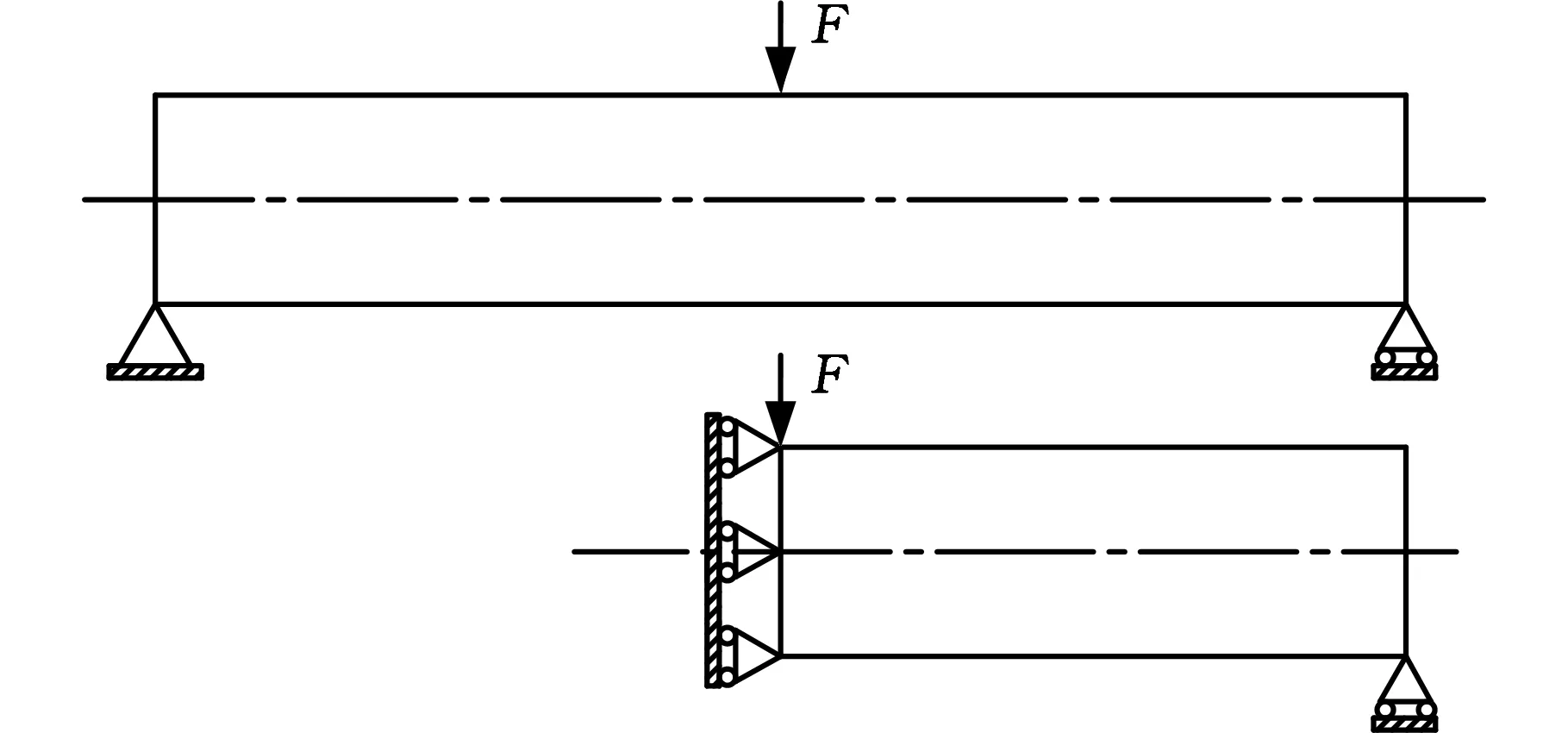
图4 算例1模型示意图Fig.4 Model of test problem 1

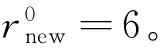
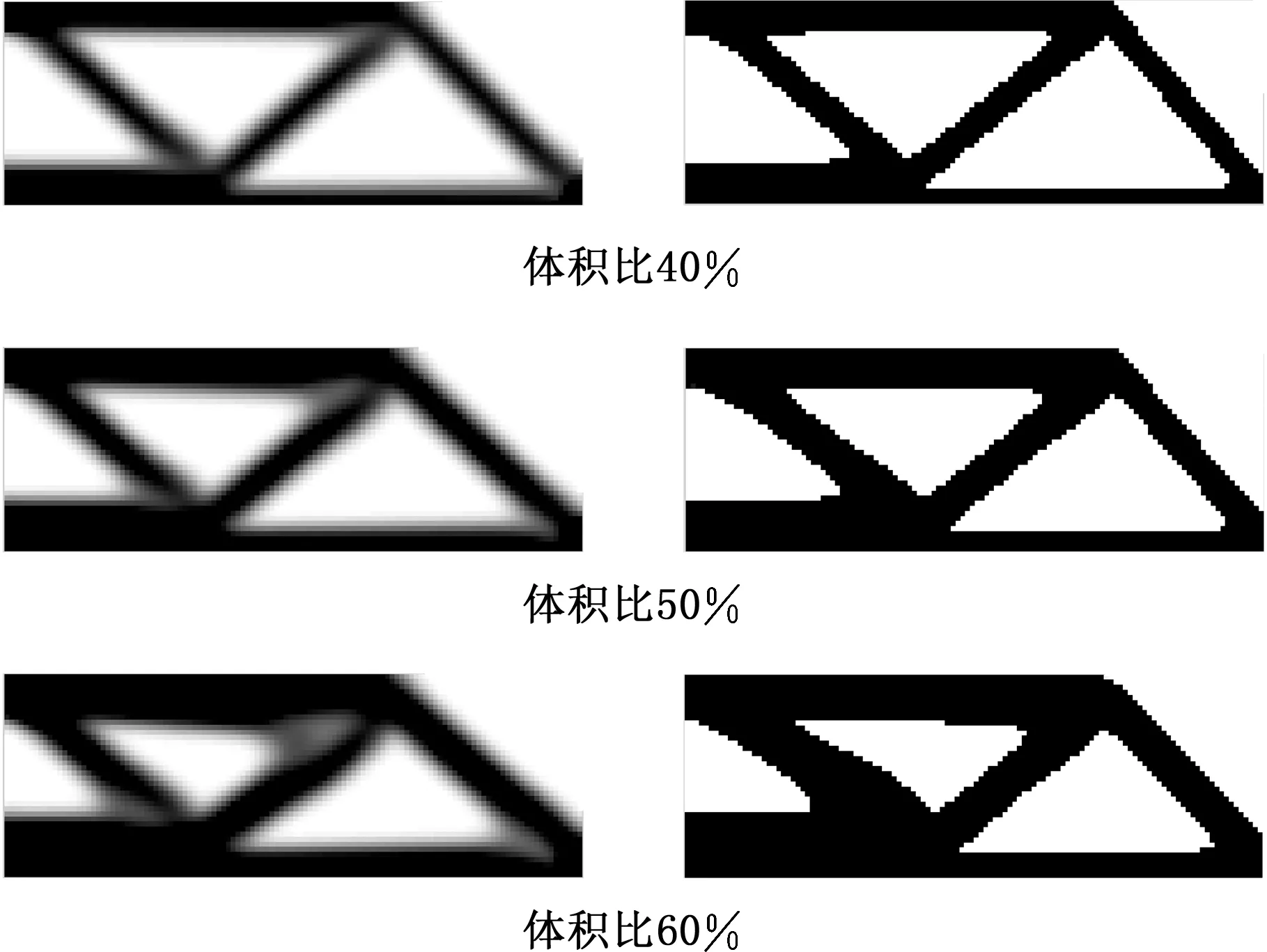
(a)Sigmund方法 (b)本文方法图5 算例1不同敏度过滤方法最优拓扑结果对比Fig.5 Comparison of topology results using different sensitivity filter methods(test problem 1)

由图5可以看出，不同过滤方法产生的拓扑优化结果相似，Sigmund方法由于过滤半径保持不变，在图形边界存在大量的灰度单元，造成拓扑结果边界模糊。本文方法由于在完成主体框架搜索后过滤半径逐步减小至1，拓扑结果边界清晰，不同体积比约束下的优化结果的离散度指标均小于0.2%，较相同约束的Sigmund方法大幅度降低；从Sigmund方法体积比约束为60%的结果来看，图形开始出现发展其他分枝结构的趋势，进一步增大过滤半径能够抑制这个趋势，但势必会导致灰度单元进一步增多，本文方法在60%的体积比约束下，仍然保持清晰的主体结构不变，并未出现其他分枝结构；从优化效果来看，不同的体积比约束下，本文方法所得到的结构的柔度值较Sigmund方法大幅度减小，优化效果明显提升；从优化效率来看，本文方法的迭代步数与Sigmund方法相比，减小了至少50%，节省了大量的计算时间。

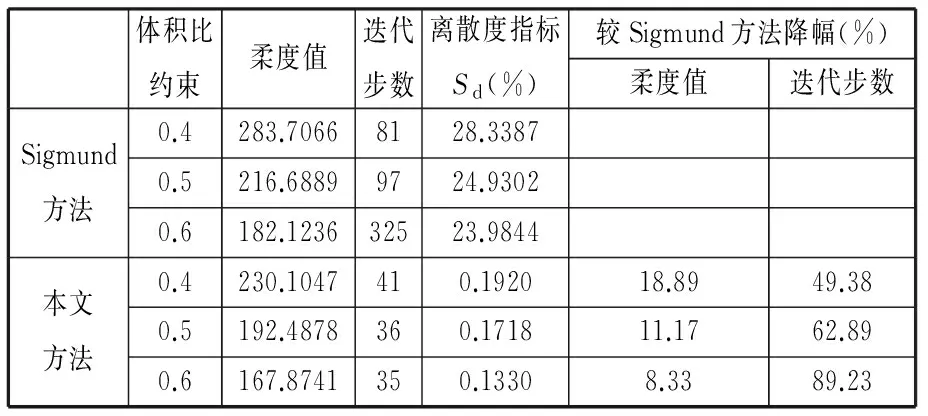
表2 算例1不同敏度过滤方法最优拓扑结果对比

为了验证本文方法能否有效消除网格依赖性，将算例1的1/2模型离散为210×70网格(1.75倍网格密度)，体积比约束设为40%，优化迭代步数为43步，柔度收敛值为230.3730，离散度指标为 0.1983%，拓扑优化结果如图6所示。

图6 算例1本文方法拓扑优化结果(210×70网格)Fig.6 Result of test problem 1 using the paper method(210×70)

对比图6和图5b中40%体积比约束的优化结果，两种网格密度的计算结果相似，210×70网格离散情况下，未出现细小的分枝结构，体现了网格无关性，迭代步数并未随着网格密度的增加而增加，且仍然保持着清晰的拓扑图形边界。

3.2 算例2模型优化及讨论

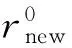
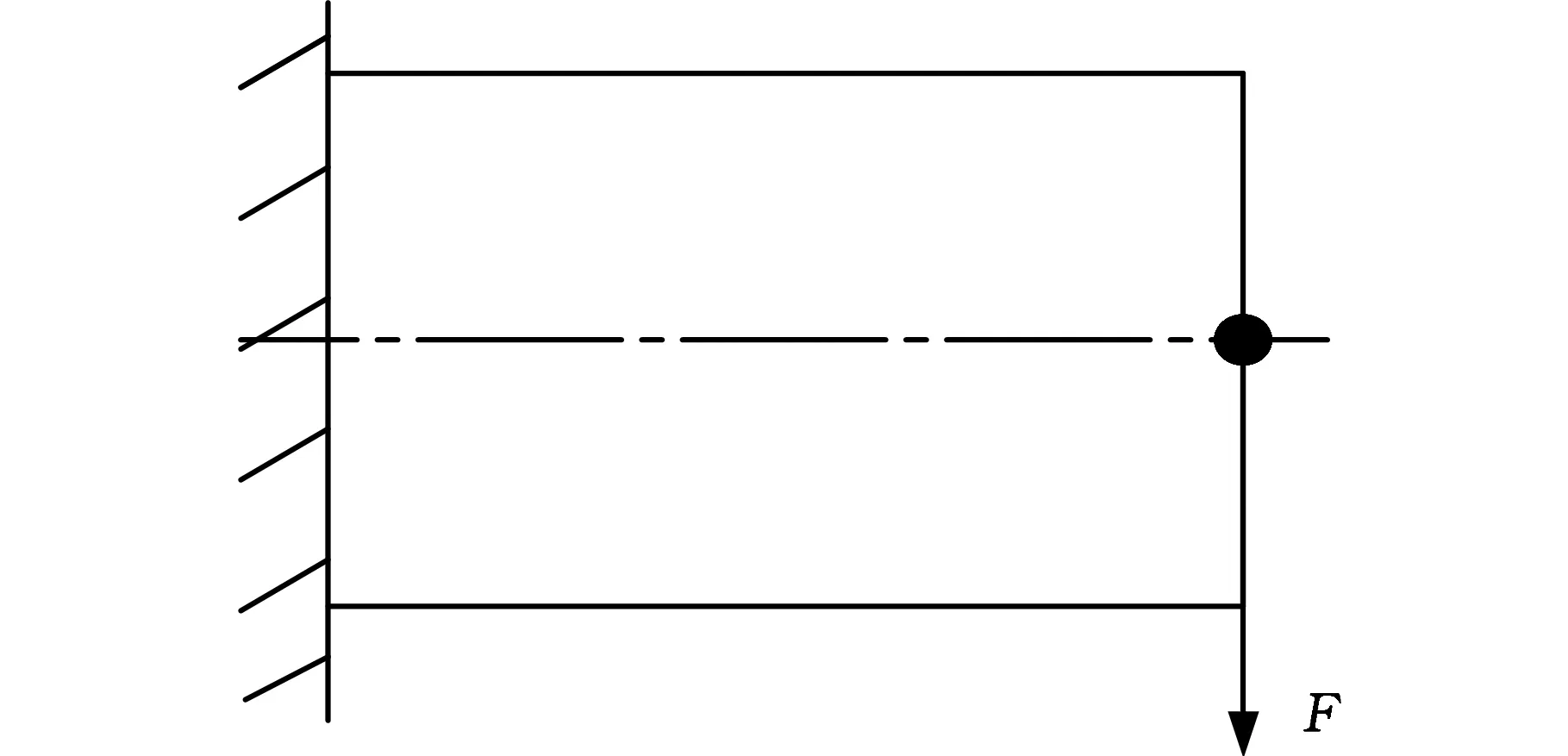
图7 算例2模型示意图Fig.7 Model of test problem 2

(a)Sigmund方法

(b)本文方法

(c)本文方法图8 算例2不同敏度过滤方法最优拓扑结果对比Fig.8 Comparison of topology results using different sensitivity filter methods(test problem 2)

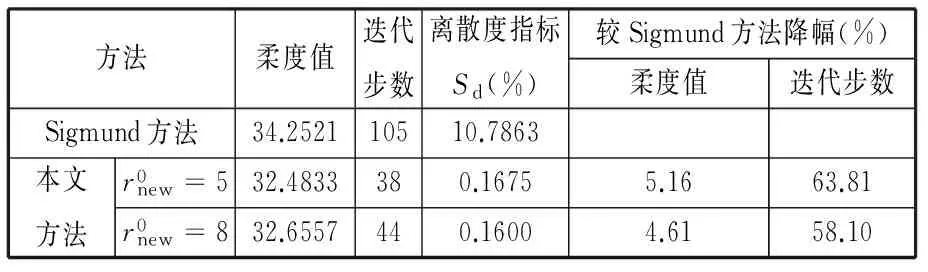
表3 算例2不同敏度过滤方法最优拓扑结果对比

由图8和表3可以看出，本文方法过滤半径取5和8的拓扑优化结果图形与Sigmund方法相似，基本消除了边界扩散现象，离散度均小于0.2%，有效地抑制了灰度单元的产生。计算得到的柔度值小于Sigmund方法的柔度值，迭代步数大幅度减少。

Sigmund方法对过滤半径的取值没有明确规定，仅认为过滤半径包含制造最小尺寸的含义，一般取单元边长尺寸的1～3倍，过滤半径的取值存在较大的波动，所得的优化结果边界模糊程度不同，难以准确地确定一个最小的过滤半径来保证所得拓扑结果最优(边界扩散程度最低)。而本文方法采用变过滤半径的策略，不同的初始过滤半径可以得到相似且边界清晰的拓扑优化结果，因此取较大的初始过滤半径也可保证得到的优化结果模糊程度最低。由图9可以看出，本文方法的离散度曲线存在两处明显的下降。第一次下降的原因与Sigmund方法相同，是由于拓扑结构逐步形成所导致的；第二次下降是由于过滤半径逐步减小，使得灰度单元的数量减少导致的，而离散度第二次下降的迭代步数在20步左右，对应着图1b中过滤半径在迭代步数为20时逐步减小至1的趋势。本文方法的变过滤半径策略能够有效地减少灰度单元，得到清晰的拓扑图形，拓扑结果的准确度和优化效率明显优于Sigmund方法。

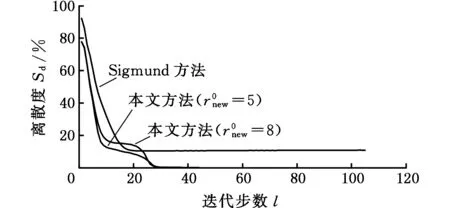
图9 算例2离散度变化曲线Fig.9 Curve of element density dispersion(test problem 2)

4 结论

本文提出一种考虑密度补偿的变过滤半径敏度过滤新方法，考虑SIMP模型的缺陷，对不同密度区间的单元进行双向补偿，进一步加速单元相对密度的两极化。采用变过滤半径的策略改进Sigmund敏度过滤方法，一定网格密度范围内的离散情况可采用相同的初始过滤半径，均可以消除棋盘格现象和网格依赖性，得到相似且清晰的拓扑优化结果。同时本文方法的优化迭代步数较Sigmund敏度过滤方法大幅度减少，优化效果明显提高。

[1]SIGMUNDO,PETERSSONJ.NumericalInstabilitiesinTopologyOptimization:aSurveyonProcedureDealingwithCheckerboards,Mesh-DependenciesandLocalMinima[J].StructuralOptimization, 1998, 16 (1):68-75.

[2] 左孔天. 连续体结构拓扑优化理论与应用研究 [D]. 武汉: 华中科技大学, 2004.ZUOKongtian.ResearchofTheoryandApplicationaboutTopologyOptimizationofContinuumStructure[D].Wuhan:HuazhongUniversityofScienceandTechnology, 2004.

[3]SIGMUNDO,MAUTEK.SensitivityFilteringfromaContinuumMechanicsPerspective[J].StructuralandMultidisciplinaryOptimization, 2012, 46(4): 471-475.

[4] 龙凯，傅晓锦.考虑密度梯度的敏度过滤方法[J].计算机辅助设计与图形学学报,2014,26(4):669-674.LONGKai,FUXiaojin.SensitivityFilteringMethodConsideringDensityGradient[J].JournalofComputer-AidedDesign&ComputerGraphics,2014,26(4):669-674.

[5] 朱剑峰, 林逸, 陈潇凯, 等. 连续体结构拓扑优化改进的敏度修正方法研究[J]. 中国机械工程, 2014, 25(11): 1506-1510.ZHUJianfeng,LINYi,CHENXiaokai,etal.ResearchonImprovedSensitivityModificationMethodofContinuumTopologyOptimization[J].ChineseMechanicalEngineering,2014, 25(11): 1506-1510.

[6] 张志飞, 徐伟, 徐中明, 等. 抑制拓扑优化中灰度单元的双重SIMP方法[J]. 农业机械学报, 2015, 46(11): 405-410.ZHANGZhifei,XUWei,XUZhongming,etal.Double-SIMPMethodforGray-scaleElementsSuppressioninTopologyOptimization[J].TransactionsoftheChineseSocietyforAgriculturalMachinery,2015, 46(11): 405-410.

[7] 龙凯, 赵红伟. 抑制灰度单元的改进优化准则法[J]. 计算机辅助设计与图形学学报, 2010,22(12): 2197-2201.LONGKai,ZHAOHongwei.AModifiedOptimalityCriterionMethodforGrayElementsSuppression[J].JournalofComputer-AidedDesign&ComputerGraphics, 2010,22(12): 2197-2201.

[8] 左孔天,王书亭,张云清,等.拓扑优化中两类不同优化数值算法研究[J].华中科技大学学报,2004,32(9):63-65.ZUOKongtian,WANGShuting,ZHANGYunqing,etal.TwoTypesofAlgorithmsUsedinTopologyOptimization[J].JournalofHuazhongUniversityofScienceandTechnology(NaturalScienceEdition),2004,32(9):63-65.

[9]SIGMUNDO.DesignofMaterialsStructuresUsingTopologyOptimization[D].Copenhagen:TechnicalUniversityofDenmark, 1994.

[10]SIGMUNDO.Morphology-basedBlackandWhiteFiltersforTopologyOptimization[J].StructuralandMultidisciplinaryOptimization, 2007, 33(4/5): 401-424.

[11] 康昌俊, 段宝岩. 连续体结构拓扑优化的一种改进变密度法及其应用[J]. 计算力学学报, 2009, 26(2): 188-192.KANGChangjun,DUANBaoyan.AnImprovedVariableDensityMethodandApplicationforTopologyOptimizationofContinuumStructures[J].ChineseJournalofComputationalMechanics,2009, 26(2): 188-192.

[12]SIGMUNDO.A99LineTopologyOptimizationCodeWrittenMatlab[J].StructuralandMultidisciplinaryOptimization, 2001,21(2):120-127.

[13]ANDREASSENE,CLAUSENA,SCHEVENELSM,etal.EfficientTopologyOptimizationinMATLABUsing88LinesofCode[J].StructuralandMultidisciplinaryOptimization, 2011, 43(1): 1-16.

(编辑 苏卫国)

Variable Filter Radius Sensitivity Filtering Method Considering Density Compensation

CHEN Chuifu YANG Xiaoxiang

College of Mechanical Engineering and Automation,Fuzhou University,Fuzhou,350000

Constant filter radius sensitivity filtering method could effectively eliminate checkerboard patter and mesh dependence, the optimized results had boundary diffusion, the edges of the graph existed many gray-scale elements.A considering density compensation variable filter radius sensitivity filtering method was proposed as an efficient approach,compensated the elements of relative density in 0.5-1, and reduced element density value in 0-0.5, and gradually reduced the filter radius to 1. Combining the solid isotropic microstructure with penalization model(SIMP), the classical topology optimization problems were used to prove the superiority of the new method.The experimental results show that the new sensitivity filtering method may eliminate checkerboard patter and mesh independence,then the optimized results have clear boundary, and the optimization efficiency and optimization performance are improved significantly.

topology optimization; gray-scale element; checkerboard patter; mesh dependence

2016-05-06

国家自然科学基金资助项目(11372074)

U463;O39

10.3969/j.issn.1004-132X.2017.06.006

陈垂福，男，1991年生。福州大学机械工程及自动化学院硕士研究生。主要研究方向为连续体结构拓扑优化。E-mail:fdchenchuifu@163.com。杨晓翔，男，1963年生。福州大学机械工程及自动化学院教授、博士研究生导师。