一类Omega模型的期望折现罚金函数
2016-12-28王秀莲
周 颖, 王秀莲
(天津师范大学 数学科学学院, 天津 300387)
一类Omega模型的期望折现罚金函数
周 颖, 王秀莲
(天津师范大学 数学科学学院, 天津 300387)
在经典风险模型的基础上,根据公司盈余的正负不同收取不同的保费,考虑期望贴现罚金函数。首先,通过全概率公式得到了实质性破产时间的期望折现罚金函数满足的积分微分方程。在索赔分布函数为指数函数时导出了期望折现罚金函数满足的微分方程。最后,在罚金函数为指数函数时选取常见的三种破产率函数,将微分方程变化为库默尔方程,得出期望折现罚金函数具体的表达式。
Omega模型; 破产率函数; 期望折现罚金函数; 库默尔方程
在经典风险模型中保险公司的盈余过程可表示为[1]:
(1)
其中x=C(0)≥0是初始盈余;c是一个大于零的常数,表示保险公司单位时间内收取的保费率;{N(t)}t≥0表示t时刻累计发生索赔的次数是一个强度为λ的齐次泊松过程;Yi表示保险公司的第i次索赔,{Yi,i=1,2,…} 为独立同分布的非负随机变量序列,其分布函数为FY(x),密度函数为fY(x);{N(t)}t≥0与{Yi,i=1,2,…} 相互独立。对应期望折现罚金函数为:
mδ(x)=E[e-δτw(C(T-),|C(T)|)I{T<+∞}|C(0)=x],x≥0,
(2)
其中δ≥0是折现因子;T是破产发生的时间(盈余首次为负的时间);C(T-)是破产时刻之前的盈余,|C(T)|是破产时的赤字;I{·}表示示性函数;w(C(T-),|C(T)|)是一个罚金函数,依赖于破产时的立即盈余和赤字,一般设为连续函数。罚金函数w(C(T-),|C(T)|)在不同情况下可以表现为不同的表达形式,如:Albrecher等[2]在保费率恒定且破产率函数ω(x)=1的情况下研究了罚金函数w(x1,x2)=e-γ2x2时的期望罚金函数;Albrecher等[3]在保费率不变且破产率函数ω(x)=1的情况下研究了罚金函数w(x1,x2)=1时的期望折现罚金函数(即实质性破产的概率);Gerber等[4]研究了罚金函数为w(U(t))时的期望折现罚金函数。
对于经典风险模型,通常学者们研究的一个主要任务是计算期望折现罚金函数,即Gerber-shiu函数如(2)式;其中保险公司破产是指盈余首次为负值时,即破产时间T=inf{t>0|C(t)<0} 。但是实际生活中,有时保险公司的资金为负值时,公司可能会采取一些措施,比如:保险公司向银行贷款、提高保费率、延迟支付索赔等,使得公司即使出现赤字也能度过难关继续运营,直到发生实质性破产。针对实质性破产,风险理论的研究中出现了新的破产模型——Omega模型(Albrecher等[5]),在这个模型中实质性破产发生的概率依赖于一个破产率函数ω(x)(x≤0表示公司负盈余值),ω(x)dt表示在dt时间内公司资金为x时发生实质性破产的概率;一般情况下,假设ω(x)≥0,且当x
保费在保险经营中也是至关重要的一部分。保险的目的是针对可能出现的意外风险从经济上缓解损失,保险公司一般通过收取保费来增加收入,因理赔及常规管理造成支出。在经典风险模型中,保险公司收取的保费一般是关于时间的线性函数,即保费率视为固定的常数。实际上,保险公司的保费率可能会受一些因素影响而发生变换,比如:保险公司的盈余、保险公司索赔的次数、国家经济状况等。如:郑灿亮[7]和Jasiulewicz[8]研究了保费率受盈余大小影响时的破产概率;LU Yi等[9]研究了马氏调制风险模型中保费受环境影响时的破产概率。
本文考虑罚金函数仅与赤字有关的条件下,讨论Omega模型中保费值与公司盈余正负相关时的期望折现罚金函数。假设当盈余为正值时,保险公司收取一定的保费率;一旦盈余为负值时,公司通过提高保费率来降低破产发生的概率。
1 期望折现罚金函数
在Omega模型中,因为公司的盈余可以为负值,且本文考虑罚金函数仅与赤字有关,所以定义期望折现罚金函数为:
mδ(x)=E[e-δτw(|C(τ)|)I{τ<+∞}|C(0)=x],x∈R,
其中τ表示实质性破产发生的时间(实际生活中即为保险公司倒闭的时间)。
定理 假设x≥0时保费率为c1,x<0时保费率为c2,则期望折现罚金函数满足下面的积分微分方程:
证明 考虑在很小的时间区间(0,h)内,以是否有索赔到达或发生实质性破产为条件,由全概率公式有:当x≥0时,
mδ(x)=e-δhe-λhmδ(x+c1h)+∫0he-δtλe-λt∫0+∞mδ(x+c1t-y)dFY(y)dt,
(3)

mδ(x)=e-δhe-λh-∫0hω(x+c2y)dymδ(x+c2h)+∫0he-δtw(-(x+c2t))e-λtω(x+
c2t)e-∫0tω(x+c2y)dydt+∫0he-δte-∫0tω(x+c2y)dyλe-λt∫0+∞mδ(x+c2t-y)dFY(y)dt。
(4)
考虑(3),(4)式,当x→0且令h→0可以得到:
mδ(0+)=mδ(0-),
(5)
故mδ(x)在x=0处连续。
(3),(4)式先关于h求导再令h→0得到:
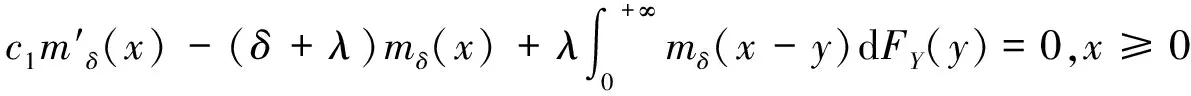
(6)
(6),(7)式对x→0,再由(5) 式的连续性得:
(8)
故mδ(x)在x=0处不可导。

且满足:
mδ,u(0+)=mδ,l(0-)。
(11)
求解微分方程(10)和(11)时,需确定索赔分布FY、折现罚金函数w(-x)和破产率函数ω(x);以下将针对索赔分布和罚金函数为指数函数时,选取3种常见的破产率函数进行计算。
2 指数索赔情况下期望折现罚金函数
2.1 期望折现罚金函数满足的积分微分方程
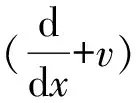
(12)
(w(-x)ω′(x)-w′(-x)ω(x)+vw(-x)ω(x))=0,x<0。
(13)
(12)式是一个二阶齐次线性微分方程,其特征方程为:
(14)
故可设方程的解为:
mδ,u(x)=A1e-Rux+B1eρux,x≥0,
(15)
其中A1,B1∈R,且-Ru<0,ρu>0是特征方程(14)的两个根。
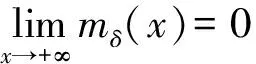
mδ,u(x)=A1e-Rux,x≥0。
(16)
对于(13)式,它是一个变系数微分方程,其对应齐次方程的系数中包含ω(x),故其解是不容易得到的。下面对给定的ω(x),w(-x)函数对方程(13)的解进行讨论。
2.2 特殊破产率函数的具体计算
2.2.1 常数破产率函数时的情况
当ω(x)=ωc,w(-x)=eqx,q>0时,方程(13)变为:
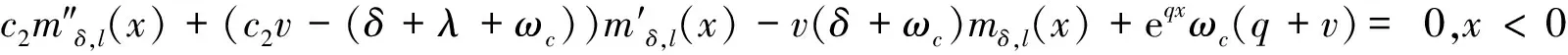
(17)
方程(17)对应齐次方程的特征方程为:
(18)
则方程(17)的解可设为:
mδ,l(x)=A2e-Rlx+B2eρlx+D2eqx,x<0,

mδ,l(x)=B2eρlx+D2eqx,x<0。
(19)
把(19)式代入方程(10),通过eqx项的系数关系可得:
另一方面把(16),(19)式代入方程(9),通过e-vx项的系数关系得:
(20)
(16),(19)式由连续条件(11)得:
A1=B2+D2,
(21)
由(20),(21)式可解出A1、B2为:
期望折现罚金函数为:
2.2.2 线性破产率函数时的情况
当ω(x)=-ax,w(-x)=eqx,q>0时,方程(13)变为:
(a-v(δ-ax))mδ,l(x)-(ax(q+v)+a)eqx=0,x<0,
(22)
方程(22)对应的齐次方程为:
(23)
该方程是一个变系数微分方程,将其进行化简:
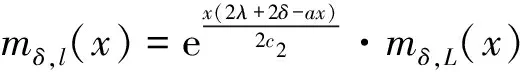
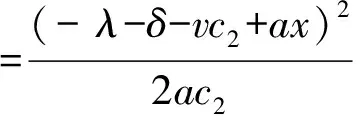
解库默尔方程可得解为:
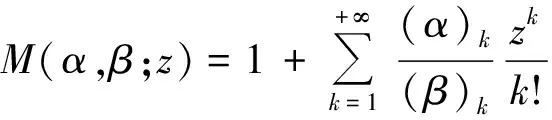
则方程(23)的解为:
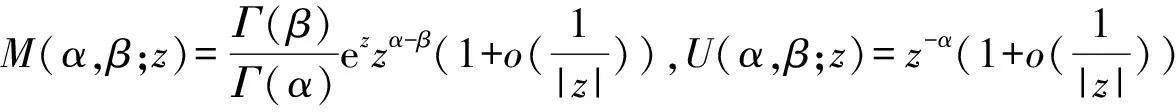
(24)
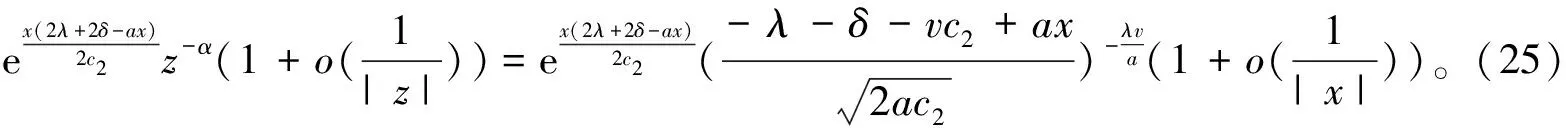
令
,
则由常数变易法,我们可以求出方程(22)的一个特解:
方程(22)的解为:
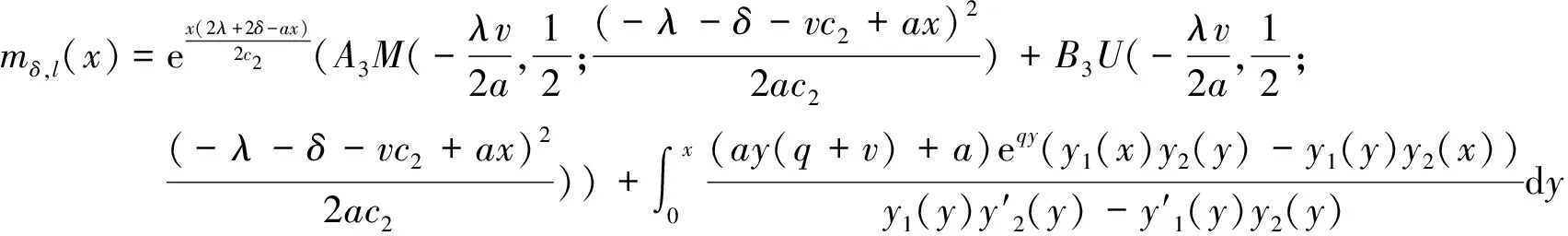
当x→-∞时,(24)式是无界的,(25)式趋于0;而x→-∞时,mδ,l(x)函数是有界的,故A3=0,则
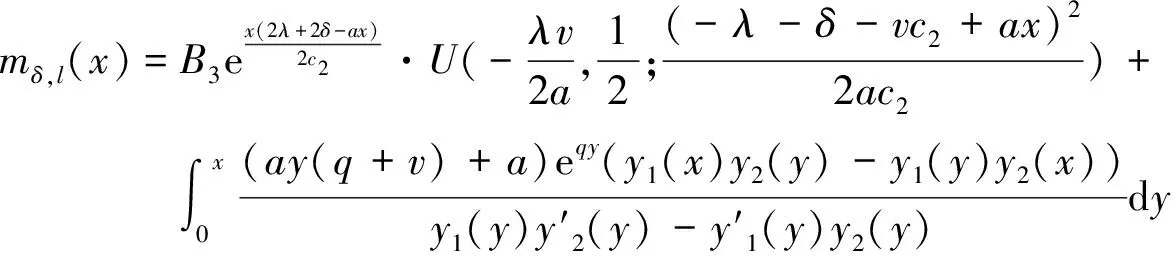
(26)
把(16)和(26)式带入方程(9)中,并取x=0得:
(27)
(16),(26)式再由连续条件(11)可得:
(28)
期望折现罚金函数的表达式为:
mδ(x)=
2.2.3 指数破产率函数时的情况
当ω(x)=e-ax,w(-x)=eqx,a,q>0时,方程(13)变为:
方程(29)对应的齐次方程为:
方程(30)的解法与方程(23)的解法相似,
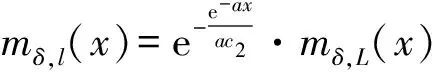
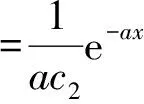
库默尔方程的解为:
其中A4、B4∈R。则方程(30)的解为:
且有

(31)
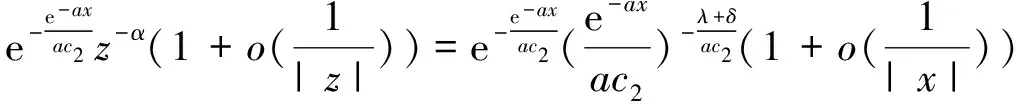
(32)
令
同样由常数变易法,我们可以求出方程(29)的一个特解:
方程(29)的解为:
当x→-∞时,(31)式是无界的,(32)式趋于0;而x→-∞时,mδ,l(x)函数是有界的,故A4=0,则
(33)
(16),(33)式再由条件(8)和连续条件(11)可得:
解得:
期望折现罚金函数的表达式为:
3 结 论
本文研究了Omega模型下保费大小与盈余正负有关时期望折现罚金函数问题,利用相关风险理论和概率知识,得到了期望折现罚金函数满足的积分微分方程,再通过给出索赔密度函数、罚金函数和破产率函数,最终得到了期望折现罚金函数的明确表达式,为进一步研究期望折现罚金函数问题奠定了一定的基础。
[1] GERBER H U,SHIU E S W.On the time value of ruin[J].North American Actuarial Journal,1998,2(1):48-72.
[2] ALBRECHE H,CHEUNG E C K,THONHAUSER S.Randomized observation Times for the compound Poisson risk model:the discounted penalty function[J].Scandinavian Actuarial Journal,2013,2013(6):424-452.
[3] ALBRECHER H,LAUTSCHAM V.From Ruin to Bankruptcy for compound Poisson surplus processes[J].Astin Bulletin,2013,43(2):213-243.
[4] GERBER H U,YANG H,SHIU E S W.The Omega model:from bankruptcy to occupation time in the red[J].European Actuarial Journal,2012,2(2):258-272.
[5] ALBRECHER H,GERBER H U,SHIU E S W.The optimal dividend barrier in the Gamma-Omega model[J].European Actuarial Journal,2011,1(1):43-55.
[6] WANG Xiu-lian,WANG Wei,ZHANG Chun-sheng.Ornstein-Uhlenback type Omega model[J].Frontiers of Mathematics in Chain,2016,11(3):737-751.
[7] 郑灿亮.马氏环境下一类风险模型的破产概率[D].北京:清华大学,2010.
[8] JASIULEWICZ H.Probability of ruin with variable premium rate in a Markovian environment[J].Insurance Mathematics and Economics,2001,29(2):291-296.
[9] LU Yi,LI Shuan-ming.On the probability of ruin in a Markov-modulated risk model[J].Insurance Mathematics and Economics,2005,37(3):522-532.
[10] ALBRECHE H,CHEUNG E C K, THONHAUSER S.Randomized observation periods for the compound Poisson risk model:dividends[J].Astin Bulletin,2011,41(2):645-672.
[责任编辑:张存凤]
Expected discounted penalty function for a class of Omega models
ZHOU Ying, WANG Xiu-lian
(College of Mathematical Science, Tianjin Normal University, Tianjin 300387, China)
On the basis of the classical risk model, this paper considers the expected discounted penalty function according to the company’s surplus plus or minus charge the premium. Firstly, we obtain the integral differential equation for the expected discounted penalty function of bankruptcy by the law of total probability. Secondly, the differential equation for the expected discounted penalty function in the case of exponential claim is given. Finally, choosing three common bankruptcy rate functions in the penalty function as exponential function, we have derived the explicit expressions of the expected discounted penalty function by changing differential equation to Kummer function.
Omega model; bankruptcy rate function; discounted penalty function; Kummer equation
1673-2944(2016)06-0072-08
2016-07-06
2016-09-27
国家自然科学基金资助项目(11401436);天津师范大学博士基金资助项目(52XB1204)
周颖(1991—),女,安徽省无为县人,天津师范大学硕士研究生,主要研究方向为随机过程在金融保险中的应用;[通信作者]王秀莲(1965—),女,山西省吕梁市人,天津师范大学副教授,硕士生导师,主要研究方向为随机过程在金融保险中的应用。
O211.67
A
