刘　牮，李　彧

(上海理工大学 光电信息与计算机工程学院,上海200093)



一种用于信号估计的改进变步长LMS算法

刘牮，李彧

(上海理工大学 光电信息与计算机工程学院,上海200093)

为了改善现有的变步长LMS自适应算法在对带有噪声的信号估计中存在步长调节参数较多、收敛速度慢、不易调节、对噪声较为敏感等现象，综合已有的变步长算法提出了一种基于升余弦窗函数与误差延时相结合的可调节的变步长算法，给出理论分析的同时利用MATLAB建模仿真验证，表明该算法能进一步提高收敛速度的同时，确保在低信噪比环境下能顺利提取期望信号。经过改进的升余弦窗函数可以做到仅调节一个参数即可完成信号估计，验证的结果表明，该算法在收敛速度与稳态失调上均优于其他变步长算法，具有一定的工程实用价值。

LMS算法；自适应信号估计；变步长；收敛速度；MATLAB

0　引言

信号采样估计系统中由于引入噪声导致所估计的结果包含较大的误差。由于噪声属于随机信号，呈现为分布在全频段内的随机信号，这导致了传统意义上的FIR或其他数字滤波方法，针对特定频率段信号滤除的功能在对于白噪声的滤除上无法达到满意效果。自适应滤波算法可以利用输入信号与滤波器输出信号的差值作为反馈来不断调整滤波器的系数，从而达到理想的滤除噪声效果。

随着自适应概念的提出，LMS(Least Mean Square)算法在自适应滤波方面由于工程实现简单，收敛速度理想，广泛应用在信号估计、噪声滤除、系统辨识等领域。自适应算法中收敛速度、稳态失调量、跟踪速度、稳态误差是衡量算法优劣的判别因素，其中收敛速度与稳态失调量是最关键的两个因素。传统LMS算法中收敛步长为固定值，一般是比较小的数，当步长较大时收敛速度较快，能很快地使误差收敛在一个稳定震荡的范围内，这个误差无法消除[1-2]。当选择较小的步长时虽然可以使误差缩小但导致收敛时间大大增加[3]。为了解决这一矛盾，许多改进的算法被提出[4-10]，这些算法基本遵循一个规则，当系统初始工作时误差较大，应当使用较大的步长因子，随着时间的增加，系统反馈的误差逐渐缩小时步长随之变小，降低系统的收敛速度，进一步减小系统输出误差。比较有代表性的变步长是文献[6-9]提出的基于非线性算法的步长调整。文献[3]29提出利用sigmoid函数修改步长，但随着误差的缩小，该函数在零误差附近步长变化较为剧烈，容易导致系统输出震荡，影响算法精度。文献[9]654提出的基于指数函数的变步长大大改进了收敛速度，但在噪声干扰的情况下，多次误差反馈后噪声信号仍然保持相关性，对噪声滤除的效果并不理想。文献[6,8]95，98针对此现象引入了延迟因子，较好地修正了噪声对信号估计的影响，但由于引入了较大的延时使其收敛速度有所降低。文献[7,10]1824,2336提出的改进算法兼顾了较快的收敛速度与保持低信噪比下较小的稳态误差，但引入的步长函数所涉及的参数较多，给系统的调试带来了不便。

综上所述，本文在现有的步长调整原则下，提出了一种基于升余弦窗函数的步长调整算法。该算法能改善sigmoid函数收敛速度的同时，同样能满足低信噪比下对包含噪声的信号的估计，同时减少了调整参数，更加便于工程实践。

1　LMS信号估计的原理及其改进

1.1LMS算法原理分析

引入带噪声信号估计的模型，该模型图如图1所示。

图1　LMS算法估计带噪信号模型图

该模型中S为待估计信号，N为噪声，D为延时单元，FIR为自适应滤波器，O为输出，输出为期望信号中包含的噪声的最优估计，实际上是对期望信号中的噪声做最优估计，误差e(n)对FIR滤波器的系数进行自动调节。将输入的信号(期望信号与噪声的叠加)减去输出即可得到所估计的不含噪声的信号。

LMS算法是基于递推梯度下降的方法，寻找误差最小化的最优方程解，从而得出FIR滤波器各阶系数，其迭代公式如下：

(1)

(2)

(3)

式中：W是滤波器的权系数向量，通常滤波器选择FIR型滤波器，因为FIR滤波器为稳定系统，并且可以保证线性相位。e(n)是误差，用于反馈调节滤波器系数；d(n)是期望信号，用于和滤波器输出做差；μ就是步长因子，LMS算法要求μ的取值为：

(4)

该处Px为：

(5)

式中：N为采样点数；M为滤波器阶数。由式(1)和式(2)得：

(6)

式中：e(n)是与输入信号有关的误差。该误差在图1所示的系统中代表了对噪声的估计。将理想d(n)表示为[11]：

(7)

式中：W*为理想滤波器系数；e*为理想估计下的噪声信号。假设：

(8)

表示滤波器真实系数与理想系数的偏差，式(7)减去式(6)，再对e(n)求平方得：

(9)

当引入e(n)e(n-1)[6]96作为步长调节因子时：

(10)

由于延时后导致X(n)和e*(n)不相关[12]，则对式(10)两边取期望得：

(11)

由于输入噪声为随机白噪声，对于延迟一个单位的白噪声来说，已经变为不相关信号，所以在使用e(n)e(n-1)代入计算步长因子时，已经可以起到噪声抑制的作用，从而估计出原始信号[8]98。

由上述分析可以得知，为了在有噪声环境下提取希望信号，必须加入一定的延时，针对白噪声的情况下，施加一个单位延时即可。

1.2LMS算法改进

基于文献[3]28所提出的步长因子变化准则以及之前所分析的引入一定延时的误差乘积作为步长因子调整的输入参数[13-14]，现提出基于升余弦窗的步长变化函数：

(12)

升余弦窗函数是为了减小采样序列中频谱泄露而引入的截断采样序列的函数，是一种边缘滚降平缓，并且具有比指数函数更加陡峭的衰减特性。该特性可以满足步长因子变化的准则，分析式(12)随着参数的变化，当α取0.7，β分别取不同的值时μ(n)的变化。

图2为β分别取512、256、128、64时的升余弦窗函数的波形图，在MATLAB中绘图时将迭代次数设置为64次。

图2　α=0.7 时不同β下的步长变化曲线

从图2中可以看出，在迭代次数不变的情况下，β的值可以调节曲线的衰减程度，当迭代次数固定，β值增大时，曲线衰减程度降低，如果β远远大于迭代次数时，在迭代次数范围内观察步长曲线时有可能会导致迭代完毕后仍然无法使e(n)收敛，造成算法失调。当迭代次数固定，β值逐渐减小时，可以观察出步长因子曲线衰减程度逐渐增加，当β减小至于迭代点数相同时呈现标准升余弦窗函数图形，该β值为临界值，如果继续减小β，则可能导致在步长因子调整的过程中违背其变化准则，出现大幅度震荡或不收敛的情况。β的取值推导过程如下，对滤波器权系数公式(3)两边取数学期望得：

(13)

式中：W*为滤波器最佳系数的维纳解；R为输入信号的自相关矩阵E[X(n)XT(n)]。对于该矩阵可以转换为对角矩阵与其正交特征向量的乘积，为了使得LMS算法收敛，μ的值应该满足如下条件

(14)

(15)

此处，K为迭代次数，当满足以上条件时，调节β值可获得较满意的收敛速度。

针对β值不变的情况，不同的α值会对步长因子曲线带来影响，选取迭代次数为64次，当β取128时，不同的α对步长因子曲线的影响如图3。

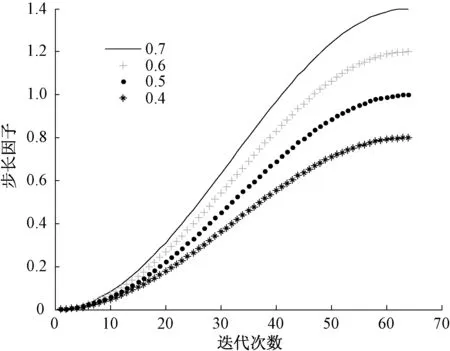
图3　β=128 时不同的α下步长变化曲线

从图3中可以看出，当α为0.7时，具有最大衰减程度的步长变化曲线，图3中的4条曲线均满足步长因子变化趋势，随着迭代次数的增多，误差逐渐缩小趋向于零。α=0.7时，此时误差最大，表示具有1.4的误差，由于在含噪声信号的估计中多次迭代的误差均为比较小的数，因此选定一个合适的α值后一般不需要再次调整，在本文所提到的信号估计系统中，多次迭代的误差均小于1。为稳妥起见，可将该值设为0.7，如在实际测试过程中发现无法收敛时，调节该参数。

经过以上分析可以发现α和β都能起到调节步长因子的作用，相对于α来讲，β的调节范围更广，可以理解为β属于粗调整，α属于细微调整，系统初次调试时可以将α设置为稍大一些的值，在带噪信号估计的工程实践中甚至可以固定使α=0.7，仅调节β即可获得满意的收敛效果。

2　算法对比

为对比本文算法与其他算法在收敛速度与均方误差上的性能，在MATLAB下设计程序，输入信号为零均值，方差为1的高斯白噪声，此处仅仅测试对于输入高斯白噪声，输出跟随输入未知系统时的收敛速度与均方误差，本次测试使用未知系统加权系数为[0.8，0.3]，迭代次数为2 000次，如图4～7所示。针对之前分析，同时给出了不同α与β值的步长曲线与均方误差值来验证之前的分析。从图4到图7中可以看出，α较大，β值较小的时候，此时升余弦窗的滚降趋势增大，LMS算法趋向于更快的收敛速度，更迅速地收敛于均方误差最小值。快速收敛的同时为了减小稳态失调，步长因子开始变化趋缓满足之前所讨论的收敛原则。

图4　α=0.7，β=20本文算法 2 000次迭代的步长因子曲线

以下为对比文献的算法曲线。图8，图9为文献[3]29的不延时计算误差算法的步长曲线与均方误差曲线。图10、图11为文献[8]98的有延时计算误差算法的步长曲线与均方误差曲线。从图8至图11可以看出，具有延时的误差所导出的步长能更快速收敛的同时，对于噪声的剔除更理想，亦即对噪声更不敏感，其步长因子在多次迭代后相比于无延时误差的步长逐渐趋于稳定。而本文的算法能综合两者的优点，快速收敛的同时具有更小的稳态失调量。

图5　α=0.7，β=20本文算法 2 000次迭代均方误差曲线

图6　α=0.1，β=32本文算法2 000次迭代的步长因子曲线

图7　α=0.1，β=32本文算法 2，000次迭代均方误差曲线

图8　2 000次迭代误差不延时算法的步长曲线

图9　2 000次迭代误差不延时算法的均方误差曲线

图10　2 000次迭代误差延时一个单位算法的步长曲线

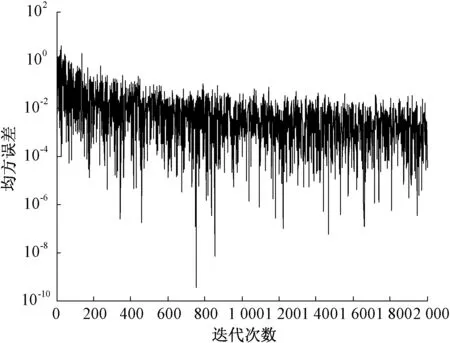
图11　2 000次迭代误差延时一个单位算法的均方误差曲线

3　算法应用于带噪信号估计的计算机仿真

在MATLAB下创建纯净正弦信号，s=sin(2πt/10)，叠加高斯白噪声，信噪比为10(低信噪比)，延迟单元D设为延迟100，滤波器选用FIR，32阶加权系数，输入为受噪声污染的正弦信号，输出为降噪后的估计信号，经由MATLAB按照图1模型，并使用升余弦窗函数作为步长调节函数，α=0.7，β=14，仿真程序运行结果如图12。

图12(a)表示在MATLAB下仿真出的叠加了污染信号(高斯白噪声)的波形；图12(b)表示所叠加的污染信号，均值为零，方差为1的高斯白噪声信号；图12(c)表示未叠加高斯白噪声的正弦信号；图12(d)表示通过LMS降噪模型(图1)后输出的正弦信号，可以明显地观察到噪声信号已经被有效抑制；图12(e)表示使用升余弦窗变步长算法的均方误差(学习)曲线。通过图中实际滤波信号与带噪信号的对比，可以明显看出噪声信号被极大地抑制，证明通过升余弦窗调节的可变步长LMS算法能够满足带噪信号的估计。

4　结论

针对不同变步长调节方法，综合考虑后引入一种方便可行，参数较少的变步长函数，在保证能将低信噪比的信号较好地提取出来的同时进一步加快收敛速度，同时简化参数，本文中的算法可以较快地调整出满意的效果，大多情况下根据实际情况仅仅调节一个β值即可满足要求，而且可以利用在DSP平台上的数字滤波窗函数[15]，节省硬件资源，操作简便，具有较广阔的应用前景。

图12　整体滤波效果图

[1]曹景升, 单毅, 樊雪涛. 自适应滤波器在噪声处理中的应用[J]. 电子技术与软件工程, 2015(7):129.

[2]郑顾平, 杜向楠. 基于LMS自适应滤波的零序电流去噪研究与实现[J]. 电力科学与工程, 2011, 27(12):27-31.

[3]陈泳, 田金鹏, 刘燕平. 一种新的变步长LMS自适应滤波算法[J]. 电子测量技术, 2015, 38(4):27-31.

[4]王洪诚, 王蕾, 沈霞,等. 基于改进增益型自适应LMS算法的谐波检测方法[J]. 电力系统保护与控制, 2016, 44(5):42-46.

[5]张炳婷, 赵建平, 刘凤霞. 一种改进的可变步长LMS算法及性能分析[J]. 通信技术, 2015, 48(11):1217-1221.

[6]还秋云, 邱晓晖, 刘晓飞. 引用范数的双曲正切函数变步长LMS算法[J]. 信号处理, 2014, 30(1):93-99.

[7]张红梅, 韩万刚. 一种新的变步长LMS自适应滤波算法研究及其应用[J]. 仪器仪表学报, 2015, 36(8):1822-1830.

[8]李梁, 庹先国, 李怀良,等. 一种改进的自适应滤波算法在微震信号处理中的实现[J]. 中国测试, 2015, 41(1):97-99,119.

[9]张炳婷, 赵建平, 马淑丽. 新的变步长LMS算法在系统辨识中的应用[J]. 通信技术, 2015, 48(6):653-656.

[10]郭瑞, 李宝华, 马奥运. 一种基于改进双曲正切函数的变步长自适应滤波算法[J]. 计算机应用研究, 2015, 32(8):2335-2338.

[11]陈立伟, 谭志良, 崔立东. 改进的LMS算法在噪声对消中的应用[J]. 无线电工程, 2015(6):70-73.

[12]英格尔. 数字信号处理 (MATLAB版)[M]. 西安:西安交通大学出版社, 2008.

[13]张红梅, 韩万刚. FIR滤波器时延分析及其在信号融合中的应用[J]. 武汉大学学报(工学版), 2016,49(2):303-308.

[14]董胡. 基于窗函数与MATLAB的数字FIR滤波器设计[J]. 微型电脑应用, 2016(3):30-32.

[15]郭璐, 黄鹤, 杜凯,等. DSP环境下新的变步长LMS自适应滤波算法[J]. 电子设计工程, 2016(1):135-137.

An Improved Variable Step Size LMS Algorithm for Signal Eestimation

LIU Jian, LI Yu

(School of Optical-electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China )

In order to improve the performance of the existing variable step-size LMS algorithm during signal estimation with the problems such as too many parameters, rather slow convergence speed, relatively difficult to adjust, and quite sensitive to noise, a new variable step-size algorithm combining raised cosine windows function and delay error was proposed based on the existing one. The theoretical analysis and the simulation in MATLAB are given in this paper. The proposed algorithm can not only improve the convergence speed but also ensure the desired signal be extracted successfully in low SNR environment. The improved raised cosine windows function can help LMS algorithm estimate the signal with only one parameter, and the results show that the algorithm is superior to other variable step-size algorithms in both convergence speed and steady state, and it also is of certain engineering and practical value.

LMS algorithm; adaptive signal estimation; variable step-size; convergence speed; MATLAB

2016-06-04。

上海市科技英才扬帆计划项目(15YF1408300)。

刘牮(1961-)，男，副教授，主要研究方向为电子技术及嵌入式技术应用，E-mail：liuliu2702@163.com。

TN911.7； TH701

ADOI:10.3969/j.issn.1672-0792.2016.10.004