寸得偶，晏　林

（文山学院 数学学院，云南 文山 663099）

积分因子求法探讨

寸得偶，晏林

（文山学院 数学学院，云南 文山 663099）

积分因子法是求解微分方程通解的重要方法之一，且用积分因子法求解恰当方程是整个常微分方程教学的基础。探讨求解积分因子的四种方法：凑微分法、观察法、公式法、分组法，分析认为凑微分法、观察法、公式法对简单的微分方程求解更简单，更清晰，而分组法对于复杂的微分方程求解显得更实用。同时，对积分因子在特殊方程中的应用进行讨论，分析认为凡是可分离变量方程和可化为可分离变量的方程，线性方程和可化为线性方程的方程，都可以用积分因子法去求解。

积分因子；微分方程；求解方法

积分因子的引入是为解决非恰当微分方程化为恰当微分方程求通解的过渡桥梁，积分因子的求法传承了偏导数在方程中的运用，有助于加深了学生对积分的深刻理解，积分因子的出现为微分方程的求解结果创造了条件。积分因子已从简单的求解非恰当方程过渡到求解复杂的高阶微分方程中，并且规律也越来越多，应用方面更是推广到各个领域，对其求法的探讨也越来越深入。但对积分因子求法的具体归纳总结却是不全面的，由此本人将首先对积分因子的求解方法进行归纳，并总结出适用的微分方程，也会提出一些对应方法的求解步骤，本人也想对一些有规律性的积分因子进行证明。同时，对积分因子的一些常见应用也在这里进行一些讨论。

1　积分因子的性质

1.1积分因子的概念

若对对称形式的方程

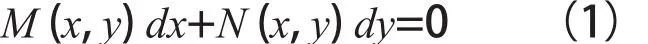
存在一个连续函数μ = μ(x,y)≠0，使得方程μ(x,y) M (x,y) dx+μ(x,y)N(x,y)dy=0成为一个恰当微分方程，即存在二元函数v，使μMdx+μNdy≡dv，则称μ(x,y)为M (x,y) dx+N(x,y)dy=0的积分因子[1]。这时v(x,y)=C就是方程（1）的通解，因此可见，解决问题的关键是设法求出积分因子。

1.2积分因子的充要条件

积分因子的形式多样，以至于积分因子存在的充要条件各不相同，本文只讨论一些简单基础性较强的积分因子的充要条件。

引理1函数μ(x,y)为方程M (x,y) dx+N(x,y)dy=0积分因子的充要条件

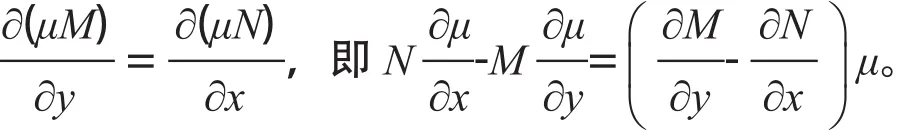
结论1方程M (x,y) dx+N(x,y)dy=0有只与x有关的积分因子的充要条件是，这里φ(x)为x的函数，且积分因子为μ=e∫φ(x)dy。

结论2方程M (x,y) dx+N(x,y)dy=0有只与y有关的积分因子的充要条件是，这里ψ(y)为y的函数，且积分因子为μ=e∫ψ(x)dy。

1.3积分因子不唯一性

若μ(x,y)是（1）式的积分因子，u(x,y)是方程M (x,y) dx+N(x,y)dy=0相应于μ(x,y)的恰当函数，则对任意非零连续函数φ(u)，μφ(u)亦是M (x,y)dx+N(x,y)dy=0的积分因子。例如：ydx-xdy=0有不同的积分因子。这说明了积分因子存在，但不唯一。由此，在具体解题过程中，由于求出的积分因子不同导致求出的通解具有不同的形式。

2　积分因子的求法

求解积分因子相当于求解一个偏微分方程，计算偏微分的方法也是求解积分因子必备的知识基础。下面介绍一些求解积分因子的方法：

2.1凑微分法

凑微分法是求解积分因子的基础，它主要应用于一些简单的微分方程中。在运用这种方法前，应熟练掌握一些基本的二元函数的全微分。

例1求解方程ydx- (x2+y2) dx-xdy=0。

解先将方程移项得ydx-xdy=(x2+y2) dx；由凑微分法中可得到方程的积分因子为，将μ(x,y)乘于方程左右两端得积分之后得所求方程通解：

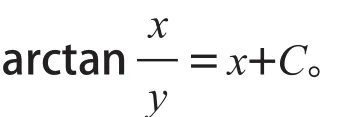
综上，凑微分法解决微分方程的步骤：首先考虑方程是否需要移项、通分、同类合并等；其次考虑是否可以构造基本的二元函数的全微分；再次是在凑微分过程中找到积分因子；最后就是积分求出方程的通解。

2.2观察法

观察法求解积分因子的过程时，除了要能牢记凑微分法中的基本二元函数的全微分，还要熟练掌握恰当微分方程中的“分项组合”方法，只有这样才便于运用观察法来求解积分因子。

2.2.1运用基本二元函数的全微分观察

若在非恰当微分方程中可以直接观察到含有基本二元函数的全微分公式的某一部分，我们就可以尝试凑出所需的另一部分。在这一过程中要注意积分因子的不唯一，如在中的ydx-xdy就有5种不同形式的积分因子这5种积分因子并不是所有的都是满足方程的积分因子，你需要观察方程的另一部分，从而得到适合方程的积分因子为，再按照积分因子概念中μ(x,y)M (x,y) dx+μ(x,y)N(x,y)dy=0的方法求解方程。

2.2.2分项组合后观察

对于某些简单的微分方程不能直接观察出它的积分因子时，可以尝试着先分项组合，再观察方程得到积分因子，最后求解。

例2求(ex+3y2)dx+2xydy=0积分因子及通解。

解先分项组合：exdx+(3y2dx+2xydy)=0（2）

由3y2dx+2xydy观察可得，给其乘一个x2就有d(x3y2)=3x2y2dy+2x3ydy成立，从而可得方程积分因子μ(x,y)=x2；将积分因子乘以（2）式的两端，即：x2exdy+d(x3y2)=0，再用分部积分法：∫udv=uv-∫udu求得原方程的通解为exx2-2xex+2ex+x3y2=C。

2.2.3观察方程中含积分因子(xy)-n

在有形如ydx+xdy 的式子中积分因子是(xy)-n，带入方程后便得到全微分方程是计算中应注意，积分因子中的(xy)-n的n次方选取的是x或y中的最高次方且n≥2。

例3求ydx+(x-3x3y2)dy=0的积分因子和通解。

解先将方程组合让其出现ydx+xdy的式子，即：

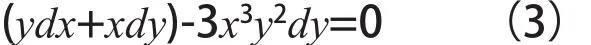
又因-3x3y2中可以知道x的最高次方为3，所以积分因子中n=3，则乘以（3）式的左右两端的dy=0，即再两边积分得方程的通解

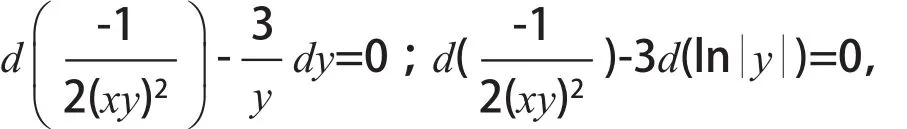
综上，观察法是在熟练做题后积累经验和总结方法的基础上，才能取得有效快捷的解题方法，对于初学者和题量做得少的学者，这种方法难度系数较高，而且观察法的要求较高，需要有牢固的知识基础。

2.3公式法

运用公式法求解积分因子体现了微分方程的一种可循规律，在积分因子存在的充要条件中已经提到只有x或y的两种积分因子的公式，分别是结论1和结论2。下面给出其他形式的积分因子形式：

2.3.1具有μ(x,y)形式的积分因子

方程M (x,y) dx+N(x,y)dy=0有形如μ(x±y)积分因子[2]的充要条件为则积分因子

例4求方程(2x3+3x2y+y2-y3-3)dx+(2y3+3xy2+x2-x3-3)dx=0的积分因子。

2.3.2具有μ (xα+yβ)形式的积分因子

方程M (x,y)dx + N (x,y)dy = 0具有形如μ= μ (xα+yβ)的积分因子满足的充要条件[3]为f (xα+yβ)且积分因子为

注α,β的选取是由x，y的最高次方决定的。

假设μ(xα+yβ)为方程M(x,y)dx+N(x,y)dy=0的积分因子，由积分因子充要条件结合上述的（4）式和（5）式进行相应替换就可以得到这样的连等式子在将式子首尾连成等式化简就可得然而要上式满足条件当且仅当= f (xα+yβ)时，可求解出积分因子μ=e∫ f (x α+y β ) d (x α+y β )。

例5求方程ydx-(x2+y2+x)dy=0的积分因子。

解由已知M=y；N=-(x2+y2+x) ；则有由上充要条件可以代入公式求得方程的积分因子 ：μ=e∫ f (x2+y 2) d (x2+y 2)

然而，我们在做题时还要注意假设方程具有μ=μ (xα-yβ)形式的积分因子时满足的充要条件为时是有一点点微妙的变化的，那它的积分因子公式应为：μ=e∫ f (x α-y β ) d (x α-y β )。它在常微分方程中属于较为复杂的类型，它的证明方法与μ=μ (xα+yβ)类似。

公式法求解积分因子局限性较大，它要在满足一定的充要条件下求解会使整个求解过程显得简易。对于一些只关于x或y的非恰当微分方程，带公式求积分因子再求解方程的通解会显得直观简便。然而对于一些特殊的积分因子求解公式，需要明确方程相应的积分因子形式，这就要求在解题过程中需要进行一定的尝试判定具有的积分因子的形式。公式法对于初学者计算非恰当微分方程通解来说较为容易掌握，它只要记得一定的充要条件和计算公式，将相应的值代入就能解决问题。

3.4分组法

分组法求解积分因子是对较为复杂的微分方程所采取的一种有效解决问题的方法，它基于用凑微分法、观察法、公式法都不易求出积分因子的情况下所选择的方法，分组法也是一种运用分组思想找积分因子进而求解的方法。

对于一般形如M(x,y)dx+N(x,y)dy=0的复杂方程，若能将它的左端分成几组进行考虑，比如将M(x,y)dx+N(x,y)dy=0式分成如下两组：

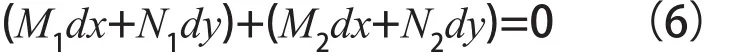
然后，运用公式法求这两组积分因子：

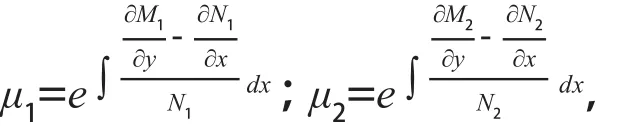
以及相对应的恰当函数方程分别为：

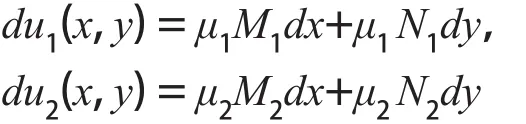
由此借助 μ1、 μ2、 u1、u2便可求得整个方程。

注：在求u1和u2时积分过程采用的是定积分，这就要注意选择x，y的积分途径。

事实上，对于任意非零连续函数φ(u1)和ψ(u1)，μ1φ(u1)和μ2ψ(u2)都分别是（6）式的第一组和第二组的积分因子。由于φ、ψ有广泛选择的可能性，因此我们能选择φ、ψ，使其满足μ=μ1φ(u1)=μ2ψ(u2)，则μ既是方程（3～6）的第一组积分因子又是（6）式的第二组积分因子，因而可以总结为μ就是整个方程M(x,y)dx+N(x,y)dy=0的积分因子[4]。

例6试用分组法求解方程(4xy+3y4)dx+(2x2+5xy3)dy =0的积分因子和通解。

解 先将方程分组后为(4xydx+2x2dy)+(3y4dx+ 5xy3dy)=0，由此可知方程前一组为(4xydx+2x2dy)，即M1=4xy；N1=2x2，后一组为(3y4dx+5xy3dy)，即M2=3y4；N2=5xy3；再运用公式求出前一组的积分因子为：

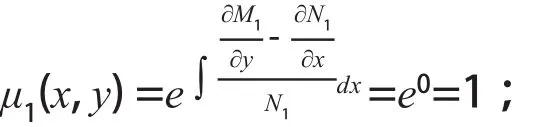
则其恰当函数为

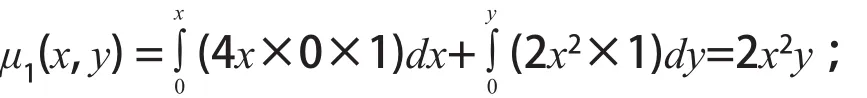
而对于后一组的积分因子：

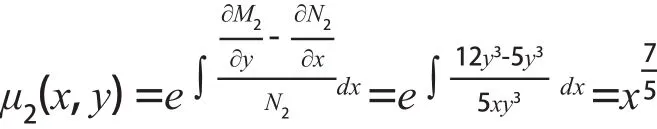
则相对应的恰当函数为：

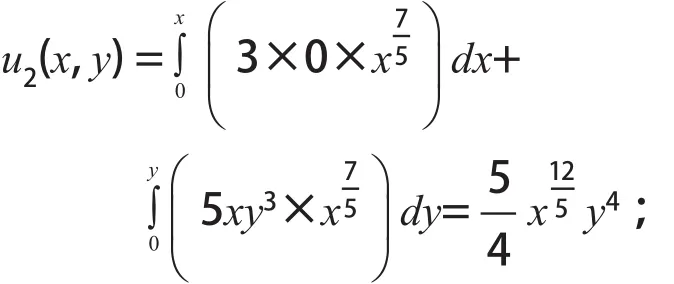
故当x2y≠0时，原方程的积分因子为：μ1φ(u1) = μ2ψ(u2)=μ=x2y；再将积分因子乘与方程的两端：x2y(4xydx+2x2dy)+x2y(3y4dx+5xy3dy)=0，将其化简后进行观察可得：2x2yd(x2y)+d(x3y5)=0，最后将其两边进行积分得到方程的通解：(x2y)2+x3y5=C。当x2y=0时，原方程仍然成立，故y=0亦是原方程的解。

综上，原方程的通解为(x2y)2+x3y5=C（C为任意常数）。由上述讨论及本例可知：一般来说运用分组积分因子法求解比较复杂的对称形式方程时，有两个问题应着重解决：其一，关键在于较复杂的对称形式的方程进行适当的分组，使各组的积分因子与相应的恰当方程都易于求解得出来。其二，重难点在于适当的选取φ(u1)和ψ(u2)，在选取中要与u1和u2建立联系，并尽可能的去掉常系数，还要满足μ1φ(u1)=μ2ψ(u2)。

分组法是使微分方程求解中出现两个及两个以上的积分因子，对其积分因子寻求满足条件达到求解的过程。这种方法是以凑微分法、观察法、公式法为基础来深层次的解决复杂的微分方程通解的过程，同时，这种方法可以提高解题的综合能力和培养学生全面思考问题的能力。

3　积分因子的应用

随着对恒等式微分方程的结果的需求，积分因子从解决非恰当微分方程逐步应用到一些常见类型的一阶微分方程的求解过程中，如：可分离变量方程、线性方程、齐次方程。

3.1用积分因子解可分离变量方程

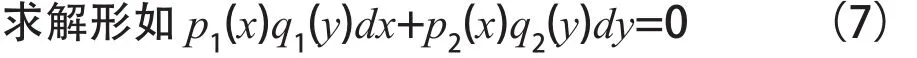
的分离变量的积分因子可以运用观察法求解，若让（7）式的两端同时乘以这样一个式子可以得到由此可以从中知道M由此可知；由此可以确定原方程的积分因子为

例7求方程(xy-y)dx+(xy-x+y-1)dy=0的积分因子与通解。

解先将方程变形为y(x-1)dx+(x+1)(y-1)dy=0，可知这是一个分离变量方程，由此它的积分因子满足再将其乘于方程的两边就可以得到这样的的一个式子：将式子两边积分得到原方程的通解为：

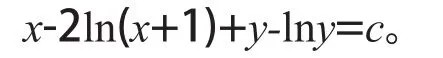
用积分因子解可分离变量方程是将积分因子运用到基础恰当微分方程的一种回归原本的思想，它只要将能分离变量的方程求解归于公式化，在求能分离变量的方程中只要找到积分因子所要的条件，再结合积分的思想，就可求出通解。从而可以运用这种方法来解决一些实际问题，如：细菌繁殖；储水槽的水位问题，它们都需列出分离变量方程并求出结果，来得到一定的规律。

3.2用积分因子解齐次方程

由齐次方程为[5]：P(x,y)dx+Q(x,y)dy=0，只有当满足xP+yQ≠0时，方程就有形如这样的积分因子：

证明首先我们不妨设P(x,y)，Q(x,y)是m次齐次函数，那么就有P(tx, ty)=tmP(x,y)；Q(tx, ty)=tmQ(x,y)；然后让上两式的两边对参数t求导并且取t=1，则有；那么在这时为了要证明是齐次方程的积分因子，只需要证明有这样的等式

例8求齐次方程2xydx-(x2+y2)dy=0的积分因子及通解。

解由方程是一个齐次方程那就可以得到；P=2xy，Q=-(x2+y2)则积分因子为：；在将积分因子乘以方程的两端得观察可得它是全微分方程，由此可改写为：故两端积分后得原方程通解：x2-y2=Cy。

综上，对于齐次方程求通解时，只要找到相应的P、Q就可以代公式求解积分因子，这种利用积分因子解决问题是高效的，便易的。

3.3用积分因子解线性方程

综上，只要是线性方程和可化为线性方程的方程，采取用积分因子求解的方法来求通解是比较容易的，因为只要能在方程中找到M(x,y)，N(x,y)在，再代相应积分因子求解公式就可求出方程的通解。

[1] 王高雄，周之铭.常微分方程[M].北京:高等教育出版社，1983：55-56.

[2] 李君士.积分因子的求法[J].九江师专学报（自然科学版），1989（2）：64-68.

[3] 李德新.两类特殊微分方程的积分因子解法[J].福建农林大学学院，2004（2）：269-271.

[4] 西南师范大学数学与财经学院编.常微分方程[M].重庆:西南师范大学出版社，2005：83-88.

[5] 袁荣.常微分方程[M].北京:高等教育出版社，2012：46-47.

[6] 叶彦谦.常微分方程讲义[M].北京:人民教育出版社，1979：47-48.

[7] 钱祥征，黄立宏.常微分方程[M].长沙:湖南大学出版社，2007：28-29.

A Study on Integral Factor Method

CUN Deou, YAN Lin
(School of Mathematics, Wenshan University, Wenshan Yunnan 663000, China)

Integral factor method is one of the most important methods for solving differential equations and it's the basis of the ordinary teaching of differential equation. The paper studies four methods of solving integral factor, which are improvising differentiation, observation, formula and grouping method. The fi rst three methods are more simple and clear, and the forth method is more practical. Meanwhile, the paper discusses the application of integral factor in special equation and deems that the integral factor method can be used in the equation of separation of variables, the equation which can be converted into the equation of separation of variables, linear equation and the equation which can be converted into linear equation.

integrating factor; differential equation; solving method

O177.6

A

1674 - 9200（2016）03 - 0107 - 06

（责任编辑刘常福）

2015 - 06 - 19

寸得偶，男，云南盈江人，文山学院数学学院2011级应用数学专业学生；晏林，男，云南富源人，文山学院数学学院教授，主要从事代数学和数学实验方面的研究。