张立卓

(对外经济贸易大学统计学院, 北京100029)



关于线性子空间基的一种求解方法

张立卓

(对外经济贸易大学统计学院, 北京100029)

讨论了线性子空间基的一种求解方法.

线性子空间； 基； 维数

众所周知，关于线性子空间基的求解方法要视具体情况而定，本文拟通过下述两例探讨求解线性子空间基的一种方法.

定义1设W是数域K上线性空间V的非空子集，如果对任意α,β∈W,k∈K，有

α+β∈W，且kα∈W，

则称W是V的一个线性子空间.

定义2设W是数域K上线性空间V的一个子空间，W中的向量组α1,α2,…,αr如果满足：

(i) α1,α2,…,αr线性无关；

(ii)W中每一向量都可由α1,α2,…,αr线性表示，则称α1,α2,…,αr是W的一个基.

定义3设W是数域K上线性空间V的一个子空间，W的一个基所含向量的个数称为W的维数，记作dimW.

定理1n阶矩阵A可对角化的充分必要条件是A有n个线性无关的特征向量.

定理2数域K上n阶矩阵A可对角化的充分必要条件是A的特征多项式的全部复根都属于K，并且A的每个特征值的几何重数(特征子空间的维数)等于其代数重数(特征值在特征多项式的根的重数)[1].

定理3如果B是主对角元两两不等的对角矩阵，那么与B可交换的矩阵一定是对角矩阵[2].

证设B=diag{b1,b2,…,bn}，其中b1,b2,…,bn两两不等，如果n阶矩阵A=(aij)与B可交换，即AB=BA，以AB(i;j)表示AB的第i行、第j列的元素，于是

AB(i;j)=BA(i;j)(i,j=1,2,…,n)，

即aijbj=biaij，也即aij(bj-bi)=0，又bj≠bi(i≠j)，因此aij=0(i,j=1,2,…,n,i≠j)，从而A=(aij)为对角矩阵.

定理4设V是数域K上一个线性空间，如果dimV=n，则V中任意n个线性无关的向量都是V的一个基.

例1设Mn(R)是实数域R上全体n阶矩阵按照通常的加法和数量乘法构成的实数域R上的线性空间

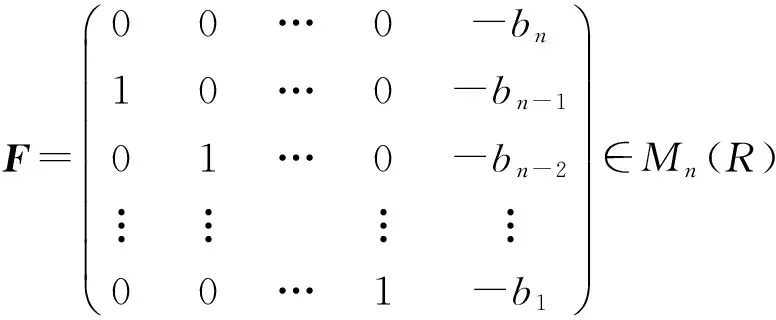
(i) 设A=(aij)∈Mn(R)，如果AF=FA，证明A=an1Fn-1+a(n-1)1Fn-2+…+a11E；

证(i) 设A的列向量组为α1,α2,…,αn，记A=(α1,α2,…,αn)，令

B=an1Fn-1+a(n-1)1Fn-2+…+a21F+a11E，

(1)

设B的列向量组为γ1,γ2,…,γn，记B=(γ1,γ2,…,γn)，下面要证B=A，只需证

γj=αj,j=1,2,…,n.

设ε1,ε2,…,εn为单位列向量组，注意到

Fε1=ε2,F2ε1=Fε2=ε3，…，Fn-1ε1=Fn-2ε2=…=Fεn-1=εn，

(2)

由(1)式和(2)式，有

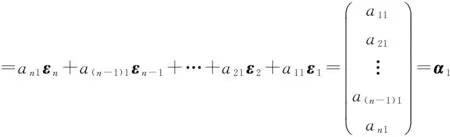
即γ1=α1，由上述证明知，Bε1=γ1=α1=Aε1，又由AF=FA可知

AF2=(AF)F=(FA)F=F(AF)=F(FA)=F2A，

类似地，A与Fn-1,Fn-2,…,F3均可交换，显然B与Fn-1,Fn-2,…,F,E均可交换，又由(2)式，有

γ2=Bε2=B(Fε1)=(FB)ε1=F(Bε1)=F(Aε1)=(FA)ε1=A(Fε1)=Aε2=α2，

γ3=Bε3=B(F2ε1)=(F2B)ε1=F2(Bε1)=F2(Aε1)=(F2A)ε1=A(F2ε1)=Aε3=α3，

…………………………………………………………

γn=Bεn=B(Fn-1ε1)=(Fn-1B)ε1=Fn-1(Bε1)=Fn-1(Aε1)=(Fn-1A)ε1=A(Fn-1ε1)

=Aεn=αn，

即A=(α1,α2,…,αn)=(γ1,γ2,…,γn)=B，从而由(1)式，有

A=an1Fn-1+a(n-1)1Fn-2+…+a21F+a11E.

(ii) 显然W⊂Mn(R)，且n阶单位矩阵E∈W，即W不是空集.任取X,Y∈W,∀k∈R，则XF=FX,YF=FY，于是

(X+Y)F=XF+YF=FX+FY=F(X+Y)，

即

X+Y∈W，

(kX)F=k(XF)=k(FX)=F(kX)，

即kX∈W，依定义1，W是Mn(R)的一个线性子空间.

显然Fn-1,Fn-2,…,E都在W中，由(i)可知，W中每一矩阵都可由Fn-1,Fn-2,…,E线性表示，下面要证Fn-1,Fn-2,…,E就是W的一个基，为此只需证Fn-1,Fn-2,…,E线性无关.

设k0E+k1F+…+kn-2Fn-2+kn-1Fn-1=O，等式两端右乘ε1，

k0ε1+k1Fε1+…+kn-2Fn-2ε1+kn-1Fn-1ε1=0，

由(2)式，即

k0ε1+k1ε2+…+kn-2εn-1+kn-1εn=0，

因ε1,ε2,…,εn-1,εn线性无关，所以

k0=k1=…=kn-2=kn-1=0，

即Fn-1,Fn-2,…,F,E线性无关，依定义2和定义3，Fn-1,Fn-2,…,F,E是子空间W的一个基，且

dimW=n.

注要求解W的一个基，可先证明

A=an1Fn-1+a(n-1)1Fn-2+…+a11E，∀A∈W，

为此令

B=an1Fn-1+…+a11E，

需证A的各列α1,α2,…,αn与B的各列γ1,γ2,…,γn对应相等，先证γ1=α1，即

Bε1=γ1=(a11,a21,…,a(n-1)1,an1)T=α1=Aε1，

再依A,B都与Fn-1,Fn-2,…,F,E可交换，有

αj=Aεj=AFj-1ε1=BFj-1ε1=Bεj=γj(j=2,…,n)，

即A=B.依F的结构特征，由(2)式

k0ε1+k1Fε1+…+kn-2Fn-2ε1+kn-1Fn-1ε1=0

⟺k0ε1+k1ε2+…+kn-2εn-1+kn-1εn=0，

因此Fn-1,Fn-2,…,F,E线性无关，是W的一个基.

评实数域上所有与F可交换的矩阵集合构成Mn(R)的一个子空间，而其一个基就是

Fn-1,Fn-2,…,F,E.

例2设

证显然W⊂Mn(R)，与上例(ii)同法可证，W是Mn(R)的一个线性子空间.由题设，A有n个线性无关的特征向量，依定理1，A可对角化，依定理2，A的特征值都是实数，且每个特征值的几何重数都等于其代数重数.设λ是A的一个特征值，此时矩阵λE-A有一个n-1阶非零子式

令

则A=PΛP-1，对∀X∈W，XA=AX，依上式

XA=AX ⟺ X(PΛP-1)=(PΛP-1)X.

⟺ (P-1XP)Λ=Λ(P-1XP)(上式两端分别左乘P-1和右乘P)

⟺ P-1XP=diag{d1,d2,…,dn}(定理3)

⟺ X=Pdiag{d1,d2,…,dn}P-1

⟺ X=P(d1E11+d2E22+…+dnEnn)P-1

⟺ X=d1PE11P-1+d2PE22P-1+…+dnPEnnP-1，

(3)

其中Ejj∈Mn(R) (j=1,2,…,n)，其元(j;j)=1，其余元素均为零. (3)式表明，∀X∈W，X都可由PE11P-1,PE22P-1,…,PEnnP-1线性表示，下面要证PE11P-1,PE22P-1,…,PEnnP-1就是W的一个基.首先，PEjjP-1∈W,j=1,2,…,n.这是因为

EjjP-1AP=EjjΛ=λjEjj=ΛEjj=P-1APEjj，

上式两端分别左乘P和右乘P-1，有

PEjjP-1A=APEjjP-1，

所以

PEjjP-1∈W,j=1,2,…,n.

其次，设k1PE11P-1+k2PE22P-1+…+knPEnnP-1=O，即

P(k1E11+k2E22+…+knEnn)P-1=O，

上式两端分别左乘P-1和右乘P，有

k1E11+k2E22+…+knEnn=O，

即

k1=k2=…=kn=0，因此PE11P-1,PE22P-1,…,PEnnP-1线性无关，依定义2和定义3，PE11P-1,PE22P-1,…,PEnnP-1就是W的一个基，且dimW=n.

又设αj(j=1,2,…,n)是A的属于特征值λj(j=1,2,…,n)的特征向量，则

显然E,A,A2,…,An-1∈W，设

l0E+l1A+l2A2+…+ln-1An-1=O，

用αj(j=1,2,…,n)右乘上式两端

l0Eαj+l1Aαj+l2A2αj+…+ln-1An-1αj=0，

即

因为特征值λ1,λ2,…,λn两两不等，依范德蒙行列式结论，

因此方程组只有零解，从而l0=l1=l2=…=ln-1=0，E,A,A2,…,An-1线性无关，因为dimW=n，依定理4，E,A,A2,…,An-1也是W的一个基.

注要证E,A,A2,…,An-1是W的一个基，可先求解W的一个基.由A可对角化，即存在可逆矩阵P，使P-1AP=Λ，从而PE11P-1,PE22P-1,…,PEnnP-1是W的一个基，于是dimW=n.依A的结构特征，再证A的n个特征值两两不等，因此E,A,A2,…,An-1线性无关，从而E,A,A2,…,An-1也是W的一个基.

评实数域上所有与A可交换的矩阵集合构成Mn(R)的一个子空间，而其一个基就是

E,A,A2,…,An-1.

[1]丘维声. 高等代数学习指导书(上册).[M].2版. 北京: 清华大学出版社, 2005: 333-334.

[2]丘维声. 高等代数学习指导书(上册).[M].2版. 北京: 清华大学出版社, 2005: 169-170.

A Method of Determining the Base of Linear Subspace

ZHANG Li-zhuo

(School of Statistics, University of International Business and Economics, Beijing 100029, China)

A method for determining the base of linear subspace is discussed.

linear subspace; base; dimensionality

2015-04-18；[修改日期]2016-03-30

张立卓(1963-),女，硕士，副教授，从事大学数学教学研究.Email:zlizhuo@uibe.edu.cn

O151.2

C

1672-1454(2016)04-0107-05