黄永忠，　刘继成

(华中科技大学数学与统计学院，武汉430074)



多元向量函数的中值定理及应用

黄永忠，刘继成

(华中科技大学数学与统计学院，武汉430074)

中值定理是可微函数的重要性质，是证明某些等式和不等式的重要工具，而等式形式的向量函数的微分中值定理一般是不成立的，通常只能得到微分中值不等式.本文从一元函数的Newton-Leibniz公式出发，证明了一个多元向量函数等式形式的积分型中值定理.该定理揭示了多元向量函数等式形式的微分中值定理不成立的原因，也蕴含了微分中值不等式.

多元向量函数； 积分型中值定理； 微分中值不等式

1　问题的提出

通用的数学分析教材在涉及多元向量函数时，只给出了微分中值不等式，例如文献[1]下册P 333定理23.14和文献[2]下册P 104定理16.2.3.特别地，文献[2]下册P 105说明了对于取值维数n≥2的向量函数只能得到微分中值不等式，而不能如数量函数那样得到等式形式的微分中值定理，并且给出下面的反例.

例1考虑定义在R2上的二维向量函数

Φ(x,y)=(excosy,exsiny)T,∀(x,y)T∈R2,

其中T表示转置.显然，Φ在整个R2上可微，且

记两点P=(0,0)T和Q=(0,2π)T，易见

Φ(Q)-Φ(P)=(0,0)T，

Φ(Q)-Φ(P)=DΦ(M)(Q-P).

关于多元向量函数的中值定理除教材[1]中形式(即本文后面的定理6和推论7)外，文献[3]得到相应的Rolle中值定理，文献[4]-[5]研究了一元向量函数的中值定理.文献[4]，对区间[a,b]上的可微函数r:[a,b]→Rn，得到一定条件下存在ξ∈(a,b)使得r′(ξ)//r(b)-r(a)的结论, 此时n=2. 文献[5]得到：存在ξ∈(a,b)使得

r′(ξ)=λ[r(b)-r(a)]，n=2，

其中λ=|r′(ξ)|/|r(b)-r(a)|；

λ1r(a)+λ2r(b)+λ3r′(ξ)=0，n=3，

其中λ1,λ2,λ3为不全为零的常数.

对n>3，得到n=3时的类似形式(高阶导数型).本论文研究思路与现有文献都不相同.

本文将从一元函数的Newton-Leibniz公式出发，证明一个多元向量函数等式形式的积分型中值定理.我们也将用此定理解释多元向量函数等式形式的微分中值定理不成立的原因，作为推论得到了微分中值不等式.

2　一元函数的Newton-Leibniz公式和中值定理

首先叙述下面一元函数的Lagrange微分中值定理(参见文献[1]上册P 123定理6.2).

定理1设函数F(t)在闭区间[a,x]上连续，在(a,x)上可导，则存在一点ξ∈(a,x)，使

F(x)-F(a)=F′(ξ)(x-a).

在定理1中，若进一步要求导函数局部可积，则有下面形式的Newton-Leibniz公式，其证明用了Lagrange微分中值定理，参见文献[1]上册P206定理9.1和P207注2.

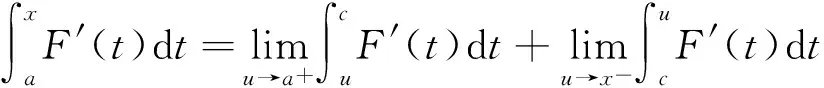
则有等式

证由假设，对每个c∈(a,x)和所有的u∈(a,c]，F′(t)在[u,c]可积.由文献[1]上册P206定理9.1和P 207注2，有

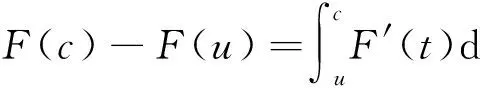
注意到F(t)在a右连续，因此

同理

对上面两个等式相加立得定理的结论.

令t=a+θ(x-a),则dt=(x-a)dθ.因此，在定理2的条件下有

(1)

公式(1)可看成积分型的中值定理，但不同于文献[8-11]的积分中值定理.我们可以用Darboux定理(参见文献[1]上册P127定理6.5)证明下面条件稍弱的积分第一中值定理，参见文献[1]上册P220定理9.7或者文献[9]P290性质6.与文献[1]上册P220定理9.7相比，我们并不要求F′(t)在闭区间[a,x]上连续.

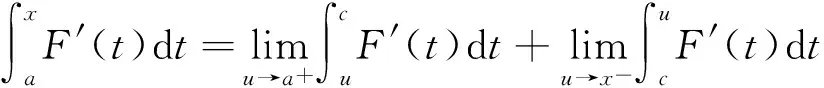
则存在一点ξ∈(a,x)，使

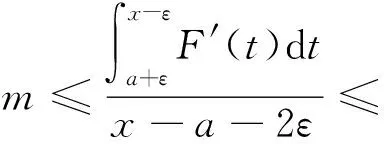
因此

由Darboux定理(参见文献[1]上册P 127定理6.5)知，存在一点ξ∈(a,x)使

注1设函数F(t)在闭区间[a,x]上连续，在(a,x)上可导.再假设a为F′(t)的瑕点，即F′(t)在a的任一右邻域上无界，但对任意的ε>0，F′(t)在[a-ε,x]有界、可积.定理2表明瑕积分

收敛，且Newton-Leibniz公式

成立.

例2设

则

由注1，有

注2条件“设函数F(t)在闭区间[a,x]上连续，在(a,x)上可导”并不蕴含导函数F′(t)在(a,x)的所有闭子集上可积.因为Riemann可积要求函数是Lebesgue测度下几乎处处连续的(参见文献[10] P57 Theorem1.7.1和 P59 Problems 3，或者文献[9]P311 的定理)，但存在满足上述条件却在正Lebesgue测度集上间断的例子(参见[11]P115例35)，因此不是Riemann可积的.

注3积分型中值定理增加了导函数F′(t)可积性的要求，因此积分型中值定理的条件比微分中值定理条件更强.但是，如果将定理中的Riemann积分换为Lebesgue积分，则积分型中值定理中对函数F(t)的要求可以减弱为F(t)绝对连续函数，其不要求F(t)在(a,x)上每点都有导数，参见文献[11]P178定理6.9.

3　多元函数的中值定理

对于多元函数情形，我们可以通过构造一个一元实值函数，利用一元函数的中值定理来得到多元函数的中值定理，具体如下.

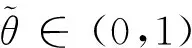
若进一步，DF(y+τ(x-y))(x-y)在(0,1)的所有闭子集上可积，则

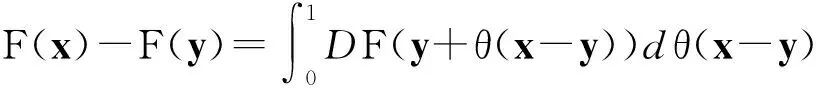
证考察辅助函数

φ(τ)=F(y+τ(x-y)),

则φ(τ)在[0,1]上连续，在(0,1)可微，且

φ′(τ)=DF(y+τ(x-y))(x-y).

若DF(y+τ(x-y))(x-y)在(0，1)的所有闭子集上可积，由定理2有

也成立.

例2设F(x,y)=xey, 则DF(x,y)=(ey,xey)，且

F(x2,y2)-F(x1,y1)=x2ey2-x1ey1.

另一方面

于是

=x1(ey2-ey1)+(x2-x1)ey2

=x2ey2-x1ey1.

故

4　多元向量函数的积分型中值定理

对于多元向量函数情形，我们自然可以对每个分量得到相应的中值定理.但是，对于所有分量却只能得到积分型中值定理，一般不能得到等式的微分中值定理，具体结论如下.

定理5设S是Rm中的凸区域， Φ是定义在S上的可微m元n维向量函数.对任意两点x,y∈S，若DΦ(y+θ(x-y))关于θ在(0，1)的所有闭子集上可积，则

(2)

其中Φ=(φ1,φ2,…,φn)T，且

证对于Φ的第i个分量φi，1≤i≤n，应用定理4的结论得

例1′再看例1，注意到

因此下面积分型中值定理成立

但是，仍有等式微分中值定理的以下变种，参见文献[1]下册 P345总练习题4，或者文献[10] P56 Lemma 2.5.1.

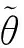
证考察辅助函数

h(τ)=αTΦ(y+τ(x-y)),

则h(τ)在[0,1]上连续，在(0,1)可微，且

h′(τ)=αTDΦ(y+τ(x-y))(x-y).

成立.

在定理6中取α=Φ(x)-Φ(y)，由Cauchy不等式以及矩阵范数与向量范数的相容性立得下面的微分中值不等式, 参见文献[1]下册P333定理23.14，或者文献[2]下册P104定理16.2.3，以及文献[10] P57 Theorem 2.5.3.

注5若在推论7中增加要求DΦ(y+τ(x-y))关于τ在(0,1)的所有闭子集上可积，则由定理5及矩阵范数与向量范数的相容性可得推论7的结论.

[1]华东师范大学数学系. 数学分析(上、下册) [M].4版.北京：高等教育出版社， 2010.

[2]崔尚斌.数学分析教程(上、中、下册) [M]. 北京：科学出版社，2013.

[3]黄土森.高维空间中的微分中值定理[J]. 宁波大学学报, 2003, 16(3): 320-322.

[4]张来亮，鞠圣会.矢性函数的拉格朗日微分中值研究[J]. 高等数学研究, 2015, 18(2): 18-20.

[5]王卫东.关于一元向量函数的微分中值定理[J]. 工科数学, 1996, 12(4): 172-175.

[6]高国成，郑艳琳，张来亮.关于积分中值定理的一个注记[J].大学数学, 2003, 19(2)：94-95.

[7]潘杰，黄有度.积分中值定理的推广及其应用[J].大学数学, 2007, 23(4)：144-147.

[8]陈玉.积分型中值定理的推广及统一表示[J].大学数学, 2015, 31(2)：61-65.

[9]卓里奇.数学分析[M].4版. 蒋铎，王昆杨，周美珂，邝荣雨译.北京：高等教育出版社， 2006.

[10]Duistermaat J, Kolk J.Multidimensional real analysis I: Differentiation[M].北京：世界图书出版公司北京公司，英文版，2009.

[11]郑维行，王声望.实变函数与泛函分析概要(第一册) [M].2版.北京：高等教育出版社， 1989.

Mean Value Theorem of Multivariate Vector Valued Functions and its Applications

HUANG Yong-zhong，LIU Ji-cheng

(School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan 430074, China)

The mean value theorem is an important property of differentiable functions, which is an important tool to prove some equalities and inequalities. In this paper, we prove a mean value theorem of the multivariate vector valued function based on the Newton-Leibniz formula. At the same time, this theorem reveals the reason of the failure for the differential mean value theorem of multivariate vector valued functions, and also implies the differential mean value inequality.

multivariate vector valued function; mean value theorem of integral type; differential mean value inequality

2015-11-05；[修改日期] 2016-04-10

湖北省教学研究项目(2013052)；华中科技大学教学研究项目(2015067)

黄永忠(1965-),男，博士，副教授，从事数学分析课程教学研究.Email:huangyz@hust.edu.cn

刘继成(1976-),男，博士，教授，从事数学分析课程教学研究.Email: jcliu@hust.edu.cn

O172.2

C

1672-1454(2016)04-0097-06