赵洪森,　曹　炜

(宁波大学数学系，浙江宁波315211)



循环矩阵与单位根

赵洪森,曹炜

(宁波大学数学系，浙江宁波315211)

研究了任意域上多项式f(x)在 m(≥degf(x))次单位根群中的零点个数与由f(x)的系数所构成的循环矩阵的秩之间的关系，推广了König-Rados定理，得到了f(x)与xm-1互素的充要条件，并给出了分解f(x)及判定f(x)是否为分圆多项式的方法.

循环矩阵； 单位根； 分圆多项式

1　引　　言

在本文中，对于给定的方阵A，用r(A)表示方阵A的秩. 用Fq表示含有q个元的有限域；对于一般的域K，用char(K )表示其特征，当K存在n次本原单位根(记为ξn)时，用Un(K)表示K中的n次单位根群，即

定义1.2称矩阵A为右循环矩阵，并记A=CR(a0,a1,…,an-1)，若

定义1.2中的右循环矩阵在文献中也被称为循环矩阵.熟知，右循环矩阵具有以下的性质.

定理1.3[1，2]对于任给的矩阵A=CR(a0,a1,…,an-1)∈n×n，设

f(x)=a0+a1x+…+an-1xn-1，

ξn为中的n次本原单位根(可取ξn=e2πi/n). 则矩阵A可对角化，且其特征值为

本文将用到另一种循环矩阵，它是一种特殊的Hankel矩阵，其定义如下:

定义1.4称矩阵A为左循环矩阵，并记A=CL(a0,a1,…,an-1)，若

定义1.5设char(K)=p,n是一个不能被p整除的正整数,ξn是上的一个n次本原单位根.则上的n次分圆多项式定义为

定理1.6[3]如定义1.5所设，并用F表示K的素域，则有

(i) deg(Qn(x))=φ(n)；

(ii)xn-1=∏d|nQd(x)；

(iii)Qn(x)∈F[x]；特别地，当K=时，Qn(x)∈[x].

定理1.7[4](König-Rados)设

f(x)=a0+a1x+…+aq-2xq-2∈Fq[x],

及A=CL(a0,a1,…,aq-2),则方程f(x)=0在Fq上非零解的个数为q-1-r(A).

2　主要结论

定理 2.1设多项式

f(x)=a0+a1x+…+an-1xn-1∈[x]，a0an-1≠0.

对于给定的正整数m≥n，设A=CL(a0,a1,…,am-1),其中ai=0,i=n,…,m-1,则当K中存在m次本原单位根时，方程f(x)=0在Um(K)中解的个数为m-r(A).

证设Um(K)中m个不同的元素分别为b1,b2,…,bm. 构造范德蒙矩阵

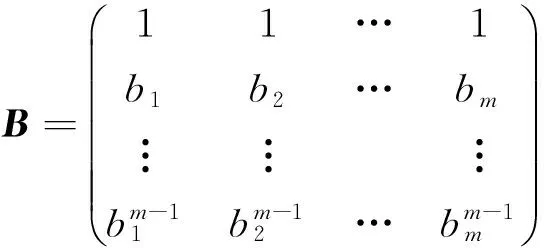
设f(x)=0在Um(K)中解的个数为N. 不妨设b1,b2,…,bm中的后N个为解, 即

由于矩阵B和

都是可逆的范德蒙矩阵，必有

即f(x)=0在Um(K)中解的个数N=m-r(A). 定理得证.

例1设

f(x)=x5+10x4+x3+10x2+11x+6∈F13[x],

解设A=CL(6,11,10,1,10,1).计算可得r(A)=3. 由定理2.1知,f(x)=0在U6(F13)中解的个数为6-3=3.

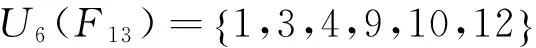
(x2-1)(x-3)|f(x),

故可得

f(x)=(x2-1)(x-3)(x2+2).

由二次互反律易知x2+2在F13中不可约. 故f(x)在F13中的因式分解为

f(x)=(x-1)(x+1)(x-3)(x2+2).

推论2.2设多项式

f(x)=a0+a1x+…+an-1xn-1∈[x]，a0an-1≠0.

对于给定的正整数m≥n，设A=CL(a0,a1,…,am-1),其中ai=0,i=n,…,m-1,则当K中存在m次本原单位根时，g(x)=xm-1与f(x)互素的充分必要条件为r(A)=m.

证g(x)与f(x)互素⟺g(x)=0与f(x)=0在域中无公共解

⟺f(x)在Um(K)中无解⟺m-r(A)=0(由定理2.1) ⟺r(A)=m.

例2在复数域上判断f(x)=2x7-x6+2x5-3x4+x3+6x-7与g(x)=x8-1是否互素?

解设A=CL(-7,6,0,1,-3,2,-1,2),计算可得r(A)=7≠m=8. 由推论2.2知，f(x)与g(x)不互素, 并且有m-r(A)=8-7=1个公共解.

例3在F11上判断f(x)=3x4+4x3+3x2+2x+1与g(x)=x5-1是否互素?

解设A=CL(1,2,3,4,3), 计算可得r(A)=5=m,故得f(x)与g(x)互素.

推论2.3设f(x)=xn+…+a1x+a0∈[x]，m≥n+1为正整数. 若p∈P(m)，令

A=CL(a0,a1,…,am-1),Ap=CL(a0,a1,…,am+m/p-1)，

其中an=1,ai=0,i=n+1,…,m+m/p-1. 则f(x)是m次分圆多项式充分必要条件为φ(m)=n且

r(A)=m-φ(m),r(Ap)=m+m/p,∀p∈P(m).

证f(x)是m次分圆多项式⟺f(x)的根恰为φ(m)个不同的m次本原单位根且它们均为单根⟺f(x)有φ(m)个单根，且若f(ξ)=0则ξm=1但ξm/p≠1对任意的p∈P(m)(由引理1.1)⟺f(x)=0有φ(m)个不同的单根且均在Um()中而在Um+m/p()中无解对于∀p∈P(m)⟺φ(m)=n且r(A)=m-φ(m),r(Ap)=m+m/p,∀p∈P(m)(由定理2.1).

例4证明在复数域上f(x)=x4+1是8次分圆多项式.

证显然,m=8,知P(m)={2}，φ(8)=4=degf(x), 令

A=CL(1,0,0,0,1,0,0,0),A2=(1,0,0,0,1,0,0,0,0,0,0,0).

计算可得r(A)=4=m-φ(m), r(A2)=12=m+m/2. 由推论2.3,f(x)=x4+1为8次分圆多项式.

[1]陈晓兰. 关于反循环矩阵的对角化问题[J]. 工科数学, 1998，16(4):130-132.

[2]吴世玗. r-循环矩阵与矩阵的对角化[J]. 工科数学, 2002，18(4):80-82.

[3]林东岱. 代数学基础与有限域[M]. 北京:高等教育出版社, 2006.

[4]Lidl R, Niederreiter H. Finite Fields[M]. Cambridge, UK: Cambridge Univ. Press, 1997:187-239.

Circulant Matrices and Roots of Unity

ZHAO Hong-sen,CAO Wei

(Department of Mathematics, Ningbo University，Ningbo Zhejiang, 315211，China)

We show that the number of zeros of the polynomial f(x) in the group of m-th roots of unity can be expressed in terms of the rank of the associated left circulant matrix, which generalizes the König-Rado theorem. As an application, the sufficient and necessary condition for f(x) to be coprime with xm-1 is obtained. We also provide the alternative approaches to factorizing f(x) as well as to determining whether f(x) is a cyclotomic polynomial.

circulant matrix; roots of unity; cyclotomic polynomial

2016-01-18；[修改日期]2016-04-16

国家自然科学基金资助项目(11371208)；宁波市自然科学基金资助项目(2016A610079)

赵洪森(1990-)，男，硕士研究生，从事数论及其应用研究.Email:1076022157@qq.com

O156

A

1672-1454(2016)04-0040-04