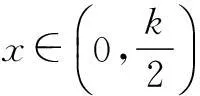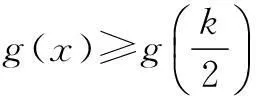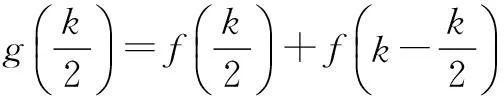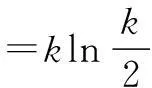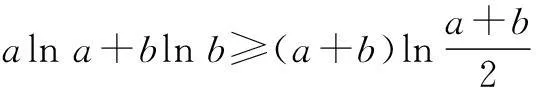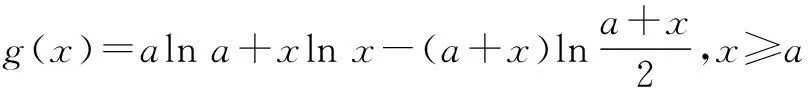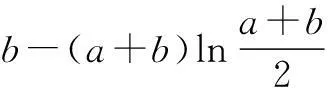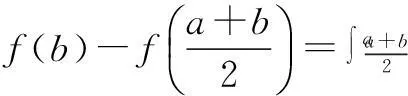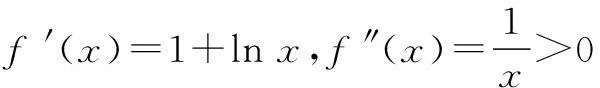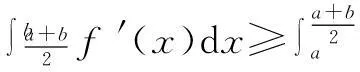对一道考题解法的多角度探讨

聂文喜

(湖北省广水市第一高级中学，432700)

一、题目与参考答案

题目(武汉市2015届高中月考题)设函数f(x)=xlnx.

(1)求函数f(x)的单调区间和最小值;

(3)若a>0,b>0,证明:f(a)+(a+b)ln 2≥f(a+b)-f(b).

本题第(1)问较为简单,第(2)问可借用第(1)问结论证明,第(3)问是二元不等式的证明,证法较多.下面对第(3)问的解法作一些探讨.

解法1(命题者提供的参考解法)

令g(x)=f(x)+f(k-x)(k>0)，

则g(x)=xlnx+(k-x)ln(k-x),

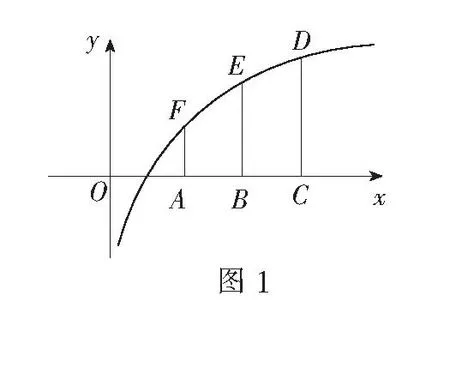
0

g′(x)=lnx+1-ln(k-x)-1

所以g(x)≥f(k)-kln 2,

即f(x)+f(k-x)≥f(k)-kln 2.

令x=a,k-x=b,则k=a+b,所以f(a)+f(b)≥f(a+b)-(a+b)ln 2,

所以f(a)+(a+b)ln 2≥f(a+b)-f(b).

评注参考答案给出的证法技巧性太强,构造函数g(x)=f(x)+f(k-x)及赋值x=a,k-x=b太巧妙,学生不易想到.下面给出第(3)问的几种易想好做的通性、通法.

二、另证

分析f(a)+(a+b)ln 2≥f(a+b)-f(b)等价于不等式

(*)

下面对不等式(*)的证法作一些探究.

解法2(主元法)不妨设b≥a.

评注(1)主元法就是将多个变量的不等式中的某个量看作主要变量(主元),将其他的变量看作参数,从而构造以主元为变量的函数,进而利用导数进行证明.

(2)题目中出现多元,若不能消元,则往往分不清主次,问题的处理就显得扑朔迷离、不得要领,所以此时最佳的做法是要有主心骨,即选定主元,则得到的就是以主元为变量的函数.

(3)主元法虽然也是利用函数思想突破关键,但是每步的操作都是十分自然与流畅,无需我们多费周折,能为大多学生所把握.因此,教师应引导学生思维,应更加注意学生对“通性、通法”的熟练掌握,而对“特殊技巧”只能在那些数学技能远高于一般同学的学生中加以倡导.

解法3(换元法)

⟺a[ln(a+b)-lna]+b[ln(a+b)

-lnb]-(a+b)ln 2≤0

构造函数g(t)=ln(1+t)

所以g(t)在[1,+∞)上单调递减,所以t≥1时,g(t)≤g(1)=0.

故原不等式成立.

解法4(放缩法)

不妨设b≥a>0,则

由不等式ln(1+x)≤x(x>-1)，得

=0，

故原不等式成立.

评注不等式ln(1+x)≤x是由课本习题ex≥x+1变式而得,ln(1+x)≤x与ex≥x+1是导数应用中的两个重要不等式,功能强大,应要求学生熟练掌握.

令F(x)=f(x)-f′(x0)(x-x0)-f(x0),则

F′(x)=f′(x)-f′(x0),

所以F′(x)在(0,+∞)上是增函数.又F′(x0)=0,∴x>x0时,F′(x)>0,0

f(x)-f′(x0)(x-x0)-f(x0)≥0.

①

②

评注切线法的实质是利用曲线的凹凸性处理不等式问题，具有高等数学背景.

解法6(积分法)不等式(*)等价于

不妨设b≥a,如图1,A(a,0),

曲边梯形BCDE的面积；

所以曲边梯形BCDE的面积大于曲边梯形ABEF的面积,所以

从而原不等式成立.