例谈高考多元最值问题的常用破解方法

胡凤琼刘少平李艾清

(湖北省仙桃市第八中学，433000)

近年来,多元最值问题深受命题者青睐．本文借助对近年来相关试题的分析,捕捉此类问题解法中的规律性因素,以期对大家有所帮助．

一、代入消元法

通过等式代入消元,减少变量的个数,化多元函数为一元函数,转化为我们熟悉的一元函数的最值问题求解．

解∵z=x2-3xy+4y2，

x,y,z为正实数，

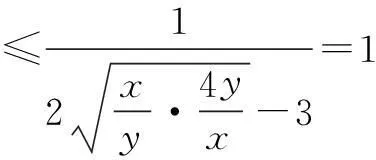
当且仅当x=2y时,取“=”.

相应的z=x2-3xy+4y2=2y2.

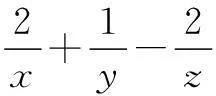
二、基本不等式法

例2(2010年重庆高考题)若a,b,c>0,且a2+2ab+2ac+4bc=12,则a+b+c的最小值是______.

解∵12=a2+2ab+2ac+4bc

=(a+2b)(a+2c)

=(a+b+c)2，

且a+2b=a+2c即b=c时等号成立.

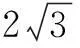
三、三角换元法

当变量之间的关系较为隐蔽不易发现时,可把问题的条件或结论作形式上的转化,借助三角换元来揭示变量之间的内在联系,把问题化难为易,化繁为简．

解由已知，可得

|2a+b|

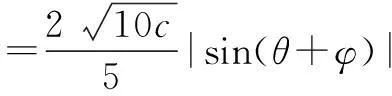
≥-2.

故所求最小值为-2.

四、柯西不等式法

柯西不等式本身具有二元或多元的形式结构,为我们解决多元变量问题提供了思路和方法．

∴(2-2z)2=(3+1)(x2+y2)

又x,y,z∈(0,1)，

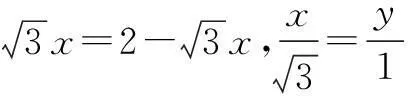
五、判别式法

某些多元变量问题,若从一元二次方程的角度来审视,使用判别式可使问题巧妙获解．

例5(2014年浙江高考试题)若实数a,b,c满足a+b+c=0,a2+b2+c2=1,则a的最大值为______.

解由a+b+c=0，得c=-(a+b)，代入a2+b2+c2=1,整理得

考虑到求a的最大值,我们可以把上式看成关于b的一元二次方程

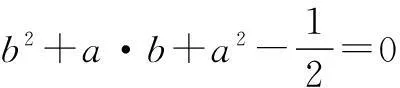
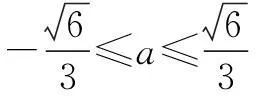
六、逐元突破法

在处理含有多变量问题时,可采取各个击破的战术,先将其中一个视为变量,其余看作参数，从而突出主要矛盾,突破参数的相互制约,化多元问题为一元问题．

解先将c看成变量,b,a看成参数,

再把b看成变量,a视为参数,令

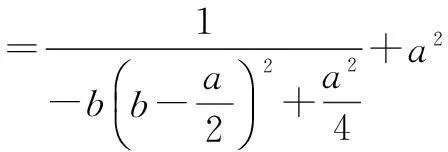
七、整体换元

把多个变量的代数式用一个新变量来替换,达到消元(减少变量)的目的,从而获得熟悉的数学模型．

解由题设，可得

八、和差代换

例8已知x,y,z∈R,且x+y+z=1,x2+y2+z2=3,则xyz的最大值是______．

解由已知条件,消去变量z，可得

x2+xy+y2-x-y-1=0.

①

令x=a+b,y=a-b，代入① 式并整理，得

b2=-3a2+2a+1≥0，

xyz=xy(1-x-y)

=(a2-b2)(1-2a)

=-8a3+8a2-1.

令f(a)=-8a3+8a2-1,则

f′(a)=-24a2+16a,

易知(f(a))min=f(0)=-1,

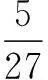
九、利用几何意义求解

某些多元函数最值问题,若单纯从代数角度去审视分析,往往不易寻找解题思路；这时,若根据函数式结构特征,联想与之相应的几何背景和模型,就可让问题迎刃而解．

例9若实数a,b,c,d满足

(b+a2-3lna)2+(c-d+2)2=0,

则(a-c)2+(b-d)2的最小值为______．

∴(a-c)2+(b-d)2的最小值为8．

十、构造函数法

多元变量问题,也可根据题设或结论所具有的特征,通过变换和构造恰当的函数,借助函数性质来解决．

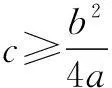
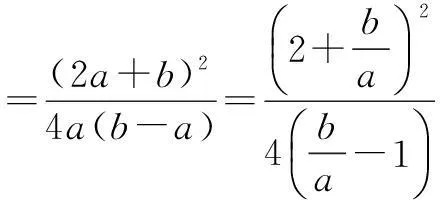
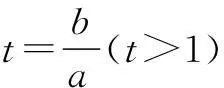
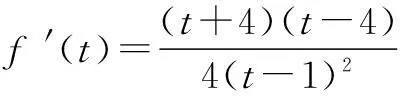
当1

当t>4时,有f′(t)>0.

故f(t)min=f(4)=-3， 于是M≥3.

故当b=4a=c时，Mmin=3.

以上给出了多元变量函数最值问题的常用方法和技巧,但这些方法和技巧并不是孤立的,而是互相联系和渗透,许多多变元问题解决往往需要综合运用多种方法和技巧,因此要认真领会每种方法实质,灵活应用．

○高考之窗○