程新跃，沈玉玲，马小玉

(重庆理工大学 数学与统计学院，重庆　400054)



引用格式：程新跃，沈玉玲，马小玉.从Berwald空间到Riemann空间的射影变换[J].重庆理工大学学报(自然科学版)，2016(1):107-110.

Citation format：CHEN Xin-yue, SHEN Yu-ling, MA Xiao-yu.Projective Changes from Berwald Spaces to Riemann Spaces[J].Journal of Chongqing University of Technology(Natural Science)，2016(1):107-110.

从Berwald空间到Riemann空间的射影变换

程新跃，沈玉玲，马小玉

(重庆理工大学 数学与统计学院，重庆400054)

摘要：给定一个n维紧致无边的微分流形M，已证明：如果≤sspan，那么从Berwald空间)到Riemann空间(M,F)的任何逐点C-射影变换均是平凡的，并且关于F是平行的。这里，表示的Ricci曲率张量关于F的迹，sspan:=trspanRic是F的数量曲率。特别地：如果，那么从Riemann空间到另一个Riemann空间(M,F)的任何射影变换都是平凡的。

关键词：芬斯勒度量；Berwald空间；射影变换；Ricci曲率；数量曲率

1预备知识

这一部分将给出芬斯勒几何中的一些定义。相关术语和记号可查阅文献[1-3]。给定芬斯勒流形(M,F)。F诱导一个射流G,其定义为

其中

Gi定义为

Gi被称为F的测地系数。芬斯勒度量F的测地线σ=σ(t)由以下方程描述：

黎曼几何中的黎曼曲率概念可以推广到芬斯勒几何中。对于任一个向量y∈TxM{0}，黎曼曲率Ry:TxM→TxM可定义为

(1)

其中

(2)

Ry是满足Ry(y)=0的线性变换，我们称R为黎曼曲率，令

(3)

(4)

易见

(5)

(6)

在式(3)和式(4)的基础上，通过直接计算可得

(7)

(8)

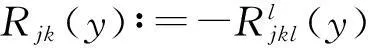
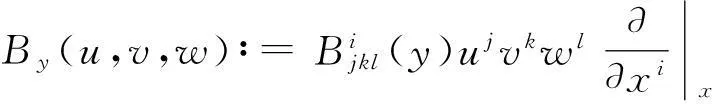
2Finsler度量的射影变换

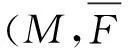
(9)

式中P称为射影因子。若P=0，称这个射影变换是平凡的，见文献[2，4-5]。

由式(9)可以得到

(10)

(11)

(12)

这里用到了以下约定：

(13)

其中P;j表示P在(M,F)上的协变导数，即

(14)

将式(12)关于yh求导，再利用式(4)可得

(15)

(16)

定义1如果Qij=0，那么芬斯勒度量的射影变换称为C-射影变换。

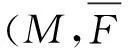
此时射影因子P就是F，则有Pi=yi/F，其中yi=gij(x,y)yj。由于F;i=0,则可以得到

为下一步研究需要提供以下引理：

引理1一个Berwald空间在射影变换下的像仍为Berwald空间，当且仅当射影因子P满足下面方程[6-7]：

(17)

很明显，如果射影变换满足式(17)，那么射影因子P可以写为以下形式

(18)

其中Ai(x)与y无关。

3主要定理

(19)

进一步假设射影变换是C-射影变换。由定义1和式(13)、(19)可知∂Aj/∂xk-∂Ak/∂xj=0,即协变向量场Ai(x)是一个局部梯度向量场。因此，M上存在一个光滑函数A(x)使得∂A/∂xi=Ai(x)，此时可以得到

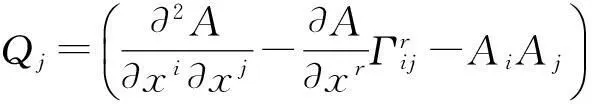
因此式(15)、(16)变为

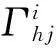
(22)

由此，可得如下定理：

证明用ghj缩并式(21)，得

即

(23)

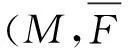
即

(24)

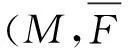
参考文献：

[1]BAO D,CHERN S S,SHEN Z.An introduction to Riemann-Finsler geometry[M].Springer Science & Business Media,2012.

[2]CHEN X,SHEN Z.A comparison theorem on the Ricci curvature in projective geometry[J].Annals of Global Analysis and Geometry,2003,23(2):141-155.

[3]SHEN Z.Differential geometry of sprays and Finsler spaces[M].[S.l.]:Kluwer Academic Publishers,2001.

[4]MATSUMOTO M.Projective changes of Finsler metrics and projectively flat Finsler spaces[J].Tensor,NS,1980,34:303-315.

[5]SHEN Z.On projectively related Einstein metrics in Riemann-Finsler geometry[J].Mathematische Annalen,2001,320(4):625-647.

[6]FUKUI M,YAMADA T.On projcctive mappings in Finsler geometry[J].Tensor,NS,1981,31:216-222.

[7]ANTONELLI P L,INGARDEN R S,MATSUMOTO M.The theory of sprays and Finsler spaces with applications in physics and biology[M].[S.l.]:Springer Science & Business Media,2013.

[8]SHEN Z.Lectures on Finsler Geometry[M].[S.l.]:World Scientific Co.,Singapore,2001.

(责任编辑陈艳)

Projective Changes from Berwald Spaces to Riemann Spaces

CHEN Xin-yue, SHEN Yu-ling, MA Xiao-yu

(College of Mathematics and Statistics,

Chongqing University of Technology, Chongqing 400054, China)

Abstract:Given a compact and boundaryless n-dimensional differentiable manifold M, we showed that any pointwise C-projective changes from a Berwald space ) to a Riemann space (M,F) is trivial if ≤sF, where denotes the trace of the Ricci curvature of with respect to F and sF:=trFRic is the scalar curvature of F. In particular, we showed that any projective change from a Riemann space ) to another Riemann space (M,F) is trivial if ≤sF.

Key words:Finsler metric; Berwald space; projective change; Ricci curvature; scalar curvature

文章编号：1674-8425(2016)01-0107-04

中图分类号：O186.1

文献标识码：A

doi:10.3969/j.issn.1674-8425(z).2016.01.019

作者简介：程新跃(1958—), 男, 重庆人, 博士，教授, 主要从事微分几何研究。

基金项目：国家自然科学基金资助项目(11371386); 欧盟FP7(SEVENTH FRAMEWORK PROGRAMME)资助项目(PIRSES-GA-2012-317721).

收稿日期：2015-09-19