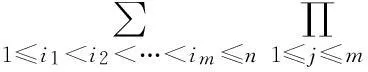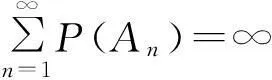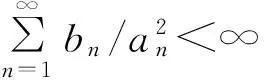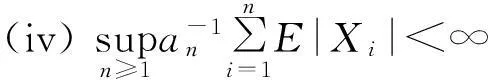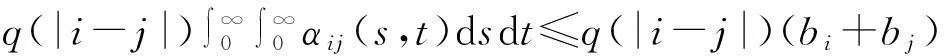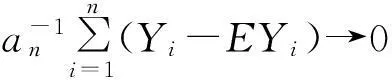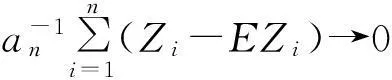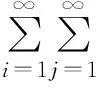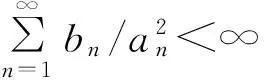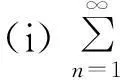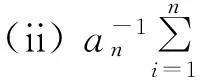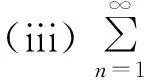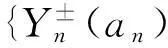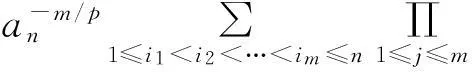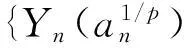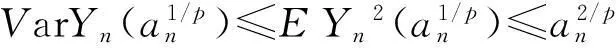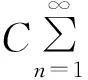程，许雪

(湖北大学数学与统计学学院,湖北 武汉 430062)



AQSI序列部分和与乘积和的强大数定律

(湖北大学数学与统计学学院,湖北 武汉 430062)

摘要：研究AQSI序列部分和与乘积和的强大数定律，得到不同分布AQSI序列部分和与乘积和强大数定律成立的充分条件.

关键词：AQSI序列;部分和;乘积和;强大数定律

0引言

定义1[1]称随机变量序列{Xn,n≥1}是渐近象限次独立(asymptotically quadrant sub-indenpendent, AQSI)的，若存在正数序列{q(m),m∈N},满足m→∞时，q(m)→0,且对任意i≠j均有

P(Xi>s,Xj>t)-P(Xi>s)P(Xj>t)≤q(|i-j|)αij(s,t),s,t>0,

P(Xi

其中αij和βij是非负函数.

AQSI序列的概念是由Chandra和Ghosal[1]首先提出的，由AQSI序列的定义可知AQSI序列是包含独立序列的一类非常广泛的随机序列.由于AQSI序列条件较弱，因此研究也较为困难，所获结果也不太多.Ghosal等[2]讨论了AQSI序列加权的Marcinkiewicz-Zygmund型强大数定律和加权和的强大数定律，唐键等[3]研究了AQSI序列的几乎处处收敛性和强大数定理.本文中研究了AQSI序列部分和与乘积和的强大数定律，得到不同分布AQSI序列 部分和与乘积和强大数定律成立的充分条件.文中C是正的常数，在不同的地方可取不同的值.对随机变量序列{Xn,n≥1}及a>0,恒记Yn(a)=-aI(Xn<-a)+XnI(|Xn|≤a)+aI(Xn>a).

1引理

为了得出本文中的主要结论，本节先给出一些相关的引理.

引理1[1]设{Xn,n≥1}是AQSI序列，如果{fn,n≥1}是非降(或非增)函数，则{fn(Xn),n≥1}仍然是AQSI序列.

引理2[4]对任意的实数列{xn,n≥1}, 及对任意的n≥m≥1,有

引理3[5](推广的Borel-cantelli引理)设{An,n≥1}是事件列:

2主要结果及证明

(i) 对任意的i≠j有

(1)

(ii) 对任意的i≠j有

(2)

于是

同理可得

Xn-EXn=Yn-Zn,

又因为

为证

只需证明

以及

由于

(3)

又因为

(4)

又由条件(iii)有

(5)

推论1的证明由条件(i)知

(6)

即可.

(i)gn(x)在(0, ∞)内单调不减,且当0

(ii)

同时当p∈[1,2)时,若有

(7)

以及

(8)

则

(9)

进一步我们有,对任意的m≥1,

(10)

在条件(i)下,gn(x)在(0, ∞)内不减,以及gn(1)≥λ.可知

(11)

其次,又因为

于是由Kronecker引理知

(12)

由于

(13)

接下来,对给定的m≥1,由引理2可知要证(11)式成立,只需证明,对任意的1≤r≤m,都有

(14)

由Cr不等式得

从而要证(14)式对r=1,2,…,m成立,只需证明(14)式对r=1,2成立即可,其中当r=1时,上述已证,当r=2时,由Borel-Cantelli引理及(11)式只要证

(15)

推论2的证明显然fn(x)=|x|r为在(0, ∞)内取正值的偶函数.

当r∈(0,1]时,在区间(0, ∞)内有下面式子成立,fn(x)在(0, ∞)内不减,x/fn(x)=|x|1-r=x1-r在(0, ∞)内不减. 因为

所以

从而满足定理2的条件(i).

当r∈(1,2]时,在区间(0, ∞)内有下面式子成立,fn(x)/x=|x|r/x=xr-1,当x增大时,xr-1不减,即fn(x)/x在(0, ∞)内不减.x2/fn(x)=x2/|x|r=x2-r,当x增大时,x2-r不减.即x2/fn(x)在(0, ∞)内不减. 因为

所以

又因为当r∈(1,2]时,EXn=0,n≥1,从而fn(x)满足定理2的条件(ii).

综上可述，推论2的结论成立.

则(9)式, (10)式成立.

推论3的证明当条件(i)成立时,取

gn(x)=|x|r/(1+|x|r), 0

当条件(ii)成立时,取

还有

还有

因此,若条件(i)被满足,则

若条件(ii)被满足,则

于是由定理2可知推论3成立.

参考文献3

[1] Chandra T K, Ghosal S. Extensions of the strong law of large numbers of Marchinkiewicz and Zygmund for dependent variables[J]. Acta Math Hung，1996,71(4)：327-336.

[2] Chandra T K, Ghosal S. The strong law of large numbers for weighted averages under dependence assumptions[J]. Theoret Probab，1996,9(3):797-809.

[3] 唐健,汪忠志.关于AQSI序列的几乎处处收敛性及强大数定理[J].数学的实践与认识,2012,42(4):172-178.

[4] 王岳宝,严继高,成凤，等.关于不同分布的两两NQD序列的Jamison型加权乘积和的强稳定性[J].数学年刊,2001,22A(6):701-706.

[5] 吴群英.混合序列的概率极限理论[M].北京:科学出版社,2005.

[6] Chandra T K. Uniform integrability in the Cesàro sence and the weak law of large numbers[J]. Sankhya:the Indian Tournal of statistics,1989,51(A):309-317.

(责任编辑赵燕)

The strong law of large numbers of partial sum and sum of products for AQSI sequence

CHENG Yan，XU Xue

(Faculty of Mathematics and Statistics, Hubei University, Wuhan 430062,China)

Abstract:We studied the strong law of large numbers of partial sum and sum of products for AQSI sequence, and then we obtained the sufficient conditions in which the strong law of large numbers of partial sum and sum of products for AQSI sequence was established.

Key words:AQSI sequence; partial sum; sum of products; strong law of large numbers

中图分类号:O211.4

文献标志码:ADOI:10.3969/j.issn.1000-2375.2016.01.002

文章编号:1000-2375(2016)01-0007-07

作者简介:程(1991-)，男，硕士生，E-mail:1772461985@qq.com

收稿日期:2015-06-24