田文凯

(西安电子科技大学数学与统计学院，陕西西安 710126)

近年来，进化算法由于强大的实际应用能力得到了快速发展。各种进化算法如雨后春笋般相继而出。在长期的实践检验中，主流的进化算法大致有(1)粒子群算法(PSO)［1］。(2)蜂群算法(ABC)［2］。(3)差分进化算法(DE)［3］。(4)协方差矩阵算法(CMAES)［4］，以及它们相应的改进算法，如基于粒子群算法改进的CLPSO［5］，PSO2011［6］，基于差分进化算法改进的JDE［7］，SaDE［8］，基于 ABC 改进的 GABC［9］等。

回溯搜索优化算法(BSA)是Civicioglu于2013年提出的一种基于种群的新进化算法，其算法框架类似于差分进化算法，但在变异操作或者扰动策略，和交叉操作或者混合策略上，与差分进化算法有本质的区别。它的扰动策略和混合策略新颖高效，在全局搜索能力和收敛速度方面表现良好，使其在与 PSO，ABC，CMAES，JDE，SADE 的比较中，显出较大的优势［10］。BSA应该会成为继以上算法后的一个新主流进化算法。

1 BSA的介绍

BSA的算法框架与差分进化算法相似，但BSA有两个选择过程，分别称为选择I和选择II。选择I为变异策略中随机选择一个历史种群，用于产生差分量，选择II用于更新种群。总体算法框架可分为初始化种群，选择I，变异，交叉，选择II 5部分。

BSA算法的逻辑框架如下:

(1)初始化种群。

1.1 初始化种群

BSA的初始化种群与差分进化算法相同，但BSA的初始化种群P包括种群old P的初始化和历史种群的初始化

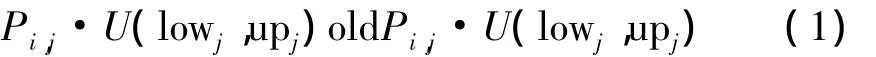
其中 i=1，2，3…，popsize;j=1，2，3…，D，popsize 是种群规模，D是问题维数，lowj，upj分别表示第j维分量的下界和上界，U 表示均匀分布，Pi，j，old Pi，j是(lowj，upj)上服从均匀分布的随机数。两初始化过程相互独立。对old P的初始化是为了防止第一次执行选择I时，old P值为空，以保证算法的可行性。

1.2 选择 I

BSA的选择I用于选择一个新的历史种群old P，其算法思想如式(2)所示

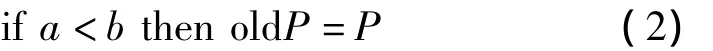
其中，a，b是(0，1)上服从均匀分布的随机数。式(2)的作用是在前代种群中选择一个历史种群，并记住这个历史种群直至再次发生改变，当代历史种群old P可以是前n代种群中的任何一代以及初始的历史种群，其中n=1，2，…，N－1，N是当前已迭代的最大代数。

1.3 变异

在old P的值确定后，对old P中的个体进行随机排序，并重新赋予old P。利用式(3)进行变异

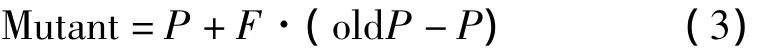
这里F是变异尺度系数用以控制变异的幅度;F=3·randn，randn是一服从标准正态分布的随机数。

1.4 交叉

BSA的交叉策略是一种基于两种交叉方式等概率调用的联合交叉策略，相比差分进化算法较为复杂。BSA在交叉时，首先选择一个交叉长度n，然后将父代种群P中每个个体随机选取n个元素与Mutant中的相同位置个体的同维元素进行互换，生成新的个体，其中n是(0，mixrate·D)中的整数。但在每代交叉时，n的选择有两种可能，根据n的赋值方式，做以下分类叙述:

(1)交叉策略I:n恒为1。

(2)交叉策略II:先给每个个体随机生成一个随机数 rand·U(0，1)，以

为交叉长度。其中mixrate是交叉概率，D是问题维数即染色体长度。

两种交叉策略等概率随机调用构成BSA的交叉策略。在式(3)中，Mutant的元素有可能超出相应分量的取值范围，若交换到此类元素，将重新在相应的取值区间内随机选择一个值，最终生成新一代试验种群T。

1.5 选择 II

比较P和T同位置个体的适应度，当T中第i个个体Ti的适应度小于Pi时，便用Ti代替Pi更新当代种群，如式(5)所示

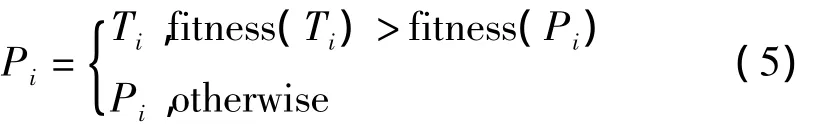
更新后的种群进入下一代循环。

2 BSA的改进

长期以来，进化算法总是在收敛速度和全局搜索性之间做改进，如何在保证算法全局收敛性的前提下，加快收敛速度，是改进进化算法的主要目标之一。本文经过实验数据分析，对BSA的变异尺度系数和交叉策略做了相应改进，使得BSA的收敛速度和收敛结果都有了一定的提高。

2.1 BSA变异尺度方程的改进

BSA的变异尺度系数F=3·randn，其容易产生过大或过小的随机值，过大的变尺度系数会降低算法的收敛性，过小的变异尺度系数会增加算法陷入局部最优解的可能性，所以本文提出了一种新的变异方程

其中randperm(old P－P)表示old P－P中行向量的一个随机重排。假设old P－P中行向量的方差为Var(old P－P)，则有 Var(randperm(old P－P))=Var(old P－P)，所以有

Var［0.5·(old P － P)+0.5·randperm(old P －P)］=0.5·Var(old P －P)

差分量方差比原来减小了一半，意味着新变异形式能有效减少过大或过小扰动量的产生。而两个随机差分量合成扰动量的方式使引导方式由线性引导变为非线性引导，所以负变尺度系数失去意义，不是必须的。

在改进变异尺度系数时，本文参考了物理学中的一些分布，令变异尺度系数是服从麦克斯韦－玻尔兹曼分布的随机数，麦克斯韦－玻尔兹曼分布描述的是处于热平衡态下理想气体分子速率的分布，能进一步减小方差，且大量数值实验表明，麦克斯韦－玻尔兹曼分布能有效地扰动种群，使变异过程出现更好的实验种群。图1说明新的变异尺度系数具有更好的搜索性能。新变异尺度系数为

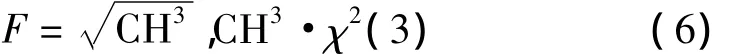
χ2(3)是自由度为3的卡方分布，CH3是服从χ2(3)随机数。图1～图5是原算法和改进变异系数的算法在测试函数F1～F5上的收敛效果比较，可以看到新的变异尺度系数在多峰函数的测试中有较好的收敛效果。

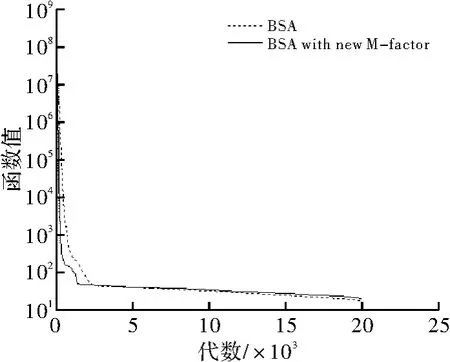
图1 测试函数F1收敛速度对比

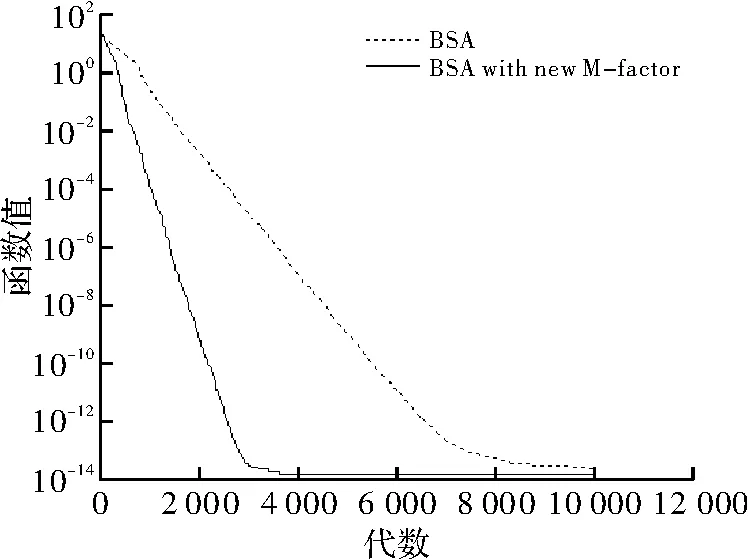
图2 测试函数F2收敛速度对比图

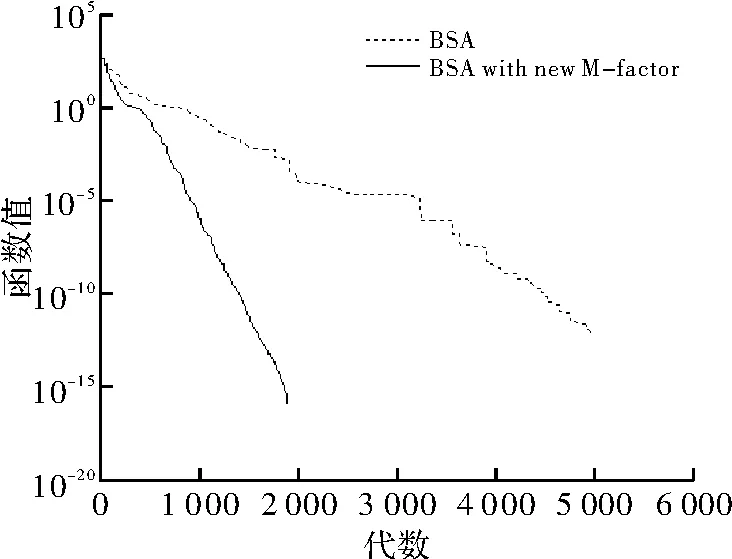
图3 测试函数F3收敛速度对比

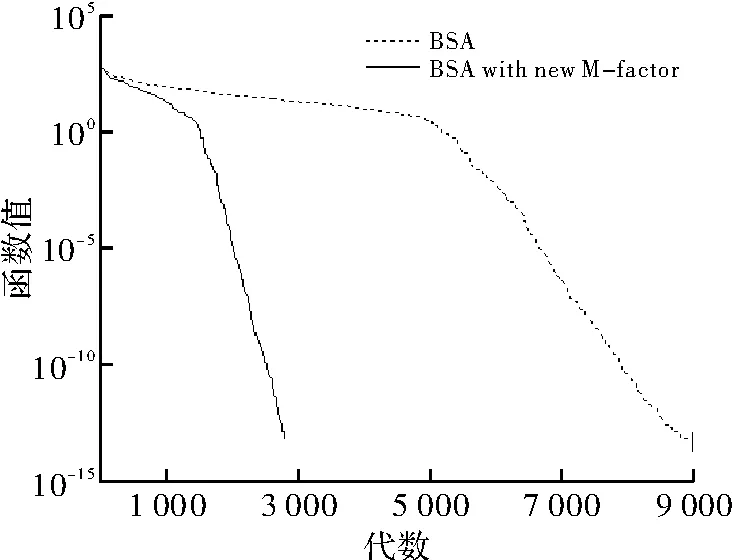
图4 测试函数F4收敛速度对比

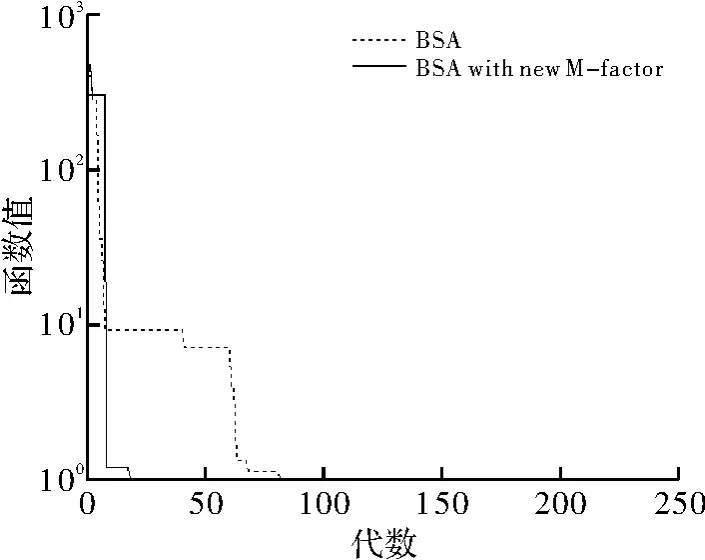
图5 测试函数F5收敛速度对比

2.2 BSA交叉策略的改进

实验表明，单独使用交叉策略I或者交叉策略II，收敛速度比联合交叉策略慢得多，联合交叉策略对BSA良好的收敛效果有较大贡献。而受到JADE［11］中交叉率产生方式的启发，在联合交叉策略的随机选取过程中加入了一定的自学习性，使收敛的效果有了进一步提高。

原联合交叉策略中，两种交叉策略的选取是随机的，即从(0，1)上均匀选取随机数a，b以a，b的大小来选择进行哪种交叉;在改进的交叉策略中，我们只生成一个随机数a，以a和自适应概率分度p的大小来决定，当a＜p时，进行交叉策略I，否者进行交叉策略II，其中 p·N(cr，0.25)，N(cr，0.25)是以 cr为中心，以0.25为方差的正态分布。以随机数a，b的大小来决定选择哪种交叉策略，使得交叉过程有些盲目，而以概率分度p和a进行比较便使得两种交叉策略的选择有一定的偏向。每进行per代进化后，将对cr进行一次更新，cr的更新策略如下:

首先，定义种群的一个进化评判度Δs，如式(7)

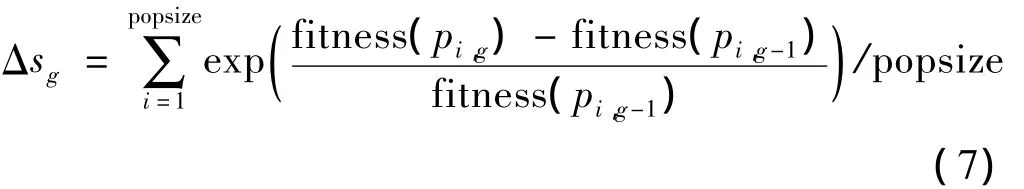
g是代数，g－1代表 g的上一代，g=1，2，…，epoch，epoch是最大进化代数，pi，g是g代种群中第i个个体，当 g － 1 为 0 时，pi，g－1表示初始种群的个体，fi，g为 pi，g的函数值，适应度值定义为

定义两种交叉策略的收敛效果评判度cr1和cr2

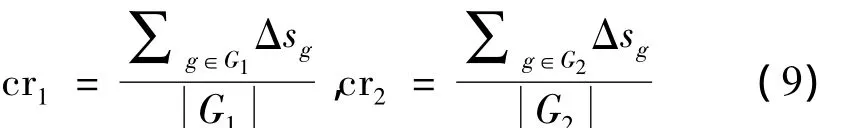
G1，G2分别代表进行交叉策略I和交叉策略II的代数集合表示G1，G2中元素的个数。如果进行per了次迭代，cr将如下进行更新

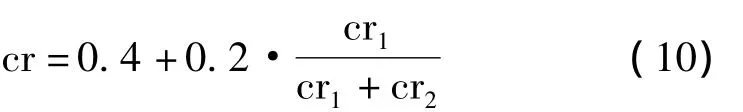
同时，cr1和 cr2重新归零，G1和 G2重新置为空集，其中cr的初始值为0.5。这样，算法将吸取上per代的经验，为下per次迭代规划一个新的cr。为说明新的交叉策略的效果，在相同的变异策略下，即不更改变异尺度系数的情况下，单独比较了新交叉策略和原交叉策略的收敛效果，结果如图6～图10所示(F1～F4中，per=200，F5中，per=20)。

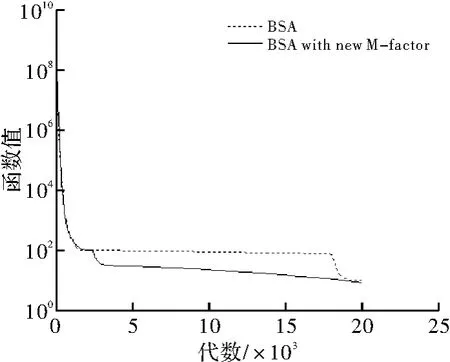
图6 测试函数F1收敛速度对比

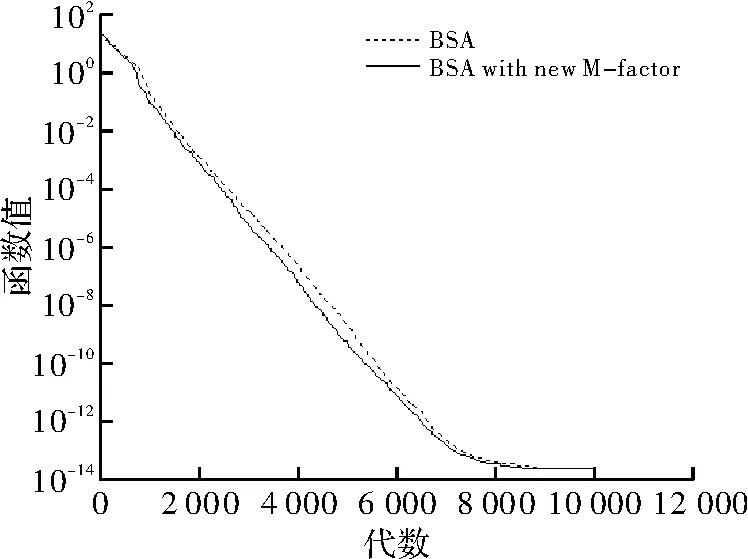
图7 测试函数F2收敛速度对比

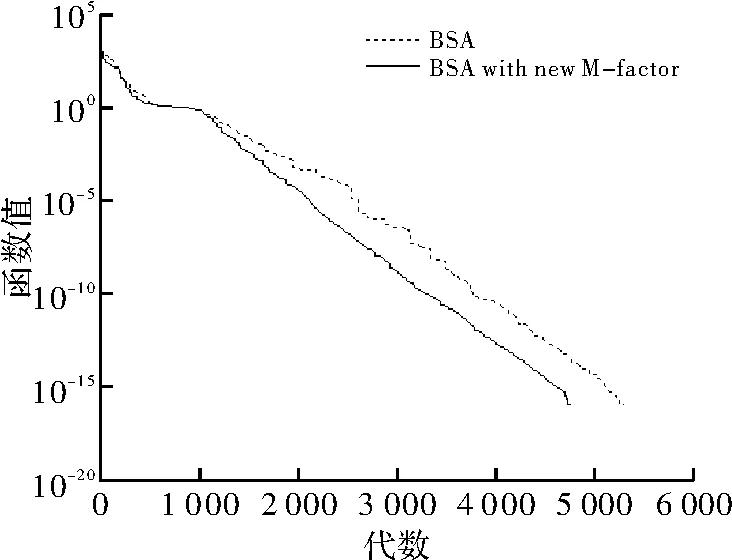
图8 测试函数F3收敛速度对比

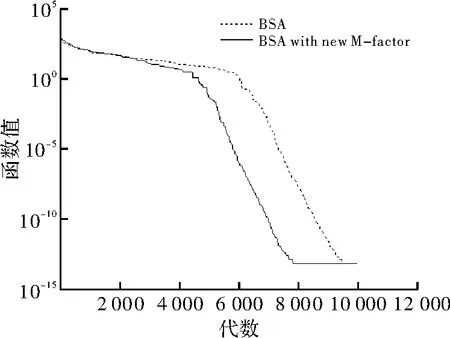
图9 测试函数F4收敛速度对比

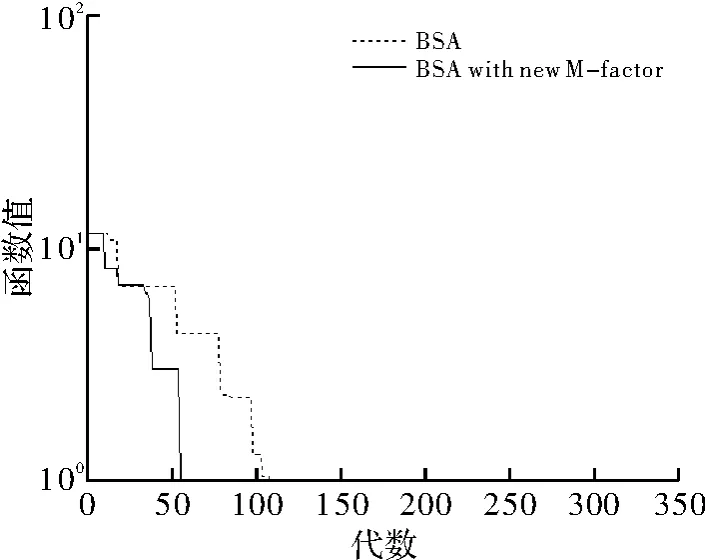
图10 测试函数F5收敛速度对比

新交叉策略在算法效果上有一定的提高，但遗憾的是，新交叉策略的改进效果并不明显，交叉策略还需要有更合理判定准则的引入和参数调整。

3 数值实验

实验分为测试函数选取，停止条件制定和测试结果的统计分析3部分。

3.1 Benchmark测试函数选取

数值实验选取了15个函数进行测试，其中有5个高维单峰函数，5个高维多峰函数和5个限定维多峰函数，如表1所示。

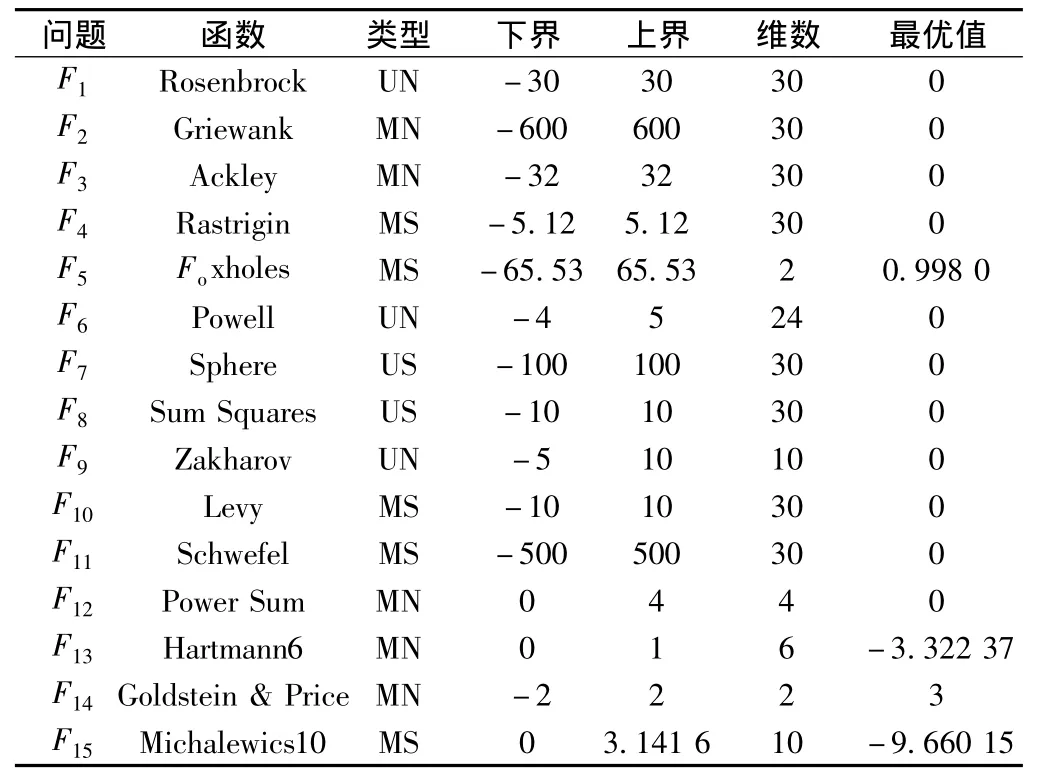
表1 测试用到的Benchmark测试函数

表1中，M为Multimodal(多峰)，N为Non－Separable(不可分)，U 为Unimodal(单峰)，S 为Separable(可分)。

3.2 停止条件制定与参数选取

(1)所求结果与Benchmark测试函数的已知最优解的绝对差＜10－323时，停止。

(2)到达最大进化代数epoch时，停止。

最大进化代数epoch根据每个测试函数的性质选定，如表3所示。实验参数取值如表2所示。

表2 测试中的实验参数取值

实验均在相同配置的计算机上，使用Matlab2013a进行编程测试。

3.3 测试结果的统计分析

进化算法的结果是随机的，每次运行结果都是一个最优解的近似值，同一进化算法对同一测试函数的运行结果也并不稳定，所以不能凭借一次运行结果来比较算法的优劣。在测试中，对于同一Benchmark函数分别运行IBSA和BSA的程序30次，比较30次运行结果的均值和方差，以评定BSA和IBSA的收敛效果。30次结果的均值与方差如表3所示。

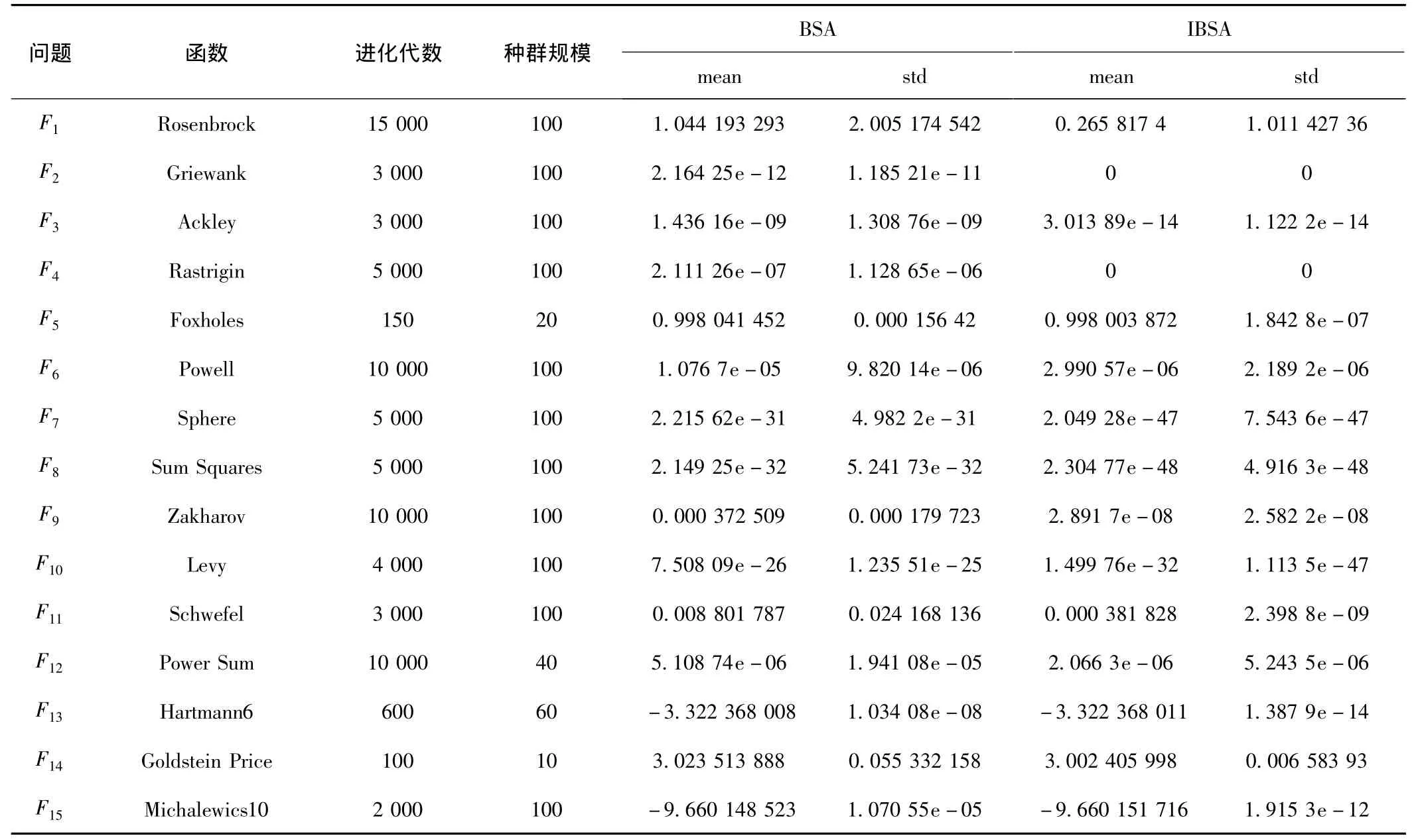
表3 由BSA和IBSA获得相应测试函数30次测试结果的均值与方差

从15个测试函数的结果可以看出，IBSA的收敛效果均优于BSA，且对高维多峰函数在较长的进化代数下，IBSA取得的结果仍然优于BSA，可见IBSA不仅具有较快的收敛速度，也表明了IBSA同时具有良好的全局搜索性能。

4 结束语

在数值实验中，IBSA取得了较大的优势，这归功于其更加有效的变异尺度系数和智能化的交叉选择策略，两者使IBSA在处理种群中比BSA更加高效和更有针对性;同时，新的变异尺度系数和交叉选择策略的智能化设计注重对原有算法的继承，从而使IBSA和BSA一样具有良好的全局搜索性能。IBSA较成功地在保证算法全局收敛性的前提下，加快了收敛速度。但IBSA的交叉策略并没有大幅提高算法的收敛性能，其控制结构和相关参数还需进一步的改进和调整。

［1］Eberhart R，Kennedy J.A new optimizer using particle swarm theory［C］.Proceedings of the Sixth International Symposium on Micro Machine and Human Science，MHS'95.，IEEE，1995.

［2］Karaboga D，Basturk B.A powerful and efficient algorithm for numerical function optimization:artificial bee colony(ABC)algorithm［J］.Journal of Global Optimization，2007，39(3):459－471.

［3］Price K V.Differential evolution:a fast and simple numerical optimizer［C］.Fuzzy Information Processing Society，1996 Biennial Conference of the North American，IEEE，2009.

［4］Dorigo M，Maniezzo V.Ant system:optimization by a colony of cooperating agents［J］.IEEE Transactions on Systems，Man，and Cybernetics－ Part，1996，26(1):29 －41.

［5］Liang J J，Qin A K，Suganthan P N，et al.Comprehensive learning particle swarm optimizer for global optimization of multimodal functions［J］.IEEETransactions on Evolutionary Computation，2006，10(3):281 －295.

［6］Thangaraj R，Pant M，Ajith Abraham，et al.Particle swarm optimization:Hybridization perspectives and experimental illustrations ［J］.Applied Mathematics and Computation，2011，218(12):5208 －5226.

［7］Qin A K，Huang V L，Suganthan P N，et al.Differential evolution algorithm with strategy adaptation for global numerical optimization［J］.IEEE Transactions on Evolutionary Computation，2009，13(2):398 －417.

［8］Brest J，Greiner S，Boskovic B，et al.Self－ adapting control parameters in differential evolution:A comparative study on numerical benchmark problems［J］.IEEE Transactions on Evolutionary Computation，2006，10(6):646 －657.

［9］Zhu G，Kwong S.Gbest－ guided artificial bee colony algorithm for numerical function optimization［J］.Applied Mathematics and Computation，2010，217(7):3166 －3173.

［10］Civicioglu P.Backtracking search optimization algorithm for numerical optimization problems［J］.Applied Mathematics and Computation，2013，220(15):8121 －8144.

［11］Zhang J，Sanderson A C.JADE:adaptive differential evolution with optional external archive［J］.IEEE Transactions on Evolutionary Computation，2009，13(5):945 －958.

［12］Molga M，Smutnicki C.Test functions for optimization needs［M］.Berlin:Test Functions for Optimization Needs，2005.

［13］Karaboga D，Akay B.A comparative study of artificial bee colony algorithm ［J］.Application Mathematical Computation，2009，216(1):108 －132.