向少华，赖青青，陈英

（怀化学院电气与信息工程学院，湖南怀化418008）

三角形在位势下一维无限深势阱中粒子的量子特性研究

向少华，赖青青，陈英

（怀化学院电气与信息工程学院，湖南怀化418008）

利用有限差分方法数值求解了具有三角形在位势的一维无限深势阱中粒子的运动学方程，讨论了在位势对粒子几个最低能量本征值和与其对应的概率密度分布函数的影响.结果表明：粒子的最低能量随在位势强度的增加而增大，而它们的概率密度分布函数则呈现各不相同的空间特性.基态概率密度分布函数的波峰朝左移动，第一激发态的波峰朝右移动，而第二激发态的两侧波峰被削弱，中心峰被增强.

量子力学；无限深势阱；三角形在位势；有限差分法

在量子力学的建立过程中，一维无限深势阱模型是最简单但又最重要的量子体系.该体系的理论成果为我们展示了量子力学在描述微观粒子行为上要比经典物理更精确、更准确和更高级.长期以来，人们围绕该模型定态薛定谔方程求解以及边界条件等问题进行了广泛而深入的研究.在势函数较为简单的量子体系中，通常是直接求解这个二阶偏微分方程，或者在能量算符表象下，将薛定谔方程转化为哈密顿算符的本征方程，求出它的本征值和本征函数，按能量本征函数展开所求波函数［1］.但对于复杂的势函数，量子体系薛定谔方程的求解十分困难，得不到解析解.一般采取数值计算方法讨论这些复杂量子体系的量子特性.在这些近似处理方法中，有限差分方法是简便而有效的方法之一.该方法已被人们运用到一维无限深势阱模型［2，3］，一维线性谐振子模型［4，5］和氢原子体系［6］等.本文将利用有限差分方法研究一类新颖的一维无限深势阱模型，即微观粒子囚禁在一个无限深势阱中且势阱底部还有一个三角形势场的作用.我们讨论的模型具有一定的理论指导意义.因为在实际金属中，电子并非是自由的，它们还受到金属中杂质、缺陷和晶格振动等的影响，使电子处在有势函数涨落的阱底运动［7］.

1 具有三角形在位势的一维无限深势阱模型的理论描述

无在位势的一维无限深势阱模型（或称为经典无限深势阱模型）中，微观粒子的运动遵循薛定谔方程

式中u是粒子的质量，E为粒子的能量本征值，Ψ（x）是与之对应的能量本征函数，U（x）为势阱函数，其形式为

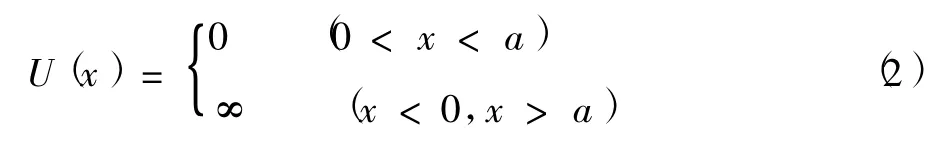
上式中a为势阱宽度.假设粒子的能量满足0＜E＜V0并根据波函数标准化条件，不难得到粒子的能量本征值为

和对应的本征函数是

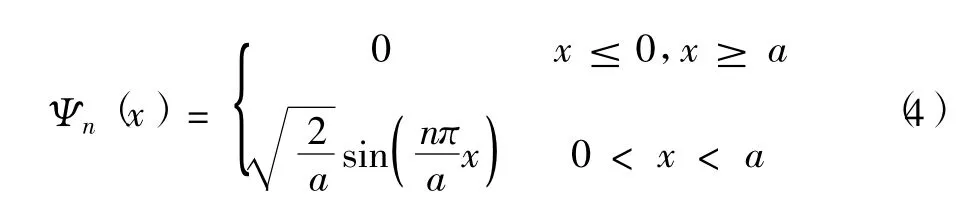
由此看出：与经典粒子不一样，在无限深势阱中，粒子的能量是分立，不是连续的；n＝1时能量最小，叫基态能量（E1≠0）或零点能，n＝2为第一激发态，n＝3为第二激发态，其它的依此类推.因此，粒子在无限深势阱中运动表现为量子化效应.

无在位势的无限深势阱模型是量子力学中仅有的几个可以精确求解的理论模型.在上面的例子中，势阱底部势函数为零，即为平坦的.在本文中我们讨论一类特别的理论模型，其阱底部势函数如图1所示，称为三角形在位势.由于它的作用，使定态薛定谔方程成为一个变系数的二阶偏微分方程，求解异常繁琐与困难，故我们采取有限差分方法研究粒子的能量本征值和本征函数，进而讨论概率密度分布函数.

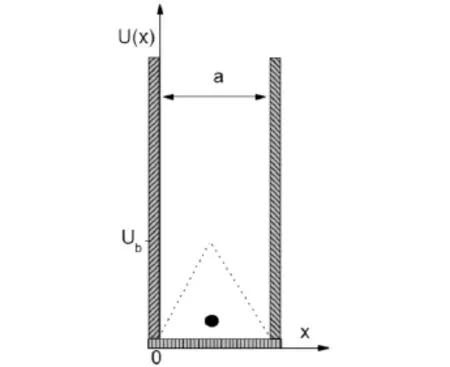
图1 具有三角形在位势的一维无限深势阱模型

在利用有限差分方法处理薛定谔方程时，我们将粒子的波函数和哈密顿能量算符作如下变换

这样偏微分方程就转化为矩阵方程，即转化为

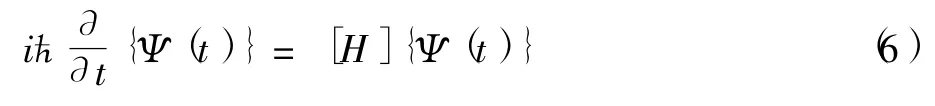
同时将势阱空间无限划分，切割成N个空间格点，格点间的晶格常数为Δx＝b，于是我们用列矢量｛Ψ（x1），Ψ（x2），…，Ψ（xN）｝T表示粒子在时间t的波函数Ψ（x，t）.

接下来求哈密顿算符

的矩阵形式.根据有限差分方法，我们将波函数对空间坐标的二阶微分用下式代替

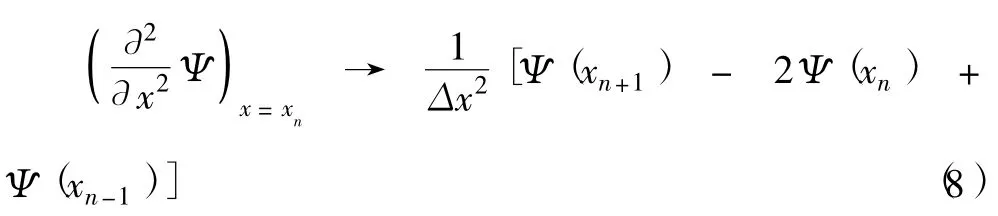
和

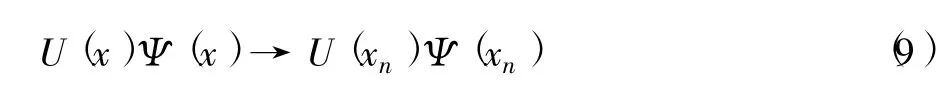
从而有：

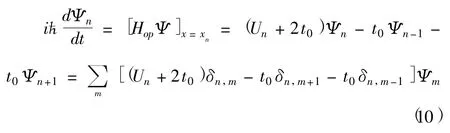
这里与格点坐标相关的物理量省略了对应的坐标，而用编号代替，如Ψ（xn）用Ψn表示，U（xn）用Un表示，等等，t0＝ħ2／2ub，δn，m为克罗内克符号.

由方程（10）可知，哈密顿量算符的矩阵元是

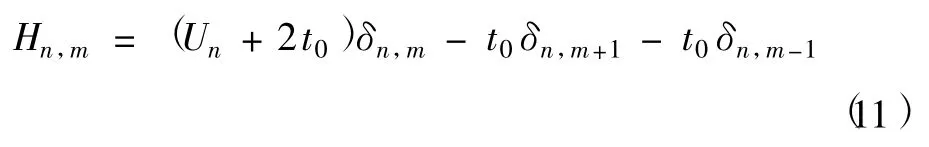
因此，一旦对势阱宽度划分确定后，我们就可以写出哈密顿矩阵，其表达式是

假设哈密顿矩阵（12）的本征值为Eα，与其相对应的本征矢为｛α｝，则哈密顿量矩阵方程的解是

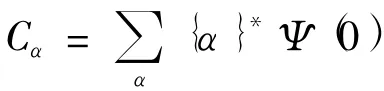
2 粒子能量本征值和概率密度分布函数分析与讨论

根据前面的理论知识，我们借助于Matlab软件数值计算粒子在具有三角形在位势的一维无限深势阱中的能量本征值和概率密度分布函数.在数值计算中我们设势阱宽度为120 nm，势阱区域划分为120个格点数，三角形在位势的数学表达式假设为

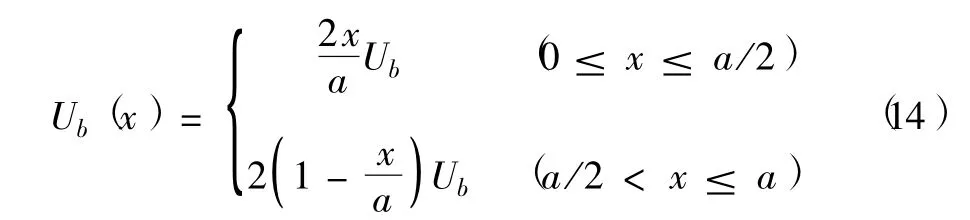
式中Ub为在位势强度，模拟中其单位为eV.

表1是在各种三角形在位势作用下粒子前四个能量本征值，其中Ub＝0为经典的无限深势阱的情况.

表1 三角形在位势作用下粒子的前四个最低能量值

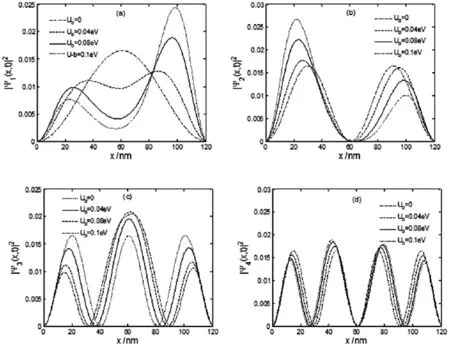
图2 不同三角形在位势下粒子前四个概率密度分布函数

从表1中可以看处，在三角形在位势的作用下，粒子的最低几个能级的能量将会增加.这种增加可以根据量子力学基本原理得到解答.众所周知，粒子的能量等于动能与势能之和，即：E＝p2／2u＋U（x），因此，在位势的作用相当于给粒子施加了一作用力，使粒子的能量发生改变.在本例子中，我们的在位势始终为正，故而能量增加，能级向上移动.同时，我们从图2中发现：在在位势的作用下，各级能量本征值的概率密度分布函数不再是正弦变化，展现出了丰富、有趣的物理信息.对于基态和第一激发态概率密度分布函数，随着在位势的增加，它们不再是对称分布的，它们的波峰将发生漂移.基态概率分布函数的波峰朝右移动，而第一激发态的波峰朝左移动，第二激发态概率密度分布函数的中心波峰振幅被增强，而两侧的波峰被削弱.这些结果也表明在在位势的作用下，粒子的宇称遭到了破坏.我们知道，在经典的无限深势阱模型中，由于势阱函数有U（x）＝U（－x），则量子系统具有确定的宇称.但粒子在三角形在位势的驱动下，势阱函数U（x）＝U（－x）不再成立，因而，该囚禁粒子系统没有明确的宇称，波函数表现为非奇非偶.此外，我们由图2可以推知，施加的在位势不改变波函数波节的个数，却改变了波函数节点（波函数为零的地方）出现的位置.正如文献［8］所述，有限差分法计算得到的结果只在最低几个能量值与解析结果相一致，而在高能态情况，它们偏离很大.这种差异主要是有限差分法只考虑到二阶项，忽略了三阶以上的项.因此，对于高阶能量本征值和本征函数情况则需采用其它的近似处理方法.

3 结论

本文采用有限差分方法和Matlab数学软件，数值计算了粒子在一维无限深势阱且阱底有一个三角形在位势的模型中几个最低能量本征值和相应的概率密度分布函数.结果表明施加的在位势对粒子本征值能量及本征函数有显著的影响.与经典无限深势阱模型相比，尽管在位势不改变粒子波函数节点个数，但使节点出现的位置坐标发生了移动，更使概率密度分布函数呈现出了空间分布的非对称性.这些有趣的现象对全面认识无限深势阱模型和深刻理解量子力学基本知识与原理有极大的帮助.我们处理的思路为其它类型无限深势阱模型的求解及非经典特性研究提供有价值的理论基础.

［1］P.A.M.Dirac.The Principles of Quantum Mechanics［M］.4thed.，Oxford University Press，1958.

［2］刘晓军.有限差分法解薛定谔方程与Matlab实现［J］.高师理科学刊，2013（3）：68－70.

［3］朱萧霄，崔艳波，丁鑫，等.有限差分法解薛定谔方程及其应用［J］.常州工学院学报，2014（4）：37－41.

［4］刘建军，翟利学.有限差分法解能量本征值方程［J］.北京工业大学学报，2008（3）：325－331.

［5］宫建平.有限差分法求解薛定谔方程［J］.晋中学院学报，2014（3）：1－6.

［6］陈皓，高明，汪青杰.用有限差分法解薛定谔方程［J］.沈阳航空工业学院学报，2005（1）：87－88.

［7］黄昆，韩汝琦.固体物理学［M］.高等教育出版社，1999.

［8］S.Datta.Quantum Transport：Atom to Transistor［M］.Cambridge University Press，2005.

Research on Quantum Properties of Particle Trapped in One－Dimensional Infinite PotentialWellwith Triangular On－Site Potential

XIANG Shao-hua，LAIQing-qing，CHEN Ying
（College of Electrical and Information Engineering，Huaihua University，Huaihua，Hunan 418008）

The equation ofmotion for wave function of a particle trapped in one－dimensional infinite potential well with a triangular on－site potential is solved numerically bymeans of the finite differencemethod.The effect of the on－site potential on the first few energy levels and the corresponding probability densities is discussed.It is shown that theminimum energies of the particle increasewith the increasing of the on－site potential，whereas their probabilitiesare completely different from each other in the spatial distribution.When increasing the on－site potential，the wave crest of the ground state probability density canmove to the left and that of the first excited state willmove to the opposite direction.For the second excited state，the increase of the centralwave－crest amplitude is observed and on the contrary，the wave crests in both sides are suppressed.

quantum mechanics；infinite potentialwell；triangular on－site potential；finite differencemethod

O413.1

A

1671－9743（2015）11－0035－04

2015－05－30

湖南省教育厅教改项目“基于创新素质培养为目标的物理学专业课程体系的构建与实践研究”（湘教通［2012］401号）；怀化学院教改课题“基于创新素质培养为目标的物理学专业课程体系的构建与实践研究”（201202）.

向少华，1972年生，男，湖南麻阳人，教授，博士，研究方向：物理学教学与科研.